Вариант № 863467. Задание 1 № 45. Решение.. Задание 2 № 85. Решение.. Задание 3 № 97. Задание 4 № 1241. Решение.. Задание 5 № 172. Решение.. Задание 6 № 187. Решение.. Примечание.

Вариант № 863467

ВПР-3

1. Задание 1 № 45

Найдите все двузначные числа, которые кратны 15 и одновременно не кратны 25. Сложите эти числа, затем умножьте полученную сумму на 7. В ответ запишите найденное произведение.

Решение.

Выпишем все двузначные числа, кратные 15: 15, 30, 45, 60, 75, 90.

Из них 25 кратно только 75.

Сложим оставшиеся числа: 15 + 30 + 45 + 60 + 90 = 240.

Умножим полученную сумму на 7: 240 · 7 = 1680.

Ответ: 1680

2. Задание 2 № 85

Сложите числа 20 и числа 18. В ответе напишите полученный результат.

Решение.

Найдем числа 20:

Найдем числа 18: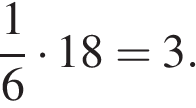

Получим: 12 + 3 = 15.

Ответ: 15

3. Задание 3 № 97

Запишите цифрами десятичную дробь: «ноль целых пятьдесят девять десятитысячных».

Ответ: 0,0059

4. Задание 4 № 1241

Две пятых всех учащихся класса составляют девочки. Сколько всего учащихся в этом классе, если в этом классе 18 мальчиков?

Решение.

Две пятых всех учащихся класса составляют девочки, следовательно, три пятых составляют мальчики.

Вычислим количество учащихся: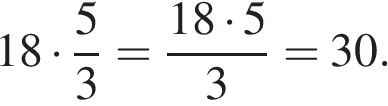

Ответ: 30

5. Задание 5 № 172

Найдите значение выражения

Решение.

Найдем значение выражения:

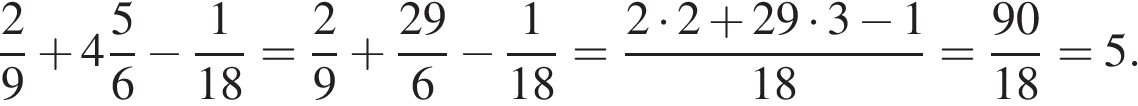
Ответ: 5.

6. Задание 6 № 187

В 6,5 кг свинины содержится 2,6 кг жиров. Сколько жиров содержится в 10,5 кг такой свинины?

Запишите решение и ответ.

Решение.

Выясним, сколько жиров будет содержаться в 1 кг свинины: 2,6 : 6,5 = 0,4 кг.

Найдем теперь, сколько жиров будет содержаться в 10,5 кг свинины: 0,4 · 10,5 = 4,2 кг.

Допускается другая последовательность действий, обоснованно приводящая к верному ответу.

Ответ: 4,2 кг.

Примечание.

Задачу можно решить, составив пропорцию: 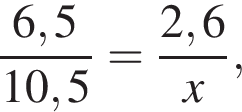где x — содержание жира в свинине. Таким образом: 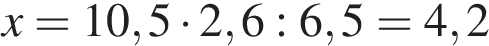кг.

7. Задание 7 № 225

На овощной базе 2 ц картофеля раскладывают в пакеты по 3 кг. Сколько килограммов картофеля осталось неупакованным?

Решение.

Переведем центнеры в килограммы: 2 ц = 200 кг.

Получим: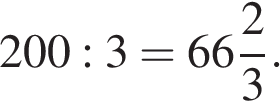

Осталось неупакованным: кг картофеля.

Ответ: 2

8. Задание 8 № 245

Применяя интенсивную технологию, бригада изготовила сверх плана 250 деталей, перевыполнив тем самым план на 5%. Сколько деталей изготовила бригада?

Решение.

Получим: 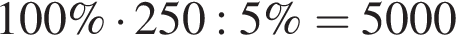деталей должна была изготовить бригада по плану. Таким образом, бригада изготовила деталей всего.

Ответ: 5250

9. Задание 9 № 289

Найдите значение выражения 30,3 · (124,9 − (48,96 : 6,8 + 36,04) : 9,2).

Запишите решение и ответ.

Решение.

1) 48,96:6,8=7,2

2) 7,2+36,04=43,24

3) 43,24:9,2=4,7

4) 124,9-4,7=120,2

5) 30,3*120,2=3642,06

Ответ: 3642,06.

10. Задание 10 № 310

В магазин привезли 250 коробок, в каждой коробке по 54 пачки печенья. Сколько денег выручит магазин от продажи этого печенья, если одна пачка печенья стоит 32 к.?

Запишите решение и ответ.

Решение.

Решение: Магазин получит прибыли:

к.

Ответ: 432000.

11. Задание 11.1 № 1328

На диаграмме показано, сколько раз в Большом театре шли балеты «Щелкунчик» и «Лебединое озеро» в течение пяти лет.

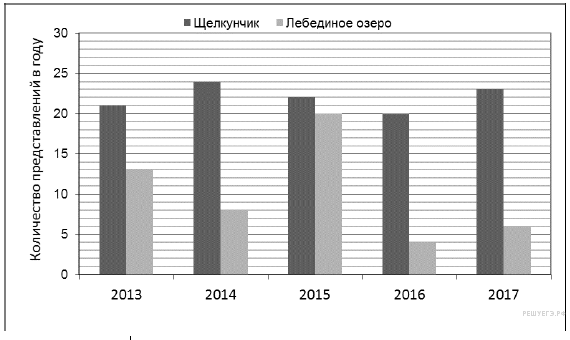
В каком году в Большом театре балет «Лебединое озеро» шёл меньше раз, чем в другие годы?

Решение.

Из диаграммы видно, что в 2016 году в Большом театре балет «Лебединое озеро» шёл меньше раз, чем в другие годы.

Ответ: 2016

12. Задание 11.2 № 468

На диаграмме показана средняя температура воздуха в Минске за каждый месяц 2003 года. По горизонтали указываются месяцы, по вертикали — средняя температура в градусах Цельсия. Используя диаграмму, ответьте на вопрос.

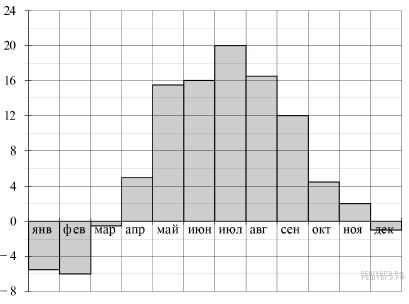
В каком месяце была самая низкая температура?

В ответе укажите одно слово — название месяца в именительном падеже.

Решение.

Самая низкая температура наблюдалась в феврале.

Ответ: февраль

13. Задание 12.1 № 417

На рисунке изображён план сада, вдоль периметра которого нужно вырыть канаву.

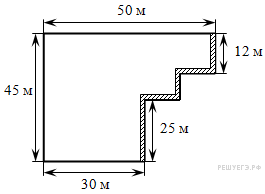
Какова будет длина канавы? Ответ дайте в метрах.

Решение.

Найдем длину канавы: 30 + 45 + 50 + 12 + (50 - 30) + (45 − 12 − 25) + 25 = 190 м.

Ответ: 190

14. Задание 12.2 № 528

На рисунке изображен план земельного участка.

Найдите площадь заштрихованной поверхности земельного участка.

Решение.

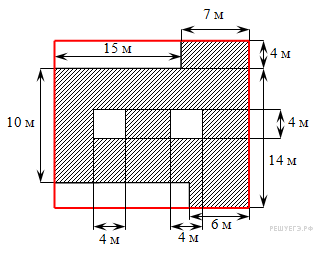
Найдём площадь как разность большого прямоугольника и четырех незаштрихованных (см. рис.):

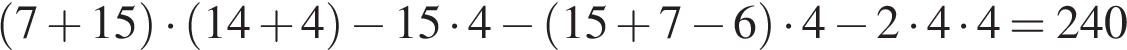м².

Ответ: 240.

15. Задание 13 № 360

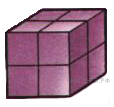
На рисунке показан куб, сложенный из 8 маленьких кубиков. Из скольки прямоугольных параллелепипедов можно составить такой куб?

Решение.

Данную фигуру можно рассматривать как составленную из двух или четырех прямоугольных параллелепипедов.

Примечание: в курсе стереометрии будет рассказано, что отдельный кубик является частным случаем прямоугольного параллелепипеда. Поэтому верным ответом будет также 1 и 8.

Ответ: 1, или 2, или 4, или 8.

Ответ: 1|4|2|8

16. Задание 14 № 387

Саша заметил, что когда он ехал в школу на автобусе, а возвращался на троллейбусе, то на весь путь было затрачено 35 мин. Когда же он туда и обратно ехал на автобусе, затратил 40 мин. Сколько времени потратит Саша на путь в школу и обратно, если будет ехать на троллейбусе?

Запишите решение и ответ.

Решение.

Пусть х — время, которое Саша тратит, когда едет на автобусе.

Тогда: минут едет автобус.

Следовательно: минут едет троллейбус.

Таким образом, на весь путь Саша потратит минут на троллейбусе.

Ответ: 30 минут.