Сделать рисунок 2 в тетрадь и записать формулу для вычисления площади поверхности прямоугольного параллелепипеда.

17.12.20. Математика. Тема урока «Прямоугольный параллелепипед».

1.Открываем тетрадь, записываем дату и тему урока.

2. Смотрим два видео урока по ссылкам, обращаем внимание на все элементы прямоугольного параллелепипеда, их обозначение, и решение задач. https://infourok.ru/videouroki/2926

https://znaika.ru/catalog/5-klass/matematika/Pryamougolnyy-parallelepiped

3. Внимательно читаем конспект урока изаписываем важную и нужную информацию в тетрадь, сделав чертеж. Советую внимательно сначала все прочитать, а затем работать письменно.

В тетради должен быть сделан рисунок, прямоугольный параллелепипед обозначен (как на рисунке 1), выписаны все шесть граней, все 8 вершин и все 12 ребер (подумайте как их удобно записать для запоминания и какие из них равны между собой).

У любого прямоугольного параллелепипеда есть 8 вершин. Зачастую их обозначают 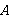, , 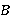, 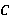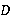снизу, 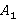, , 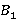, 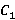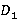– сверху. (Рис. 1.)

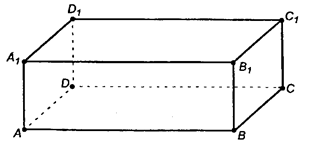
Рис. 1. Прямоугольный параллелепипед

6 прямоугольников, вершины которых совпадают с вершинами параллелепипеда, называются гранями:

· Передняя и задняя ,

· Верхняя 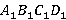и нижняя ,

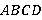· Левая 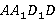и правая .

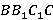На рисунке они не все выглядят как прямоугольники, это происходит потому что, мы смотрим на них не прямо, а под углом.

Еще есть отрезки АВ, В 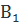, ВС и так далее. Они являются сторонами прямоугольников, то есть граней, и называются ребрами. У любого параллелепипеда 12 ребер.

Итак, у любого параллелепипеда всегда 8 вершин, 6 граней и 12 ребер.

Три ребра, исходящих из одной вершины, могут иметь разную длину. Пусть они будут обозначены

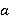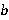, , и 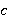. (Рис. 2.)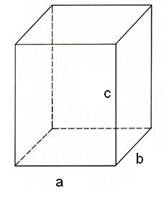

Рис. 2. Прямоугольный параллелепипед со сторонам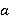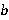и , , и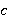

Сделать рисунок 2 в тетрадь и записать формулу для вычисления площади поверхности прямоугольного параллелепипеда.

Все остальные ребра равны какому-нибудь из этих значений. Необходимо найти площади всех граней и сложить.

Площадь нижней грани равна 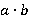, так это прямоугольник. Верхняя грань точно такая же, ее площадь тоже равна 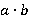. Правая и левая грани имеют площади 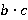каждая. Передняя и задняя – 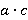каждая.

Складывая все эти площади, получаем площадь поверхности:

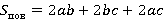
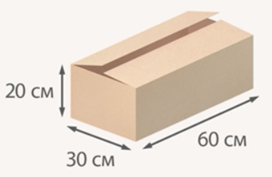
4.Задача. Сколько необходимо краски для покраски картонной коробки, если высота, ширина и длина коробки составляют 20, 30 и 60 см соответственно? Расход краски составляет 1 г на каждые 100 см².

Решение

Какую площадь надо покрасить? Очевидно, это площадь поверхности коробки, ведь красить мы будем ее поверхность.

Найдем площадь поверхности коробки. Коробка – это прямоугольный параллелепипед. Площадь поверхности – это сумма площадей всех граней, причем грани попарно равны.

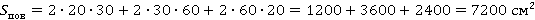
Расход краски – 1 г на 100 см². Чтобы найти необходимое количество краски, делим общую площадь на 100:

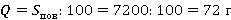
Получается, что необходимо 72 грамма краски, чтобы покрасить коробку.

Итак, сегодня на уроке был изучен прямоугольный параллелепипед, его основные свойства и элементы. Кроме того, была выведена формула его поверхности и решена задача на применение данной формулы.

5. Выполнить в тетради следующие задания письменно.

№ 796 – решить задачу по действиям.

№ 797 – решить задачу по действиям.

№ 817 – решить задачу по действиям.

6. Фото работ прислать в ВК 17.12.20. до 18:00. Стараемся все сделать во время нашего урока.