Федеральное агентство по образованию

Федеральное агентство по образованию

Государственное образовательное учреждение

высшего профессионального образования

ПЕРМСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ

Аналитическая геометрия

Индивидуальные задания

Пермь 2007

Образец решения варианта

Задача 1.Даны вершины треугольника: А (1,-3), В (2,5) и С (8,1). Найти точку пересечения медианы, проведенной из вершины А и высоты – из вершины В, а также длину медианы, проведенной из вершины А.

Решение:

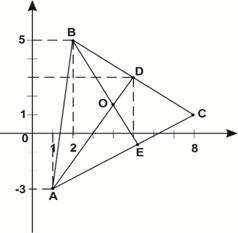
Рис. 1

Составим уравнение медианы АD. Координаты точки D определяем по формулам координат середины отрезка 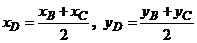. 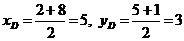D (5; 3). Используем уравнение прямой, проходящей через две точки . Получаем .

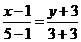Уравнение медианы AD: .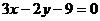

Составим уравнение высоты, проведенной из вершины В. Так как ВЕ ^ АС, следовательно 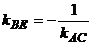. Угловой коэффициент прямой АС определяем по формуле 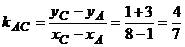. Следовательно, . Используем уравнение прямой, проходящей через данную точку М₀ (x₀,y₀) в данном направлении .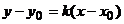

Уравнение высоты из вершины В: , .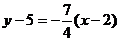

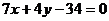Для нахождения координат точки пересечения медианы, проведенной из вершины А и высоты, проведенной из вершины В нужно решить совместно из уравнения 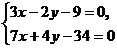. Точка О (4; ).

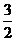Длина медианы определяется по формуле расстояния d между точками А (x₁,y₁)и D (x₂,y₂) на плоскости .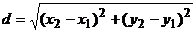

А (1,-3), D (5,3) .

Задача 2.Составить уравнения прямых, проходящих через начало координат и образующих с прямой .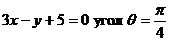

Решение:

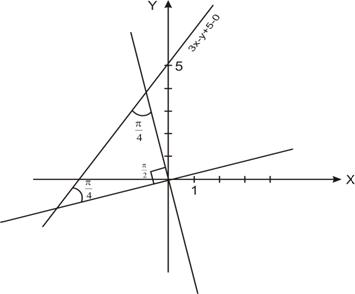
Рис. 2

Уравнения искомых прямых имеют вид 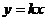, так как прямые проходят через начало координат. Задача имеет два решения (Рис. 2). Для решения используем формулу 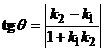, причем, поскольку нас интересует острый угол, правую часть формулы возьмём по абсолютной величине. Пусть угловой коэффициент одной из искомых прямых равен k. Угловой коэффициент заданной прямой равен 3. Так как угол между этими прямыми равен 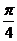, то .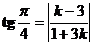

Тогда 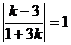, отсюда 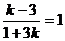и .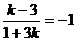

Решая каждое из получившихся уравнений, находим, что угловой коэффициент одной из прямой 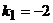, а другой 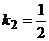. Уравнения искомых прямых .

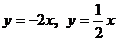Задача 3.Даны вершины А (-3,-2), В (4,-1), С (1,3) трапеции ABCD (AD || BC). Составить уравнение средней линии трапеции. Полученное уравнение привести к уравнению в «отрезках» и к нормальному.

Решение: Составим уравнение прямой ВС (уравнение прямой, проходящей через две точки).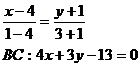

От общего уравнения прямой ( 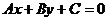) перейдем к уравнению с угловым коэффициентом ( ).

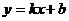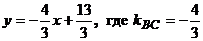
Средняя линия трапеции параллельна ВС и проходит через середину отрезка АВ. Е – середина АВ, следовательно Е ( ).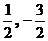

Так как прямые параллельны, то 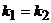. Используем уравнение прямой

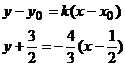
Уравнение средней линии трапеции: .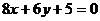

Уравнение прямой в отрезках:

Рис. 3

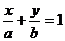, а – величина отрезка отсекаемого прямой на оси ОХ, b - величина отрезка отсекаемого прямой на оси ОY.

Перенося свободный член данного уравнения в правую часть равенства, получим 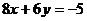. Деля обе части равенства на -5, будем иметь 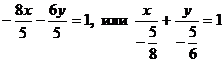. Следовательно, (Рис. 4).

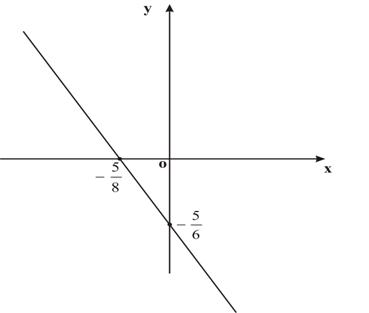
Рис. 4

Нормальное уравнение прямой (Рис. 5) 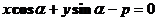, р – длина перпендикуляра, опущенного из начала координат на прямую, a - угол, который образует этот перпендикуляр с положительным направлением оси ОХ.

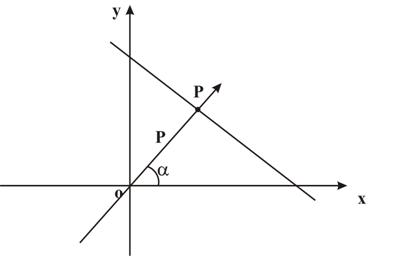
Рис. 5

Для приведения общего уравнения прямой к нормальному виду обе его части надо умножить на нормирующий множитель 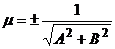, причем перед дробью следует выбрать знак, противоположный знаку свободного члена С в общем уравнении прямой.

Находим нормирующий множитель 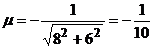(знак минус берется потому, что С = 5 > 0). Таким образом, нормальное уравнение полученной прямой имеет вид .

Направляющие косинусы 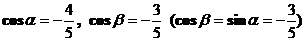. Длина перпендикуляра из начала координат к прямой .

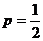Задача 4. Найти расстояние между параллельными прямыми .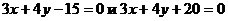

Решение: Искомое расстояние найдем как расстояние от произвольной точки первой прямой до второй прямой. Возьмем на первой прямой произвольную точку, например, точку с абсциссой 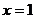. Её ордината 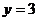. Итак, на первой прямой выбрана точка А (1;3). Найдем теперь расстояние этой точки до второй прямой по формуле .

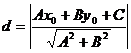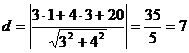Задача 5.Даны точки М₁ (-3; 7; -5) и М₂ (-8; 3; -4). Составить уравнение плоскости, проходящей через точку М₁ и перпендикулярной вектору .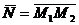

Решение: Найдем координаты нормального вектора 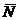. Имеем .

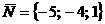Уравнение плоскости, проходящей через данную точку М ( 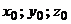). Перпендикулярно данному вектору : .

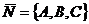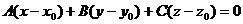Искомое уравнение плоскости: .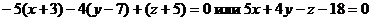

Задача 6.Через точку пересечения плоскостей 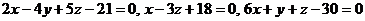провести плоскость, параллельную плоскости . Найти расстояние точки М₁ (1; -1; -1) до построенной плоскости.

Решение:

Плоскости пересекаются, следовательно 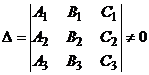. Решив систему уравнений 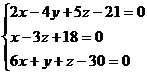, получим точку М (3; 5; 7).

Так как искомая плоскость параллельна плоскости 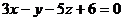, то в качестве ее нормального вектора можно взять нормальный вектор 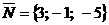данной плоскости ( 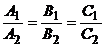- условие параллельности двух плоскостей).

Используя теперь уравнение плоскости, проходящей через точку М перпендикулярно данному вектору 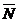, получаем 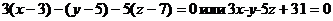. Это и есть искомое уравнение.

Расстояние от точки 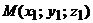до плоскости 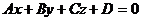определяется по формуле 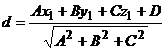. В данном случае .

Задача 7.Плоскость a проходит через точки: 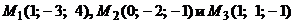. Плоскость b проходит через ось ОХ и точку 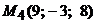. Найти угол между плоскостями a и b.

Решение: Уравнение плоскости, проходящей через три данные точки 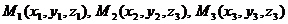имеет вид 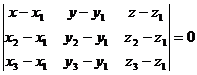. В данном случае .

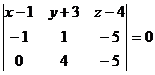Раскрывая этот определитель, получим 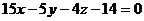- уравнение плоскости a. Если плоскость проходит через ось ОХ, А = 0, D = 0(общее уравнение плоскости 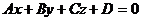) т. е. 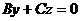. Плоскость b проходит через ось ОХ и точку М₄ (9,-3, 8). Подставляем в это уравнение координаты точки М₄ получим 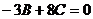или 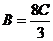, таким образом, имеем 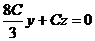, т. е. - уравнение плоскости b.

Угол между плоскостями определяется по формулам 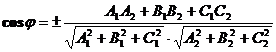, где 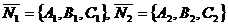. Нормальный вектор плоскости a: 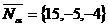. Для плоскости b: 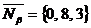. Определяем острый угол между плоскостями a и b: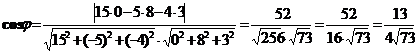

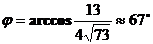Задача 8.Общее уравнение прямой 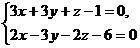преобразовать к каноническому виду.

Решение:

Первый способ. Наметим такой план решения задачи: из системы исключим сначала y и выразим z через x, потом исключим х и выразим z теперь уже через y.

Для того чтобы из системы исключить у, сложим первое уравнение системы почленно со вторым. Получим, что 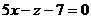, откуда .

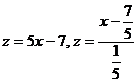Умножая первое уравнение на (2), а второе на ,(-3) и складывая их почленно, получим 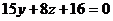, откуда 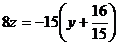или .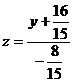

Сравнивая найденные значения z, получаем уравнение прямой в каноническом виде .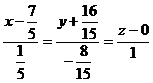

Умножая теперь все знаменатели на 15, окончательно получим 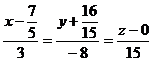. Прямая проходит через точку 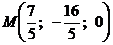и имеет направляющий вектор .

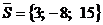Второй способ. Найдем направляющий вектор 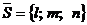прямой. Так как он должен быть перпендикулярен нормальным векторам заданных плоскосте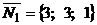й и 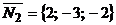, то в качестве его можно взять векторное произведение векторов : .

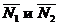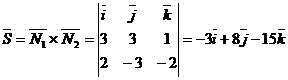Таким образом, l = -3, m = 8, n = -15. За точку , через которую проходит искомая прямая, можно принять точку её пересечения с любой из координатных плоскостей, например с плоскостью ХOY. Поскольку при этом , координаты определяются из системы уравнений заданных плоскостей, если положить в них

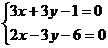, отсюда получаем 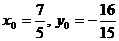. Так как каноническое уравнение имеет вид 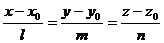, то в данном случае .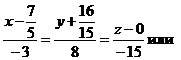

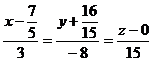Задача 9.Написать уравнение прямой l, проходящей через точки А (-1; 2; 3) и В (5; -2; 1). Лежат ли на этой прямой точки: К (-7; 6; 5), L (2; 0; 1), М (-4; 4; 4)? При каком значении m прямая l перпендикулярна прямой .

Решение: Уравнение прямой, проходящей через две данные точки М (х_1;y₁; z₁) и N(x₂; y₂; z₂):

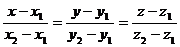
Прямая l: . Подставляем в эти уравнения координаты точек K, L, M, соответственно находим: 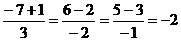; ; 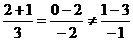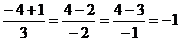. Следовательно, KÎl, MÎl, LÏl. Условие перпендикулярности двух прямых - 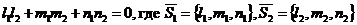. В данном случае для прямой .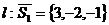

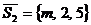Тогда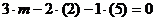

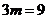
При 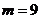прямые перпендикулярны.

Задача 10.При каких значениях n и А прямая 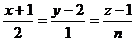и плоскость 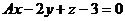будут перпендикулярны? При n = -1 и А = 3 найти точку пересечения прямой с плоскостью и угол между ними.

Решение: 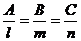- условие перпендикулярности прямой и плоскости (Рис. 6).

Рис. 6

В данном случае

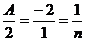
При А = -4; n = 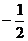прямая и плоскость перпендикулярны.

Если n = -1, то прямая имеет вид .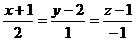

Если А = 3, то плоскость имеет вид .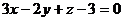

Запишем уравнение прямой в параметрическом виде: 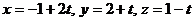. Подставляя значения x, y, z в уравнение плоскости, имеем 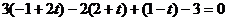, откуда 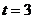. Подставляя теперь это значение t в параметрические уравнения прямой, находим координаты точки пересечения: 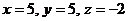, М (5; 5; -2).

Острый угол между прямой 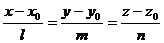и плоскостью 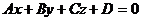определяется по формуле 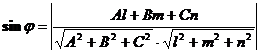. Учитывая, что 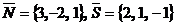получаем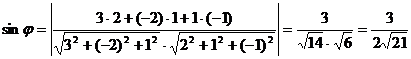

Задача 11.Дана прямая и вне её точка М (1; 1; 1). Найти точку N, симметричную М относительно данной прямой.

Решение: Проведем через М плоскость a, перпендикулярную к данной прямой. a: 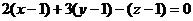или .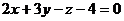

Найдем точку Q, где эта плоскость пересекает данную прямую. Запишем уравнение прямой в параметрическом виде: 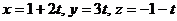. Подставляя x, y, z в уравнение плоскости, получим 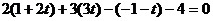, отсюда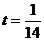

Точка Q имеет координаты 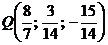. Тогда координаты симметричной точки можно найти из формулы координат середины отрезка, т. е. 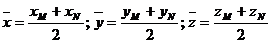или . Откуда 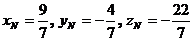. Следовательно, .

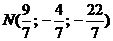Вариант 1

1. Проверить, является ли прямоугольным треугольник с вершинами А (4; -5), B (7; 6) и С (-7; -2). Составить уравнения его сторон.

2. Через точку пересечения прямых провести прямую, составляющую с осью ОХ угол 45°.

3. К какой из двух прямых: 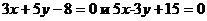точка М(-1;2) находится ближе?

4. Показать, что отрезки прямых 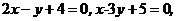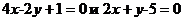образуют трапецию. Найти внутренние углы трапеции.

5. Дан тетраэдр с вершинами А(1; 3; 6), В (2; 2; 1), С (-1; 0; 1) и В (-4; 6; -3). Найти длину высоты, проведенной из вершины А, и угол между гранями ВСD и АСВ . Составить уравнение плоскости, проходящей через вершину А параллельно грани BCD.

6. Плоскость проходит через точку M (1; -3; 5) и отсекает на осях ОY и OZ вдвое большие отрезки, чем на оси ОX. Вычислить направляющие косинусы прямой, перпендикулярной к этой плоскости.

7. Составить уравнение плоскости, проходящей через ось Ох перпендикулярно к плоскости .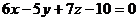

8. Написать канонические уравнения прямой: .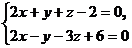

9. Найти точку пересечения прямой 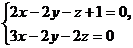с плоскостью 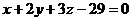и угол между ними.

10. Дан треугольник с вершинами А (7; 2; -6), В (11; -3; 5), С (-3; 4; -2). Составить уравнение медианы, проведенной из вершины В. При каком значении m прямая 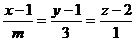будет перпендикулярна построенной прямой?

11. Проверить, лежит ли прямая 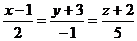на плоскости .

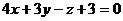Вариант 2

1. Написать уравнения высот треугольника, вершины которого находятся в точках К (2; 5), А. (-4; 3), М (6; -2).

2. Найти угол наклона к оси ОХ и начальную ординату прямой 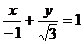. Построить данную прямую.

3. Найти расстояние между параллельными прямыми .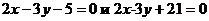

4. Даны уравнения сторон треугольника: 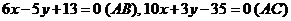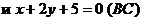. Определить угол между медианами, проведенными из вершин А и В.

5. Плоскость a проходит через точки А (-1; 3; 4), B (-1; 5; 0) и C (2; 6; 1), плоскость b задана уравнением 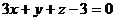. Показать, что плоскости перпендикулярны, и выяснить, какая из них расположена ближе к началу координат.

6. Через точку M (-5; 16; 12) проведены две плоскости: одна из них содержит ось OX, другая - ОY . Вычислить угол между этими плоскостями.

7. Через точку М (2; 3; -1) провести плоскость, параллельную плоскости 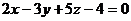. Составить для построенной плоскости уравнение в "отрезках".

8. Написать канонические уравнения прямой: .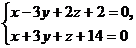

9. Составить уравнения прямой, которая проходит через точку А (1; -5; 3) и образует с осями координат ОХ и OY углы, соответственно равные 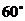и 45^°, а с осью OZ – тупой угол.

10. Показать, что прямые взаимно перпендикулярны.

11. При каком значении А плоскость 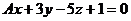будет параллельна прямой 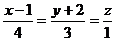. При А = 4 найти угол между ними.

Вариант 3

1. В параллелограмме АВСD даны вершины А (-1; 3), В (4; 6) и С (1;-5). Составить уравнения его сторон.

2. Какая зависимость существует между а и b , если угол наклона прямой 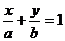к оси OX равен 45° ?

3. Найти длину перпендикуляра, опущенного из начала координат на прямую 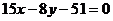, и угол, образованный этим перпендикуляром с осью ОУ.

4. Дан треугольник с вершинами: А (-3; -5), В (9; 1) и С (-3; 5). Определить координаты точки пересечения и острый угол между медианой, проведенной из вершины А, и высотой, проведенной из вершины С на сторону АВ.

5. Плоскость a проходит через точки А (-1; 10; -3), (1; 1; -5) и С (5; 4; -2), плоскость b проходит через точку М (2; -3; -9) и отсекает на осях ОХ и ОУ отрезки а = 18, b = 27. Показать, что плоскости параллельны, и найти расстояние между ними.

6. Написать уравнение плоскости, проходящей через точку М (-3; 1; 2) параллельно векторам 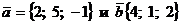. Найти угол между построенной плоскостью и плоскостью .

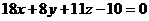7. Нормаль к плоскости составляет с координатными осями ОХ и ОУ угол a = 150° и b = 120°. Составить уравнение плоскости при условии, что расстояние Р от начала координат до неё равно 5 ед. Указать особенность в расположении плоскости.

8. Написать канонические уравнения прямой: .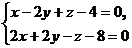

9. Найти острый угол между прямыми, одна из которых задана уравнением 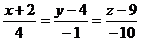, другая проходит через точки А (2; -5; 3) и В (13; 2; -5).

10. При каких значениях В и n прямая 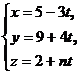перпендикулярна плоскости ?

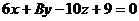11. Составить уравнение прямой, проходящей через точку М (-4; -7; 1) и параллельно прямой .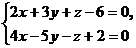

Вариант 4

1. В треугольнике АBС известны вершины А(-3; -4), В(1; -2) и С(7; -2). Составить уравнения средней линии, параллельной АС, и медианы, проведенной из вершины В.

2. Составить уравнение прямой, если известно, что она проходит через точку A(-1; 4) параллельно прямой .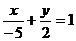

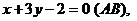
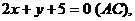
3. Стороны треугольника выражаются уравнениями 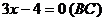. Найти уравнение высоты, опущенной из вершины B на сторону АСи её длину.

4. Через начало координат провести прямые, образующие с прямой 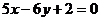углы, тангенсы которых равны .

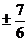5. Написать уравнение плоскости, параллельной оси ОХ и проходящей через точки М (0; 1; 3) и N (2; 4; 5), и построить её. Найти расстояние точки А (3; 2; -5) до построенной плоскости.

6. При каком значении l плоскости a и b будут перпендикулярны? Плоскость a проходит через точки К (-1; 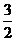; 0), М (2; -1; 1), N (8; 1; -1). Плоскость b задана уравнением 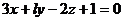. При l = 3 найти острый угол между плоскостями a и b.

7. Написать уравнение плоскости, проходящей через точку М (-2; 7; 3) параллельно плоскости 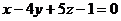. Полученное уравнение плоскости привести к нормальному виду.

8. Написать канонические уравнения прямой: .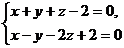

9. Найти угол между прямым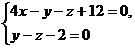и и .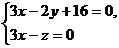

10. Даны вершины четырехугольника: A (-4; -3; -2), B (2; -2; -3), C (-8; -5; 1), D (4; -3; -1). Доказать, что его диагонали взаимно перпендикулярны.

11. Найти значение m, при котором прямая 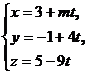параллельна плоскости 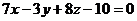. При m = -2 найти точку пересечения прямой с плоскостью.

Вариант 5

1. Даны вершины треугольника: А (4; 6), В (-4; 0) и С (-1; -4). Составить уравнения высоты, опущенной из вершины А на сторону BС, и медианы, проведенной из вершины С.

2. Найти площадь треугольника, заключенного между осями координат и прямой .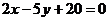

3. Дана прямая 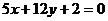. Найти уравнение прямой, параллельной данной и отстоящей от неё на расстоянии 3 единиц.

4. Найти острый угол между прямой 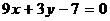и прямой, проходящей через точки А (1; -1) и В (5; 7).

5. На оси ОX найти точку, удаленную от плоскости, проходящей через точку М (1; 8; -1) перпендикулярно вектору , на расстояние .

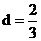6. Найти угол между плоскостями a и b, где a проходит через точки A (1; 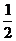; 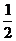), В (2; 0; 1) параллельно оси OZ , а b - через точки С (2; 2; 1), D (6; 1; 0) и E (-1; -1; 3).

7. Составить уравнение плоскости, проходящей через начало координат перпендикулярно вектору 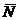, направляющие косинусы которого соответственно равны 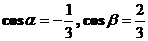. Проверить, будет ли искомая плоскость перпендикулярна плоскости .

8. Написать канонические уравнения прямой: .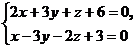

9. Найти угол между прямой 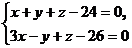и плоскостью .

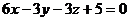10. Найти проекцию точки М (-6; 5; 7) на прямую .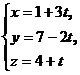

11. Доказать, что четырехугольник с вершинами A (3; 2; -3), B (2; 4; 6), C (8; 3; 4), D (9; 1; -5) есть параллелограмм. Найти длины его сторон.

Вариант 6

1. Даны вершин треугольника: А (2; -1), В (4; 5) и С (-3; 2). Составить уравнения высоты, опущенной из вершины В на сторону АС, в медианы, проведенной из вершины А.

2. Через точку А(1; 2) провести прямую, отсекающую на положительных полуосях координат равные отрезки.

3. Найти длину перпендикуляра, проведенного из начала координат к прямой 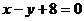, и угол, образованный этим перпендикуляром с осью ОХ .

4. Проверить, что прямые 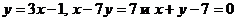служат сторонами равнобедренного треугольника.

5. Нормаль к плоскости составляет с координатными осями ОY и OZ углы b = 60° и g = 45°, а с осью ОХ - тупой угол. Составить уравнение плоскости при условии, что расстояние р от начала координат до неё равно 8 единицам. Найти расстояние от точки A (1; -1; 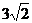) до построенной плоскости.

6. Определить объем тетраэдра, ограниченного координатными плоскостями и плоскостью a, проходящей через точки А (0; 4; 1), B (6; 2; 0), С (3; 0; 2). Найти угол между плоскостью a и плоскостью XОY.

7. Показать, что параллелепипед, грани которого лежат в плоскостях 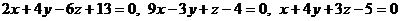является прямоугольным.

8. Написать канонические уравнения прямой: .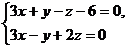

9. Найти точку пересечения прямой 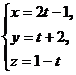с плоскостью 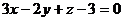и угол между ними.

10. Написать уравнение плоскости, проходящей через точку М (-3; 5; -1) и перпендикулярно прямой .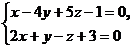

11. Точки A (-4; 3; 7), B (2; -1; 5) и C (-2; -6; 11) являются тремя вершинами параллелограмма. Составить уравнение стороны CD.

Вариант 7

1. Даны вершины треугольника: А (-1; 2), В (3; -1) и С (0; 4). Через каждую из них провести прямую, параллельную противолежащей стороне.

2. Прямая проходит через точку А(-1; -9) и отсекает на отрицательной полуоси абсцисс отрезок, вдвое меньший, чем на отрицательной полуоси ординат. Составить уравнение этой прямой.

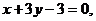
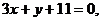
3. Известны уравнения сторон треугольника: 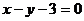. Найти длину высоты, которая проведена из вершины, лежащей на оси абсцисс.

4. Даны вершины четырехугольника: А (-9; 0), В (-3; 6), С (3; 4) и D (6; -3). Вычислить угол между диагоналями АС и ВD.

5. Две из граней куба расположены на плоскостях 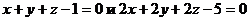. Найти его объем.

6. Найти угол между плоскостью 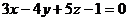и плоскостью, проходящей через точки М (1; 1; 1) и N (2; 3; -1) параллельно вектору 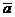={0; -1; 2}.

7. Составить уравнение плоскости АВС, где А (-3; -3; 1), В (-4; -2; -2), С (-5; -1; 0), и указать особенность в её расположении. Найти углы, образуемые перпендикуляром, опущенным из начала координат к плоскости, с координатными осями.

8. Написать канонические уравнения прямой: .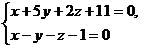

9. Найти угол прямой 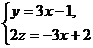с плоскостью .

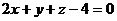10. При каком значении n прямые 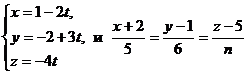будут взаимно перпендикулярны?

11. Вершины четырехугольника находятся в точках A (-3; -5; -1), B (2; -20; 9), C (-6; 1; -2), D (-9; 10; -8). Показать, что ABCD есть трапеция и найти длины её оснований.

Вариант 8

1. Проверить, что четыре точки: А (-2; -2), B (-3; 1), С (7; 7) и D (3; 1) служат вершинами трапеции, и составить уравнение средней линии трапеции.

2. Какая зависимость существует между а и b , если угол наклона прямой 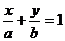к оси ОX равен 30° ?

3. Через точку пересечения прямых 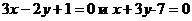проведена прямая перпендикулярно первой из данных прямых. Каково расстояние полученной прямой от начала координат?

4. Определить острый угол, под которым пересекаются прямые АВ и СD, если А (2; 4), В (4; 8), С (8; 3) и D (10; -2).

5. Составить уравнения плоскостей, параллельных плоскости 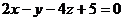и отстоящих от точки А (1; 2; 0) на расстоянии .

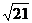6. Найти угол между плоскостью, проходящей через точку M (3; 6; -2) и отсекающей на осях координат отрезки, связанные соотношением а: в : с =1:3:2, и плоскостью XOZ.

7. Составить уравнение плоскости, проходящей через ось ОУ перпендикулярно к плоскости, проходящей через точки А (0; 2; 0), В ( 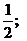0; 1) и С ( ).

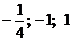8. Написать канонические уравнения прямой: .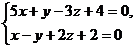

9. Составить уравнения прямой, проходящей через точки пересечения плоскости 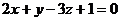с прямыми 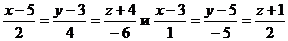. Определить направляющие косинусы прямой.

10. При каком значении m прямые 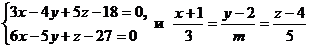будут взаимно перпендикулярны? При m = 1найти угол между ними.

11. Написать уравнение плоскости, которая проходит через точку М (3; 1; -2) и прямую .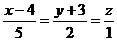

Вариант 9

1. Даны вершины треугольника: А (3; 0), В (0; 3) и С(-2; -1). Составить уравнение высоты, опущенной из вершины С на сторону АВ, и найти её длину.

2. Из пучка прямых а центром в точке О(2; -5) выбрать прямую, отсекающую на положительной полуоси ординат отрезок, равный 3 единицам. Полученное уравнение прямой привести к нормальному виду.

3. Найти прямую, проходящую через точку пересечения прямых 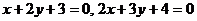и параллельную прямой .

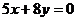4. Найти уравнение прямой, проходящей через точку. М (-4; 1)и образующей угол с прямой .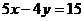

5. Найти расстояние от точки пересечения плоскостей 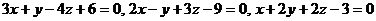до плоскости, проходящей через точку М (-1;-1; 1) перпендикулярно вектору .

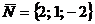6. Дан тетраэдр с вершинами А (1; -2; 2), В (2; -3; -6),С (5; 1; 4) и D (0; -4; 4). Найти угол между гранями ABD и BCD.

7. Плоскость a проходит через точку М (-5; 4; 13) и отсекает на осях координат равные отрезки. Плоскость b задана уравнением, 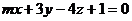. При каком значении m плоскости a и b будут перпендикулярны?

8. Написать канонические уравнения прямой: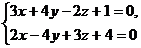

9. Даны две вершины параллелограмма ABCD: С (-2; 3; -5) и D (0; 4; -7) и точка пересечения диагоналей M (1,2,-3; 5). Найти уравнение стороны AB и угол между диагоналями AC и BD.

10. При каких значениях В и С прямая 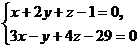перпендикулярна плоскости ?

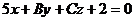11. При каких значениях А и С прямая лежит в плоскости ?

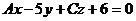Вариант 10

1. Вершины четырехугольника имеют координаты Р(1; 0), Q(2; 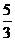), R(5; 2) и S(6; -1). Найти точку пересечения его диагоналей.

2. Диагонали ромба равны 8 и 3 единицам. Написать уравнения сторон ромба, если большая диагональ лежит на оси ОХ, а меньшая - на оси ОУ . Вычислить расстояние между параллельными сторонами этого ромба.

3. Составить уравнение перпендикуляра, восстановленного в середине отрезка, соединяющего точки М(-1; 7) и N(3; -1). Какой угол образует он с положительным направлением оси ОХ?

4. Вычислить угол между прямыми .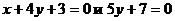

5. Составить уравнение плоскости, проходящей через точку А (1; 0; -2) перпендикулярно вектору 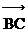, где В (2; -1; 3), С (0; -3; 2). Указать особенности в расположении плоскости. Найти расстояние от точки D (6; -2; 13) до построенной плоскости.

6. При каком значении m угол между плоскостями a и b равен 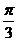? Плоскость a проходит через точки А ( 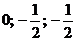), В (-3; 1; 1) и С (2; 4; -7), плоскость b задана уравнением .

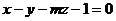7. Найти уравнение плоскости, проходящей через точки М (1; -1; 2), N (3; 1; -2) и перпендикулярной к плоскости ХОY.

8. Написать канонические уравнения прямой: .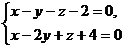

9. Составить канонические и параметрические уравнения прямой, проходящей через точку М (1; 2; 3), если направляющий вектор 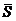прямой образует с координатными осями ОХ и OZ углы a = 120°, g = 45°, а с осью ОY - острый угол.

10. В плоскости XOZ найти прямую, проходящую через начало координат и перпендикулярную к прямой .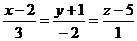

11. При каком значении С плоскость 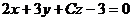будет параллельна прямой 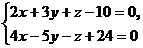. При С = -2 найти угол между ними.

Вариант 11

1. Показать, что точки M(4; 3), N (5; 0), Р (-5; -6) и Q (-1; 0) являются вершинами трапеции. Найти уравнение высоты трапеции, её длину.

2. Найти угол наклона к оси ОХ .и начальную ординату прямой .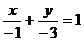

3. Определить, какие из уравнений прямой являются нормальными:

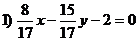
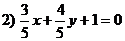
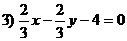
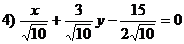
4. Найти вершины прямоугольного равнобедренного треугольника, если даны вершина прямого угла С(3; -1) и уравнение гипотенузы .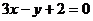

5. Найти такое число a, чтобы плоскость 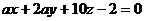была параллельна плоскости 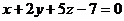, и определить расстояние между ними.

6. Построить линии пересечения координатных плоскостей с плоскостью a, проходящей через точки А(1; 1; -1), В(3; -1; 1) и С(2; 3; 2), Найти угол между плоскостью a и плоскостью XOZ.

7. Написать уравнение плоскости, проходящей через точку М(1; 1; 1) параллельно векторам 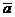={0; 1; 2} и 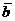= {-1; 0; l}.Указать особенность в расположении плоскости.

8. Написать канонические урав