
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Интегрирование по частям.
§6 Интегрирование по частям.
Теорема1. Пусть функции 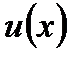 и
и 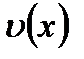 непрерывные на некотором промежутке, дифференцируемые внутри его и на этом промежутке существует интеграл
непрерывные на некотором промежутке, дифференцируемые внутри его и на этом промежутке существует интеграл 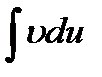 , тогда на нем существует и интеграл
, тогда на нем существует и интеграл 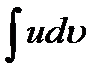 , причем
, причем 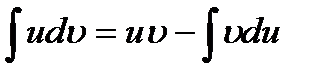 (1)
(1)
Доказательство:
Пусть функции 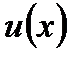 ,
, 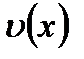 имеют непрерывные производные на некотором промежутке. Тогда функция
имеют непрерывные производные на некотором промежутке. Тогда функция 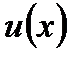

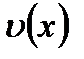 имеют непрерывную производную на этом же промежутке и согласно правила дифференцирования произведения, выполняется равенство:
имеют непрерывную производную на этом же промежутке и согласно правила дифференцирования произведения, выполняется равенство:
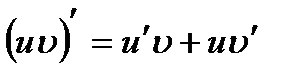 .
.
Отсюда следует, что произведение 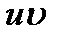 - первообразная для
- первообразная для 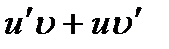 . Тем самым
. Тем самым
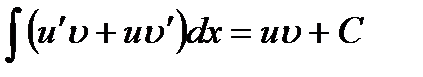 ,
,
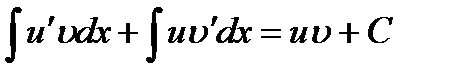 ,
,
Откуда 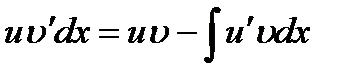 , т.к.
, т.к. 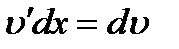 и
и  , то
, то 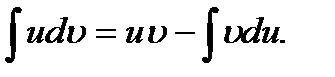
ПостояннуюС в правой части равенства мы не пишем, т.к. туда входит (1) интеграл, а он уже содержит в себе произвольную постоянную.
Замечание 1. Формула (1) есть формула интегрирования по частям . К числу интегралов которые вычисляются интегрированием по частям, относятся, например, интегралы вида 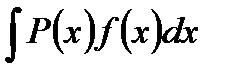 ,
, 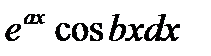 ,
, 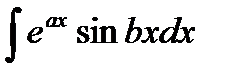 ; где P(x)-многочлен, f(x)- одна из следующих функций:
; где P(x)-многочлен, f(x)- одна из следующих функций: 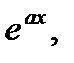
sinax, cosax, lnax, arctgax, arccosax,  .
.
В принципе всегда подынтегральное выражение любого интеграла можно разбить на 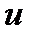 и
и 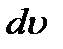 . Поэтому ясно, что формула интегрирования по частям дает эффект тогда, когда
. Поэтому ясно, что формула интегрирования по частям дает эффект тогда, когда 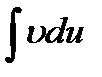 вычислить проще, чем
вычислить проще, чем 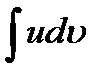 . При этом нужно иметь в виду , что, зная
. При этом нужно иметь в виду , что, зная 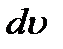 , нужно суметь найти
, нужно суметь найти 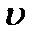 . При нахождении
. При нахождении 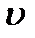 по
по 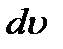 можно считать, чтоС = 0.
можно считать, чтоС = 0.
Примеры.
1) 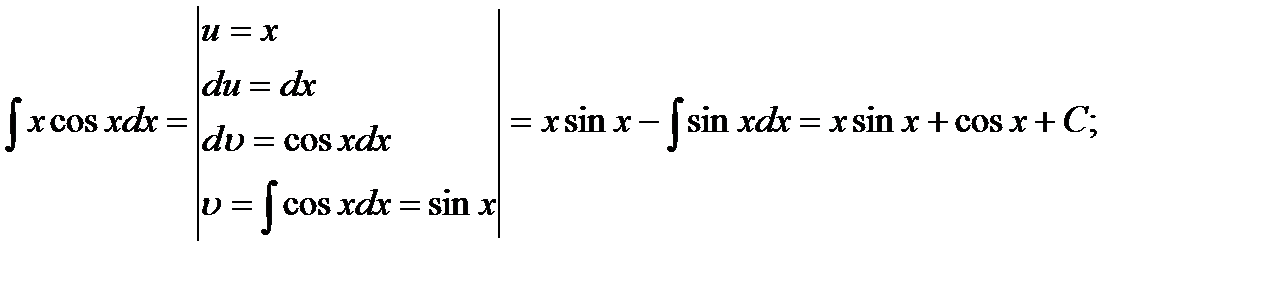
2) 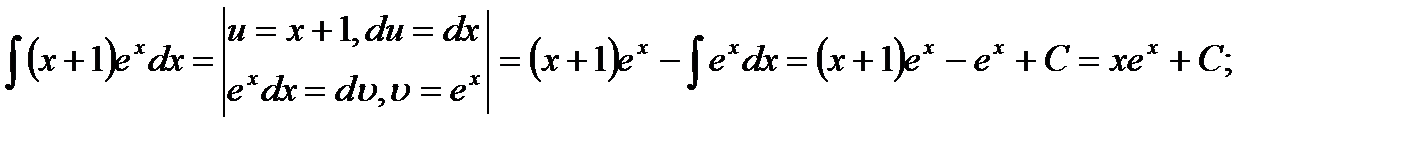
3) стр.13-14 №30-32
4) стр.13 №30
5) стр.13 №31 (голубое пособие)
6) 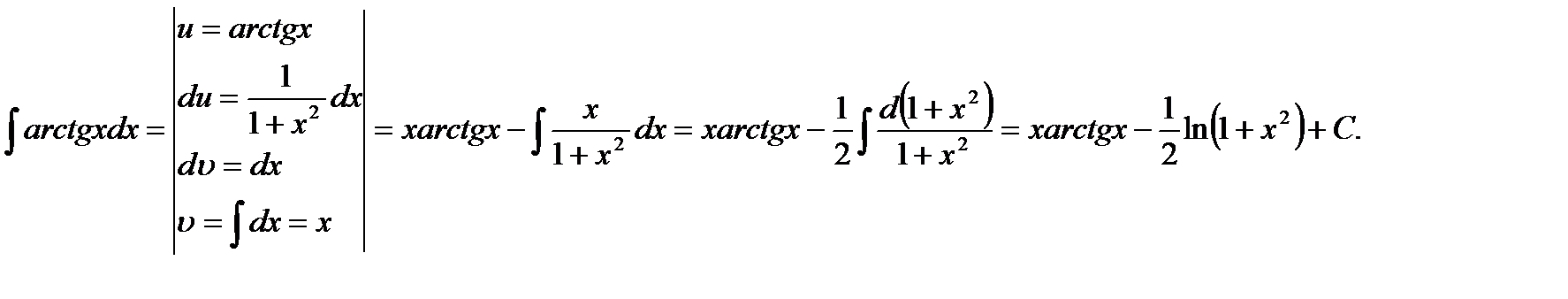
Иногда формулу интегрирования по частям применяют несколько раз.
Примеры
7) стр.14 №32
8) 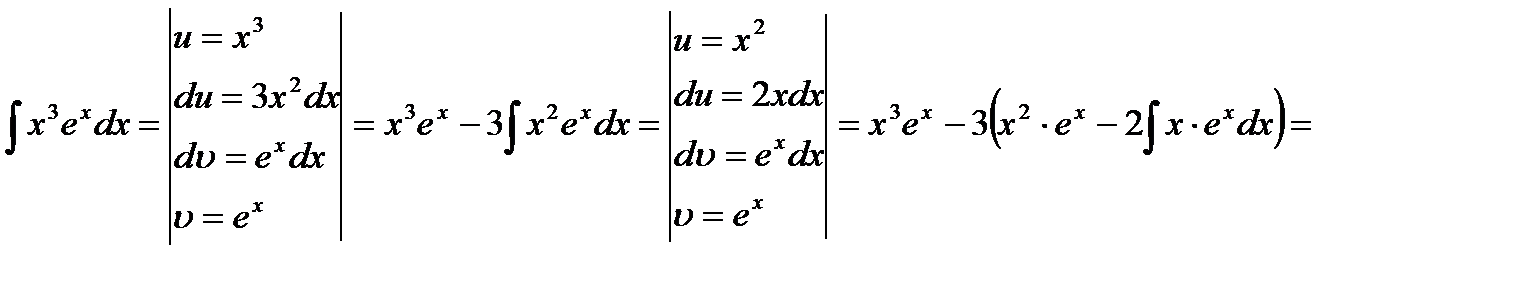
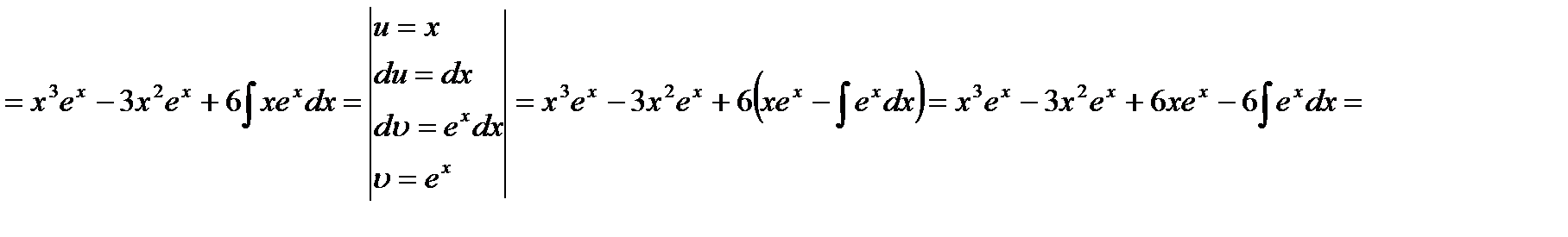
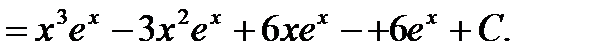
Если после применения формулы интегрирования по частям окажется, что интеграл 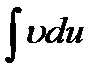 взять труднее, чем данный интеграл
взять труднее, чем данный интеграл 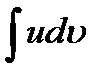 , нужно разбить подынтегральное выражение на
, нужно разбить подынтегральное выражение на 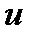 и
и 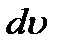 иначе и вновь применить формулу интегрирования по частям.
иначе и вновь применить формулу интегрирования по частям.
Иногда бывает, что интегрирование по частям приведет вновь к исходному интегралу. В этом случае интегрирование следует прекратить и решить линейное уравнение относительно искомого интеграла.
Примеры.
8) 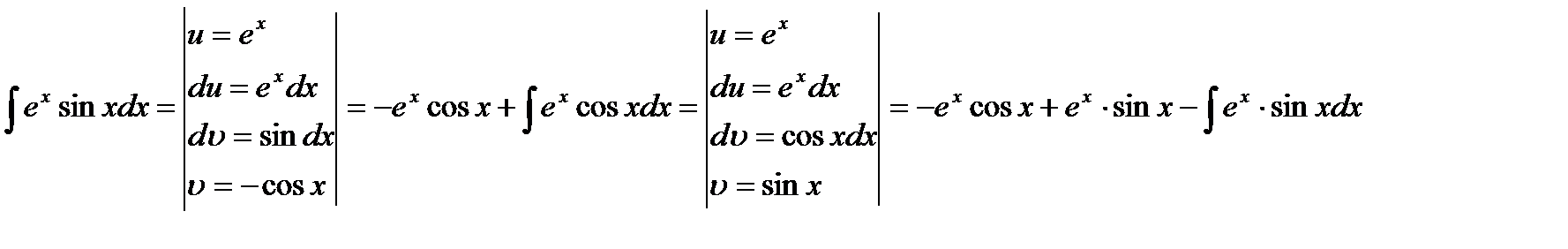
Итак, получили:
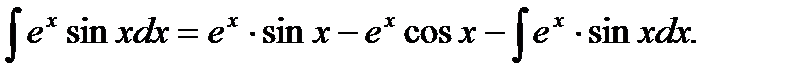
Решаем уравнение относительно искомого интеграла.
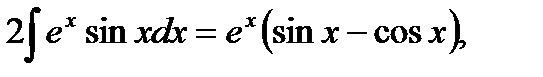
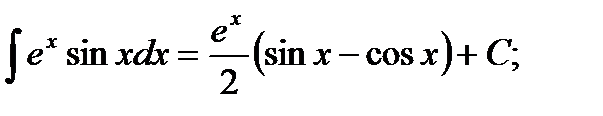
9) 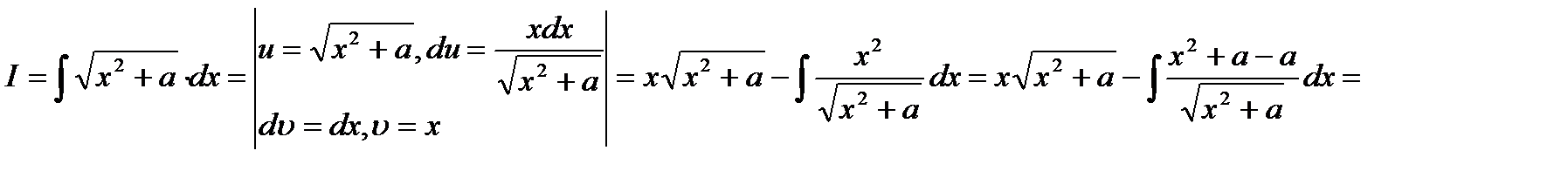
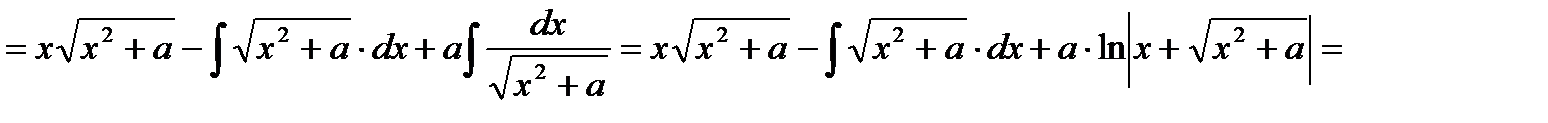
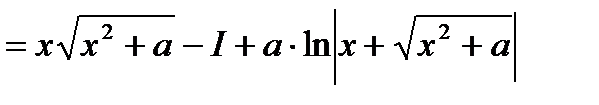 .
.
Получили равенство относительно искомого интеграла I, решив которое, получим:
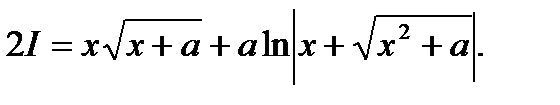
Откуда 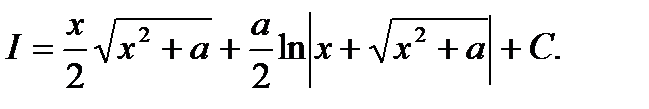
11)
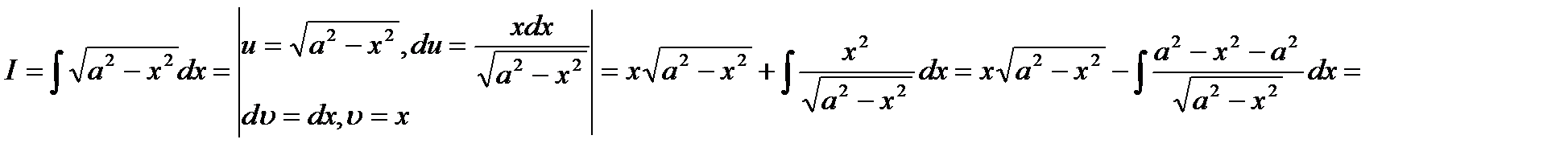
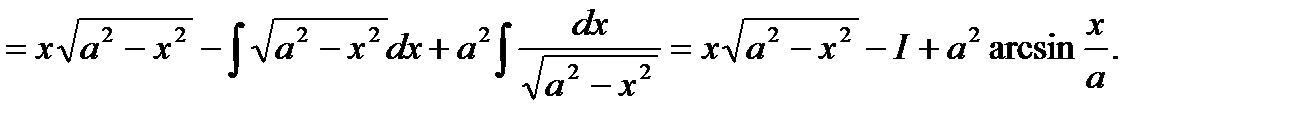
Т.о. 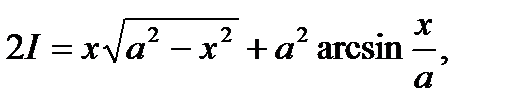
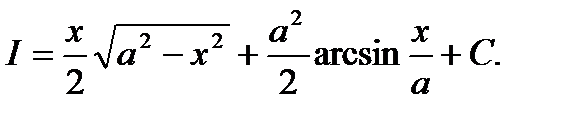
Иногда интегрирование по частям позволяет получить отношение между неопределенным интегралом, который содержит степень некоторой функции, и аналогичным интегралом, но с меньшим показателем степени этой же функции. Эти соотношения называются рекурентными формулами.
Пример 12. Найти рекурентную формулу для вычисления интеграла 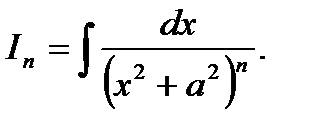

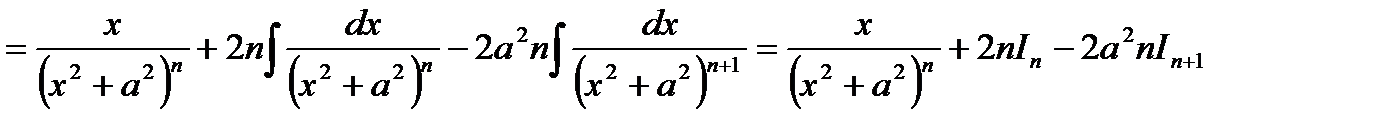
Откуда 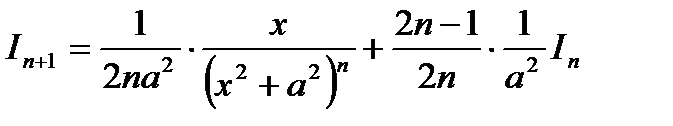
Эта формула позволяет вычислить интеграл 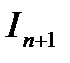 с помощью интеграла
с помощью интеграла 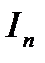 . Где
. Где 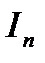 - интеграл с любым натуральным индексом и
- интеграл с любым натуральным индексом и 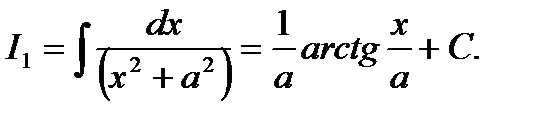
Рассмотрим интеграл вида 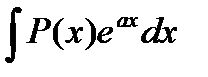 , где P(x) – многочлен.
, где P(x) – многочлен.
Пример 13.
стр.15 №34 (голубое пособие)
Для вычисления интегралов такого типа можно пользоваться методом неопределенных интегралов.
Пример 14. Найти метолом неопределенных коэффициентов. 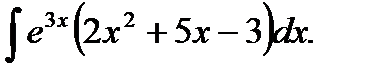
Будем полагать, что 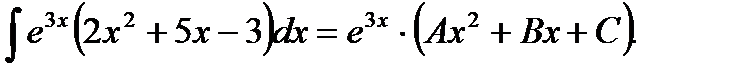
Продифференцируем это равенство и получим:
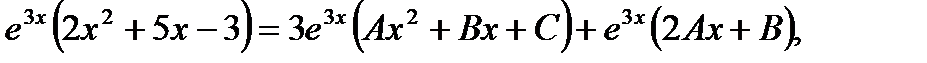 или
или
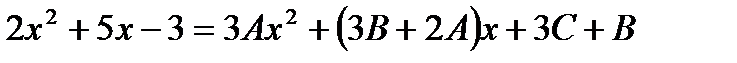 .
.
Прировняем коэффициенты при одинаковых степенях x, получим ситему для вычисления коэффициентов A,B,C:
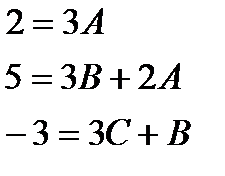
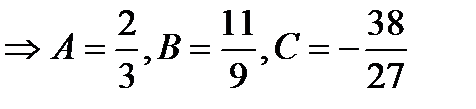 .
.
Т.о. получим: 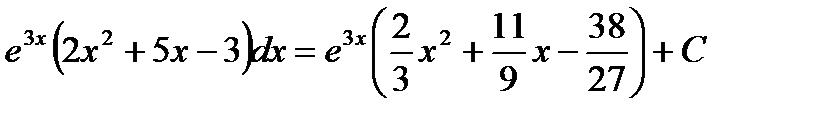 .
.
Методом неопределенных коэффициентов можно использовать для интегралов вида 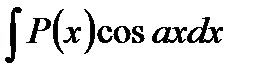 ,
,
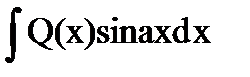 .
.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|