
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Экспоненциальное распределение
ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ
ВОЛГОГРАДСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
КАФЕДРА АВТОМАТИЗАЦИИ ПРОИЗВОДСТВЕННЫХ ПРОЦЕССОВ
Моделирование случайного процесса
Методические указания к лабораторной работе по дисциплине
“Моделирование систем”
РПК «Политехник»
Волгоград 2005
УДК 519:65.011.56
МОДЕЛИРОВАНИЕ СЛУЧАЙНОГО ПРОЦЕССА: Методические указания к лабораторной работе по дисциплине “Моделирование систем”/ Сост. А. Г. Кесоян, Л. А. Рабинович; Волгоград. гос. техн. ун-т. – Волгоград, 2005.– 12 с.
Приведено описание лабораторной работы “Моделирование случайного процесса”, в которой изучаются методы имитационного моделирования случайных величин, изменяющихся по заданным законам распределения.
Предназначены для студентов специальности 210200 всех форм обучения.
Ил. 5. Библиогр.: 8 назв.
Рецензент В. Г. Карабань
Печатается по решению редакционно-издательского совета Волгоградского государственного технического университета
| © | Волгоградский государственный технический университет, 2005 |
1. ЦЕЛЬ РАБОТЫ
1.1. Изучение моделирования случайных величин, распределяющихся по заданным законам.
1.2. Привитие навыков использования методов моделирования для формирования случайной выборки с заданным распределением случайных величин.
2. ОСНОВНЫЕ ПОЛОЖЕНИЯ
Имитационное моделирование является одним из наиболее эффективных средств исследования сложных систем и процессов. В настоящее время существенно расширилась область использования методов имитационного моделирования и включает технические, экономические, социальные и другие объекты исследования.
Имитационное моделирование широко используется на этапах проектирования и эксплуатации сложной системы: при проектировании – для осуществления параметрического и структурного синтеза, проведения многовариантного анализа; при эксплуатации – для прогнозирования эффекта от предполагаемых модернизаций состава и структуры сложной системы.
Имитационная модель отражает последовательность протекания различных процессов, и взаимодействие отдельных элементов во времени. При построении формализованной схемы процесса должно выполняться правило: событие, происходящее в момент времени ti может моделироваться только после того, как промоделированы все события, прошедшие в момент времени ti-1. Реализация этого правила может проводиться двумя способами, а именно:
1. Повременное моделирование с детерминированным шагом («принцип Dt»). Алгоритм одновременно просматривает все элементы системы через малые промежутки времени (шаг моделирования) и анализирует взаимодействия между элементами.
«Принцип Dt» является наиболее универсальным при построении моделирующих алгоритмов. Однако этот принцип неэкономичен, поскольку на каждом шаге необходимо просматривать состояние всех блоков системы. При увеличении интервала Dt появляется опасность пропуска отдельных событий в системе.
2. Событийный (позаявочный) способ или («принцип D z») при котором прослеживается прохождение каждой заявки (детали,) в порядке поступления их в систему. Алгоритм строится из условия, что текущее время в моделируемой системе изменяется дискретно, проходя последовательно через все события. Таким образом, состояние системы изменяется с момента времени наступления определенного события: поступления очередной заявки (детали) на обслуживание, окончания ее обработки и т. д. При событийном принципе интервалы времени, в которые просматривается состояние системы, изменяются с переменным шагом. Кроме того, просматриваются состояния не всех элементов системы, а только тех, в которых произошли события.
Такие алгоритмы экономичны, позволяют существенно уменьшить затраты машинного времени по сравнению с «принципом Dt», однако имеют сложную логическую структуру. Этот принцип может использоваться только в простых моделях в случае последовательных заявок.
В случаях, когда неприемлемо аналитическое моделирование, прибегают к универсальному методу имитационного (статистического) моделирования называемого методом Монте-Карло. Вместо того, чтобы описывать процесс с помощью аналитического аппарата (дифференциальных или алгебраических уравнений), производится «розыгрыш» случайного явления с помощью специально организованной процедуры (так называемый вероятностный эксперимент), включающей в себя случайность и дающей случайный результат. Вероятностный эксперимент – это совокупность действий или явлений, в которых сложное сочетание естественных причин ведет к случайному результату. Множество реализаций используется как статистический материал, который может быть обработан методами математической статистики. При имитационном моделировании метод Монте-Карло используется в следующих случаях:
1) при моделировании сложных комплексных операций, где присутствует много взаимодействующих случайных факторов;
2) при проверке применимости более простых, аналитических методов и выяснения условий их применимости;
3) в целях выработки поправок к аналитическим формулам типа «эмпирических формул» в технике.
Случайная величина – это функция, отображающая пространство элементарных событий в множество чисел. С каждым вероятностным экспериментом можно связать много разных случайных величин. Случайные величины измеряются и анализируются в терминах их статистических и вероятностных свойств, главным выразителем которых является функция распределения. Хотя возможных моделей распределения достаточно много, относительно небольшое их число особенно хорошо описывают действительность.
Основную роль в имитационном моделировании играют случайные величины, равномерно распределенные на интервале (0, 1); такие случайные числа обозначаются буквой R. Существует несколько способов получения значений R: таблицы случайных чисел, генераторы случайных чисел и метод псевдослучайных чисел.
Для воспроизведения распределения случайной величины по различным законам используются специальные модели имитации, которые основываются на преобразовании равномерно распределенных случайных чисел по соответствующим правилам.
1. Для получения случайных чисел с нормальным законом распределения используется сумма 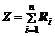 , где R1, R2, …, R n – независимые равномерно распределенные на интервале (0, 1) случайные величины. В соответствии с центральной предельной теоремой Z является асимптотически нормальной величиной со средним n/2 и дисперсией n/12. Пронормируем Z, то есть перейдем от нее к величине
, где R1, R2, …, R n – независимые равномерно распределенные на интервале (0, 1) случайные величины. В соответствии с центральной предельной теоремой Z является асимптотически нормальной величиной со средним n/2 и дисперсией n/12. Пронормируем Z, то есть перейдем от нее к величине 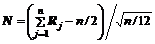 . Для практических расчетов можно принять n=12, тогда
. Для практических расчетов можно принять n=12, тогда
 . (1)
. (1)
Нормально распределенные случайные числа можно также получать, используя метод Бокса – Миллера из выражений:
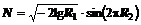 , (2)
, (2)
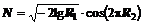 . (3)
. (3)
2. Для логарифмически нормального распределения случайные числа можно получить из выражений
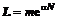 , (4)
, (4)
где m – медиана, s – среднее квадратическое отклонение.
3. Для распределения Релея случайные числа можно получить из выражений
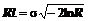 , (5)
, (5)
где s – среднее квадратическое отклонение.
4. Для экспоненциального распределения случайные числа можно получить из выражений
E=–b×lnR, (6)
где b – параметр масштаба.
3. ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ
Спланируем рациональное размещение данных в таблице в Excel.
Строку 1 отведем под заголовок таблицы. Выделим строку 2 от ячейки А2 до N2 и организуем рамку. В эти ячейки запишем наименования столбцов в соответствии с прилагаемой таблицей. Отформатируем данные по центру.
В столбце А, начиная с ячейки А4, запишем номера деталей от 1 до 100. Для этого в ячейки А3 и А4 запишем по 1, затем увеличим на единицу и т. д. до ячейки А103. В ячейку В3 запишем 2 и т. д. до 14 в ячейке N3.
Для моделирования случайных чисел, распределенных по нормальному закону, воспользуемся встроенной функцией СЛЧИС(), генерирующей равномерно распределенные на интервале 0...1 числа. Запишем в ячейки В4 и С4 функцию =СЛЧИС(). Содержимое этих ячеек скопируем до 103 строки включительно. Таким образом, произведено 100 экспериментов.
Для получения нормально распределенных случайных чисел N используем формулу (2) и запишем в ячейку D4 выражение =КОРЕНЬ(–2*LOG10(B4))*SIN(2*ПИ()*C4), скопируем его до ячейки D103.
Полученный массив необходимо рассортировать на 10 групп и подсчитать количество случайных чисел в каждой группе. Для этого определим минимальное и максимальное значение, а также ширину группы для чисел из столбца D. В ячейку D104 запишем =МИН(D4:D103), а в ячейку D105 – формулу =МАКС(D4:D103). В ячейку D106 запишем выражение =(D105-D104)/10.
Для сортировки массива случайных чисел на группы следует воспользоваться встроенными логическими функциями =ЕСЛИ(...), =И(...).
В ячейку Е4 запишем выражение =ЕСЛИ(И($D4>=((A$3-1)*$D$106+$D$104);$D4<=(A$3*$D$106+$D$104));1). Скопируем это выражение по строке 4 до ячейки N4. Если копирование выполнено верно, то после нажатия клавиши F9 в одной (и только в одной) из ячеек строки должна появиться единица. Затем скопируем ячейки Е4–N4 по строкам от Е5 до N103.
В строке 107 подсчитывается сумма случайных чисел, попавших в каждую группу, для этого в ячейку Е107 записывается формула =СУММ(E4:E103), которая копируется до ячейки N107.
| A | B | C | D | E | F | … | L | M | N | |
| Номер | R1 | R2 | N | Гр1 | Гр2 | … | Гр8 | Гр9 | Гр10 | |
| … | ||||||||||
| 0,3320 | 0,5417 | -0,2539 | ЛОЖЬ | ЛОЖЬ | … | ЛОЖЬ | ЛОЖЬ | ЛОЖЬ | ||
| 0,1799 | 0,5347 | -0,2646 | ЛОЖЬ | ЛОЖЬ | … | ЛОЖЬ | ЛОЖЬ | ЛОЖЬ | ||
| 0,9907 | 0,1103 | 0,0575 | ЛОЖЬ | ЛОЖЬ | … | ЛОЖЬ | ЛОЖЬ | ЛОЖЬ | ||
| 0,8283 | 0,5114 | -0,029 | ЛОЖЬ | ЛОЖЬ | … | ЛОЖЬ | ЛОЖЬ | ЛОЖЬ | ||
| 0,7118 | 0,6272 | -0,3894 | ЛОЖЬ | ЛОЖЬ | … | ЛОЖЬ | ЛОЖЬ | ЛОЖЬ | ||
| 0,9009 | 0,2521 | 0,301 | ЛОЖЬ | ЛОЖЬ | … | ЛОЖЬ | ЛОЖЬ | ЛОЖЬ | ||
| 0,7468 | 0,1608 | 0,4266 | ЛОЖЬ | ЛОЖЬ | … | ЛОЖЬ | ЛОЖЬ | ЛОЖЬ | ||
| ... | ... | ... | ... | ... | ... | ... | … | ... | ... | ... |
| 0,3779 | 0,2180 | 0,9008 | ЛОЖЬ | ЛОЖЬ | … | ЛОЖЬ | ЛОЖЬ | |||
| 0,8243 | 0,9084 | -0,2228 | ЛОЖЬ | ЛОЖЬ | … | ЛОЖЬ | ЛОЖЬ | ЛОЖЬ | ||
| 0,2800 | 0,7086 | -1,0162 | ЛОЖЬ | ЛОЖЬ | … | ЛОЖЬ | ЛОЖЬ | ЛОЖЬ | ||
| 0,9583 | 0,2093 | 0,1859 | ЛОЖЬ | ЛОЖЬ | … | ЛОЖЬ | ЛОЖЬ | ЛОЖЬ | ||
| 0,9549 | 0,5920 | -0,1094 | ЛОЖЬ | ЛОЖЬ | … | ЛОЖЬ | ЛОЖЬ | ЛОЖЬ | ||
| 0,6342 | 0,8234 | -0,5631 | ЛОЖЬ | ЛОЖЬ | … | ЛОЖЬ | ЛОЖЬ | ЛОЖЬ | ||
| 0,5323 | 0,1546 | 0,6112 | ЛОЖЬ | ЛОЖЬ | … | ЛОЖЬ | ЛОЖЬ | |||
| 0,2973 | 0,7672 | -1,0203 | ЛОЖЬ | ЛОЖЬ | … | ЛОЖЬ | ЛОЖЬ | ЛОЖЬ | ||
| 0,4275 | 0,6405 | -0,664 | ЛОЖЬ | ЛОЖЬ | … | ЛОЖЬ | ЛОЖЬ | ЛОЖЬ | ||
| 0,3695 | 0,7330 | -0,9246 | ЛОЖЬ | ЛОЖЬ | … | ЛОЖЬ | ЛОЖЬ | ЛОЖЬ | ||
| 0,6338 | 0,4921 | 0,0311 | ЛОЖЬ | ЛОЖЬ | … | ЛОЖЬ | ЛОЖЬ | ЛОЖЬ | ||
| 0,261 | 0,4613 | 0,2597 | ЛОЖЬ | ЛОЖЬ | … | ЛОЖЬ | ЛОЖЬ | ЛОЖЬ | ||
| 0,0494 | 0,2175 | 1,5824 | ЛОЖЬ | ЛОЖЬ | … | ЛОЖЬ | ЛОЖЬ | |||
| 0,9028 | 0,7948 | -0,2862 | ЛОЖЬ | ЛОЖЬ | … | ЛОЖЬ | ЛОЖЬ | ЛОЖЬ | ||
| Мин | -1,9534 | … | ||||||||
| Макс | 1,58242 | … | ||||||||
| Инт | 0,35358 | … | ||||||||
| Итого | … | |||||||||
Используя Мастер диаграмм построить гистограммы нормально распределенных случайных чисел по рассортированным группам в ячейках E107–N107. Нажимая клавишу F9, наблюдать изменение графиков.
Зарисовать два графика нормального распределения в соответствии с примером, приведенным на рис. 1.
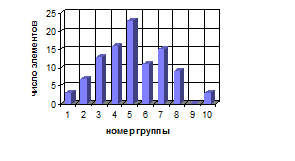
Рис. 1. Нормальное распределение случайных величин
3.1 Логарифмически нормальное распределение
Для получения случайных величин, имеющих логарифмически нормальное распределение, воспользуемся формулой (4). Примем m=1, s=1 и используем созданную таблицу. Так как в Excel при производимых изменениях происходит смена адресов ячеек, то полученный массив будет автоматически рассортирован на 10 групп. Вставим столбец Е, запишем в ячейку Е2 название переменной L, исправим возрастающие числа в строке 3. Запишем в ячейку Е4 выражение =exp(D4) и скопируем его до ячейки Е103. Скопируем выражения из ячеек D104-D106 в Е104-Е106. Исправим содержимое ячейки F4, записав в нее выражение =ЕСЛИ(И ($E4>=((A$3-1)*$E$106+$E$104);$E4<=(A$3*$E$106+$E$104));1) и скопируем его до ячейки O103. Перенесем содержимое ячеек С104-С107 в ячейки D104-D107. Нажимая клавишу F9, наблюдать изменение графиков.
Зарисовать два графика логарифмически нормального распределения в соответствии с примером, приведенным на рис. 2.

Рис. 2. Логарифмически нормальное распределение случайных величин
3.2 Распределение Релея
Для получения случайных величин, распределенных по закону Релея, используем имеющуюся таблицу и воспользуемся формулой (5). Примем s=1. Перенесем содержимое ячеек D104-D107 в ячейки В104-В107. Запишем в ячейку E2 название переменной Rl, а в ячейку E4 выражение =КОРЕНЬ(-2*LN(B4)) и скопируем его до ячейки E103. Удалим столбцы С и D. В строке 3 восстановим возрастание номеров от 1 до 13 и проверим выражение в ячейке D4, которое должно иметь вид: =ЕСЛИ(И ($C4>=((A$3-1)*$C$106+$C$104);$C4<=(A$3*$C$106+$C$104));1). При необходимости внести изменения и скопировать его до ячейки М103. Проверить и внести исправления в строку 107. Нажимая клавишу F9, наблюдать изменение графиков.
Зарисовать два графика распределения Релея в соответствии с примером, приведенным на рис. 3.
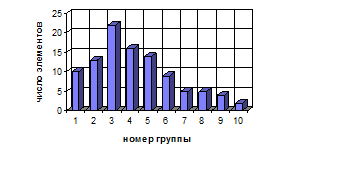
Рис. 3. Распределение случайных величин по закону Релея
3.3 Экспоненциальное распределение
Для получения случайных величин, распределенных по экспоненциальному закону, используем имеющуюся таблицу и воспользуемся формулой (6). Примем b=1. Запишем в ячейку С2 название переменной Е, а в ячейку С4 выражение =-LN(B4) и скопируем его до ячейки С103. Если в таблице произошли изменения адресов ссылок, то в строке 3 восстановить возрастание номеров от 1 до 13, проверить выражение в ячейке D4, которое должно иметь вид: =ЕСЛИ(И($C4>=((A$3-1)*$C$106+$C$104);$C4<=(A$3*$C$106+$C$104));1), при необходимости внести изменения и скопировать его до ячейки М103. Нажимая клавишу F9, наблюдать изменение графиков.
Зарисовать два графика экспоненциального распределения в соответствии с примером, приведенным на рис. 4.

Рис. 4. Экспоненциальное распределение случайных величин
3.4 Равновероятное распределение
Для получения случайных величин, имеющих равновероятное распределение, используем имеющуюся таблицу. Перенесем содержимое ячеек В104-В107 в ячейки А104-А107 и скопируем выражения из ячеек С104-С106 в ячейки В104-В106. Удалим столбец С, в строке 3 восстановим возрастание номеров от 1 до 12 и исправим содержимое ячейки С4, записав в нее выражение =ЕСЛИ(И($B4>=((A$3-1)*$B$106+$B$104);$B4<=(A$3*$B$106+$B$104));1) и скопируем его до ячейки L103. Нажимая клавишу F9, наблюдать изменение графиков.
Зарисовать два графика равновероятного распределения в соответствии с примером, приведенным на рис. 5.
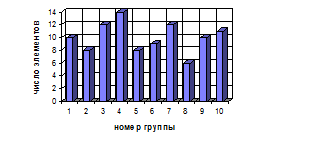
Рис. 5. Равновероятное распределение случайных величин
4. СОДЕРЖАНИЕ ОТЧЕТА
1. Цель работы.
2. Формулы генерирования случайных чисел для заданного закона распределения.
3. Гистограммы распределения по группам случайных величин.
4. Выводы и заключение по выполненной работе.
5. КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Основные понятия моделирования.
2. Требования, предъявляемые к моделям.
3. Классификация технических систем.
4. Классификация моделей.
5. Метод имитационного моделирования.
6. Моделирование случайных чисел с заданным законом распределения случайных величин.
7. Принципы построения имитационных моделирующих алгоритмов.
СПИСОК РЕКОМЕНДУЕМОЙ ЛИТЕРАТУРЫ
1. Соболь И. М. Метод Монте-Карло.–М.: Наука, 1978.–64 с.
2. Лукьянов В. С. Решение задач в машиностроении методами имитационного моделирования. Учебное пособие. Волгоград. Изд. ВолгПИ, 1989, 26 с.
3. Бусленко Н. П. Моделирование сложных систем.–М.: Наука, 1978.–310 с.
4. Советов Б. Я., Яковлев С. А. Моделирование систем.–М.: Наука, 1998.–146 с.
5. Основы моделирования сложных систем/ Под ред. Л. И. Дыхненко.–Киев: Технiка, 1981.–359 с.
6. Основы моделирования сложных систем/ Под ред. В. В. Налимова.–М.: Высш. шк., 1981.–358 с.
7. Таха Х. Введение в исследование операций: В 2-х книгах. Кн. 2.–М.: Мир, 1985.–496 с.
8. Прицкер А. Введение в имитационное моделирование и язык СЛАМ II.–М.: Мир, 1987.–646 с.
Составители Аркадий Георгиевич Кесоян
Леонид Абрамович Рабинович
МОДЕЛИРОВАНИЕ СЛУЧАЙНОГО ПРОЦЕССА
Методические указания к лабораторной работе
по дисциплине «Моделирование систем»
Темплан 2005 г., поз. № 52
Подписано в печать 10.02.2005. Формат 60 х84 1/16.
Бумага газетная. Печать офсетная. Усл. печ. л. 0,7
Тираж 100 экз. Заказ. . Бесплатно.
Волгоградский государственный технический университет.
400131 Волгоград, просп. им. Ленина, 28
РПК “Политехник” Волгоградского государственного технического университета
400131 Волгоград, ул. Советская, 35
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|