
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Итерационные методы для решения систем линейных алгебраических уравнений
Итерационные методы для решения систем линейных алгебраических уравнений


Метод Зейделя
Постановка задачи
Возьмём систему: 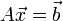 , где
, где 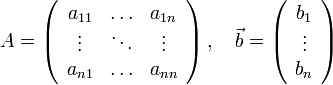
Или 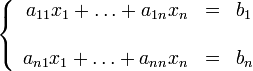
И покажем, как её можно решить с использованием метода Гаусса-Зейделя.
Метод
Чтобы пояснить суть метода, перепишем задачу в виде:
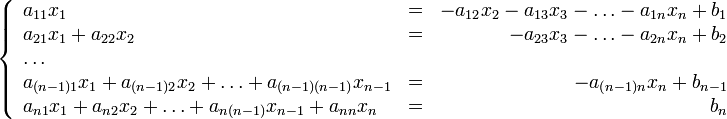
Здесь в 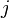 -м уравнении мы перенесли в правую часть все члены, содержащие
-м уравнении мы перенесли в правую часть все члены, содержащие 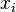 , для
, для 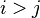 . Эта запись может быть представлена:
. Эта запись может быть представлена:
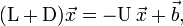
где в принятых обозначениях 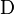 означает матрицу, у которой на главной диагонали стоят соответствующие элементы матрицы
означает матрицу, у которой на главной диагонали стоят соответствующие элементы матрицы 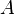 , а все остальные нули; тогда как матрицы
, а все остальные нули; тогда как матрицы 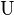 и
и 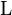 содержат верхнюю и нижнюю треугольные части
содержат верхнюю и нижнюю треугольные части 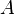 , на главной диагонали которых нули.
, на главной диагонали которых нули.
Итерационный процесс в методе Гаусса-Зейделя строится по формуле 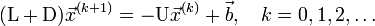 после выбора соответствующего начального приближения
после выбора соответствующего начального приближения 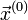 .
.
Метод Гаусса-Зейделя можно рассматривать как модификацию метода Якоби. Основная идея модификации состоит в том, что новые значения 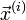 используются здесь сразу же по мере получения, в то время как в методе Якоби они не используются до следующей итерации:
используются здесь сразу же по мере получения, в то время как в методе Якоби они не используются до следующей итерации:
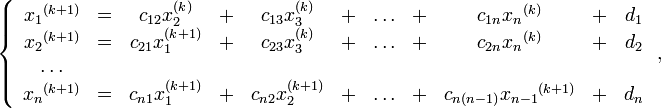
где 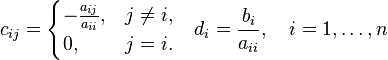
Таким образом, i-тая компонента 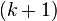 -го приближения вычисляется по формуле:
-го приближения вычисляется по формуле:
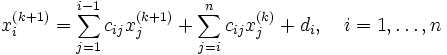
Например, при 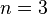
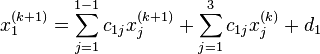 , то есть
, то есть 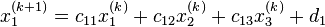
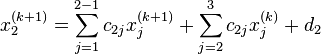 , то есть
, то есть 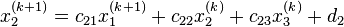
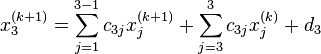 , то есть
, то есть 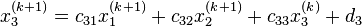
Метод Релаксации

Выбирается начальное приближение 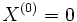 . На каждом шаге необходимо обратить в ноль максимальную невязку:
. На каждом шаге необходимо обратить в ноль максимальную невязку: 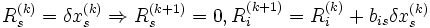 .
.
Условие остановки: 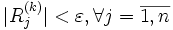 .
.
Ответ находится по формуле: 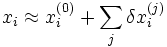 .
.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|