
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Способ подстановки (замены переменных).
Способ подстановки (замены переменных).
Теорема: Если требуется найти интеграл 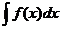 , но сложно отыскатьпервообразную, то с помощью замены x = j(t) и dx = j¢(t)dt получается:
, но сложно отыскатьпервообразную, то с помощью замены x = j(t) и dx = j¢(t)dt получается:
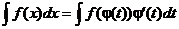
Доказательство: Продифференцируем предлагаемое равенство:
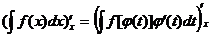
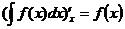
правая часть данного равенства есть сложная функция от «х»; t-промежуточная переменная.
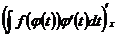 =
= 
Если интеграл в правой части окажется табличным, то задача будет решена.
Пример 1. Найти неопределенный интеграл 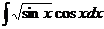 .
.
Сделаем замену t = sinx, dt = cosxdt.
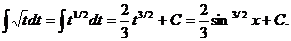
Пример 2. 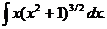
Замена 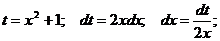 Получаем:
Получаем:
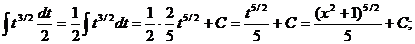
Пример 3.
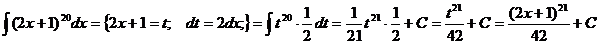
Пример 4.
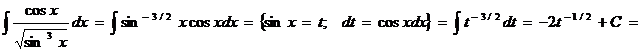
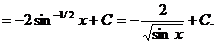
Интегрирование по частям.
Способ основан на известной формуле производной произведения:
(uv)¢ = u¢v + v¢u
где u и v– некоторые функции от х.
В дифференциальной форме: d(uv) = udv + vdu
Проинтегрировав, получаем: 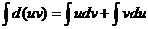 , а в соответствии с приведенными выше свойствами неопределенного интеграла:
, а в соответствии с приведенными выше свойствами неопределенного интеграла:
 или
или 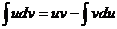 ;
;
Получили формулу интегрирования по частям, которая позволяет находить интегралы многих элементарных функций.
Полученная формула называется формулой интегрирования по частям. По частям берутся интегралы вида:
1) 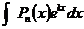

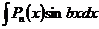
В этих интегралах в качестве u всегда берется 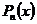
Пример.
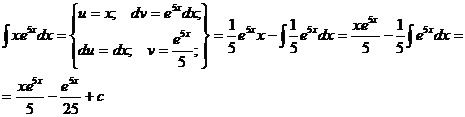
2) 
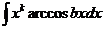
3) 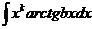
Здесь за uвсегда принимают обратную тригонометрическую функцию.
4) 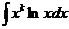
За u принимают lnx.
Пример:
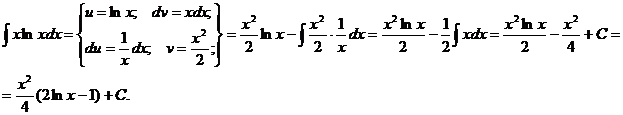
По частям берутся также интегралы вида:
 и
и 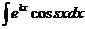
Двукратным применением формулы интегрирования по частям эти интегралы приводятся сами к себе (т.н. интегралы возврата). Получается алгебраическое уравнение относительно искомого интеграла.
Пример: 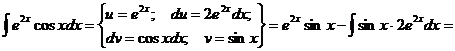
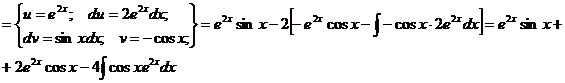
Видно, что в результате повторного применения интегрирования по частям функцию не удалось упростить к табличному виду. Однако последний полученный интеграл ничем не отличается от исходного. Поэтому перенесем его в левую часть равенства.
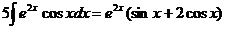
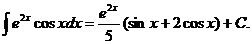
Таким образом, интеграл найден вообще без применения таблиц интегралов.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|