
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Обычный алгоритм Монте-Карло интегрирования
Лекция. Имитационное моделирование.
Метод Монте-Карло (методы Монте-Карло, ММК) — общее название группы численных методов, основанных на получении большого числа реализаций стохастического (случайного) процесса, который формируется таким образом, чтобы его вероятностные характеристики совпадали с аналогичными величинами решаемой задачи. Используется для решения задач в областях физики, математики, экономики, оптимизации, теории управления и др.
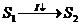
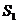 — первоначальное состояние системы (система 1);
— первоначальное состояние системы (система 1);
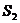 — новое состояние системы (система 2);
— новое состояние системы (система 2);
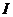 — факторы, внутренние и внешние, влияющие на систему 1, под действием которых она переходит в систему 2.
— факторы, внутренние и внешние, влияющие на систему 1, под действием которых она переходит в систему 2.
Мы не можем узнать, какие факторы будут воздействовать на систему, но можем предложить вероятности исхода. Необходимо найти закон распространения вероятностей.
Для изучения поведения заданной статистики при проведении многократных повторных выборок, используется метод Монте-Карло. При проведении анализа этим компьютер использует процедуру генерации псевдослучайных чисел для имитации данных из изучаемой генеральной совокупности. Процедура анализа состоит в том, что необходимо построить выборки из генеральной совокупности в соответствии с указаниями пользователя.
Обычный алгоритм Монте-Карло интегрирования
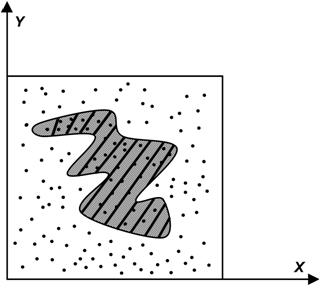
Предположим, необходимо взять интеграл от некоторой функции. Воспользуемся неформальным геометрическим описанием интеграла и будем понимать его как площадь под графиком этой функции.
Для определения площади фигуры можно использовать следующий стохастический алгоритм:
- ограничим функцию прямоугольником (n-мерным параллелепипедом в случае многих измерений), площадь которого
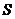 можно легко вычислить;
можно легко вычислить; - «набросаем» в этот прямоугольник (параллелепипед) некоторое количество точек (
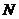 штук), координаты которых будем выбирать случайным образом;
штук), координаты которых будем выбирать случайным образом; - определим число точек (
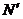 штук), которые попадут под график функции;
штук), которые попадут под график функции; - площадь области, ограниченной функцией и осями координат, S даётся следующим выражением:
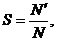 где
где
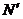 — количество точек, попавших в фигуру;
— количество точек, попавших в фигуру;
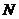 — общее количество точек.
— общее количество точек.
По методу Монте-Карло, чем больше точек, тем точнее будет вычислена площадь фигуры 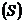 , т.е., чем больше «выбросов», тем более точную оценку математического ожидания мы получим.
, т.е., чем больше «выбросов», тем более точную оценку математического ожидания мы получим.
Пример.
| Объем спроса | Частота | Вероятность 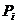
| 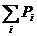
| Интервалы случайных чисел |
| 0,05 | 0,05 | 01-05 | ||
| 0,1 | 0,15 | 06-15 | ||
| 0,2 | 0,35 | 16-34 | ||
| 0,3 | 0,65 | 36-65 | ||
| 0,2 | 0,85 | 66-85 | ||
| 0,1 | 0,95 | 86-95 | ||
| 0,05 | 96-00 |
Накопленная вероятность описывается интегральной функцией Лапласа.
При попадании числа в определенный интервал выбирается определенный объем спроса с определенной вероятностью.
Для решения задачи смотрим в таблицу случайных чисел, т.к. нам необходимо определить математическое ожидание 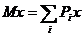 . При равновероятных событиях математическое ожидание определяется следующей формулой:
. При равновероятных событиях математическое ожидание определяется следующей формулой: 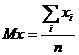 .
.
| Случайное число | Объем спроса |
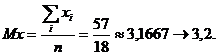
Необходимо определить точность расчетов. Предположим, что предположим, что 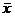 — характеристика, которая должна быть определена (в нашем случае математическое ожидание), а
— характеристика, которая должна быть определена (в нашем случае математическое ожидание), а 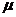 — ее значение, уточняемое по мере накопления данных, остающееся случайным вследствие ограниченности числа
— ее значение, уточняемое по мере накопления данных, остающееся случайным вследствие ограниченности числа  проведенных наблюдений. В этих условиях можно говорить о вероятности
проведенных наблюдений. В этих условиях можно говорить о вероятности 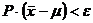 по отношению к интересующей нас характеристике
по отношению к интересующей нас характеристике 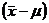 представляет собой погрешность в оценке
представляет собой погрешность в оценке 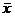 , а
, а 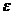 — некоторый допустимый ее предел.
— некоторый допустимый ее предел.
В нашем примере 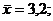
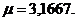
Пусть 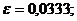
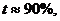
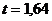 (табличная величина);
(табличная величина); 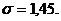
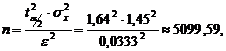
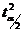 — критерий Стьюдента, количество стандартных ошибок при заданном уровне значимости
— критерий Стьюдента, количество стандартных ошибок при заданном уровне значимости 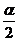 ;
;
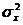 — дисперсия случайной величины
— дисперсия случайной величины 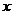 ;
;
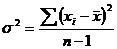 — несмещенная оценка.
— несмещенная оценка.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|