
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
ИНТЕГРИРОВАНИЕ ДРОБНО-РАЦИОНАЛЬНЫХ ФУНКЦИЙ
ИНТЕГРИРОВАНИЕ ДРОБНО-РАЦИОНАЛЬНЫХ ФУНКЦИЙ
ПЛАН ЛЕКЦИИ
I. Определение дробно-рациональной функции. Простейшие дроби
II. Разложение правильной дроби на простейшие. Метод неопределенных коэффициентов
III. Интегрирование простейших дробей
IV. Правила интегрирования дробно-рациональных функций
V. Метод Остроградского
I. Определение дробно-рациональной функции. Простейшие дроби.Дробно-рациональной функцией называется функция вида
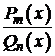 , (1)
, (1)
где 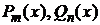 – многочлены степеней m и n соответственно. В дальнейшем считаем, что коэффициенты этих многочленов действительные числа, и
– многочлены степеней m и n соответственно. В дальнейшем считаем, что коэффициенты этих многочленов действительные числа, и 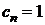 .
.
Если степень числителя меньше степени знаменателя, т.е. 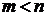 , то дробь (1) называют правильной. Если степень числителя больше или равна степени знаменателя, т.е.
, то дробь (1) называют правильной. Если степень числителя больше или равна степени знаменателя, т.е. 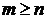 , то дробь называют неправильной. В последнем случае, выполняя деление числителя на знаменатель, дробь (1) можно представить как сумму многочлена и правильной рациональной дроби.
, то дробь называют неправильной. В последнем случае, выполняя деление числителя на знаменатель, дробь (1) можно представить как сумму многочлена и правильной рациональной дроби.
Простейшими дробями называют дроби следующих четырех типов:
1. 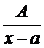 , 2.
, 2. 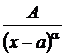 , 3.
, 3. 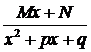 , 4.
, 4. 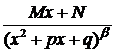 ,
,
где  .
.
II. Разложение правильной дроби на простейшие. Метод неопределенных коэффициентов. Всякую правильную рациональную дробь можно представить как алгебраическую сумму простейших дробей. Ранее было показано, что всякий многочлен с действительными коэффициентами может быть разложен на линейные и квадратичные множители. Представим в виде такого разложения знаменатель дроби (1):
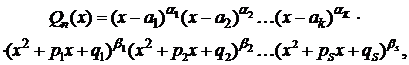 (2)
(2)
где 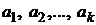 - действительные корни многочлена
- действительные корни многочлена 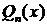 кратностей
кратностей 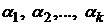 соответственно, а квадратные трехчлены
соответственно, а квадратные трехчлены 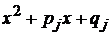 соответствуют комплексно сопряженным корням этого многочлена с кратностями
соответствуют комплексно сопряженным корням этого многочлена с кратностями 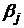 .
.
Тогда дробь (1) можно представить как сумму следующих простейших дробей:
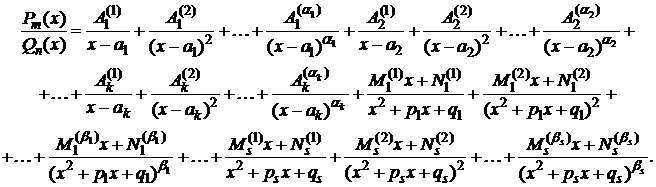
Последнее соотношение представляет собой тождество при определенном выборе постоянных 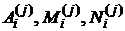 . Константы
. Константы 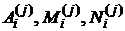 могут быть найдены методом неопределенных коэффициентов. Этот метод состоит в том, что дроби в правой части приводятся к общему знаменателю, который в силу (2) равен
могут быть найдены методом неопределенных коэффициентов. Этот метод состоит в том, что дроби в правой части приводятся к общему знаменателю, который в силу (2) равен 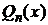 . Тогда в левой и правой частях получим две дроби с равными знаменателями и, следовательно, с равными числителями. Приравнивая
. Тогда в левой и правой частях получим две дроби с равными знаменателями и, следовательно, с равными числителями. Приравнивая 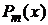 к многочлену с неопределенными коэффициентами
к многочлену с неопределенными коэффициентами 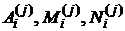 , получим систему уравнений относительно
, получим систему уравнений относительно 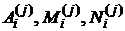 .
.
Пример 1. Разложить на простейшие дробь 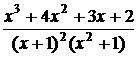 .
.
Решение: 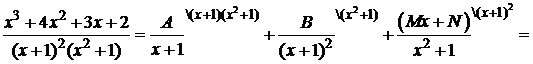
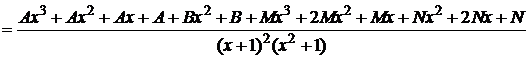
Приравняем числители:

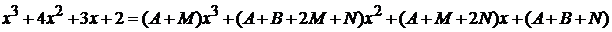 .
.
Два многочлена равны, если равны коэффициенты при одинаковых степенях x:
 x3: 1=A+M 2=2NN=1
x3: 1=A+M 2=2NN=1
x2: 4=A+B+2M+N 2=2M M=1
=>  =>
=>
x : 3=A+M+2NA=1-MA=0
x0: 2=A+B+NB=2-A-NB=1
Тогда:
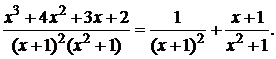
III. Интегрирование простейших дробей. Рассмотрим интегралы от простейших дробей четырех типов:
1) 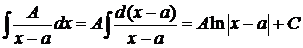 ;
;
2) 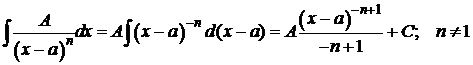 ;
;
3) 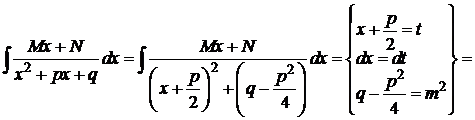
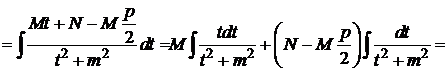
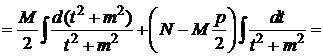
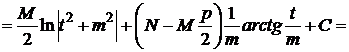
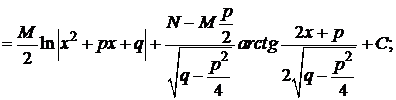
4) 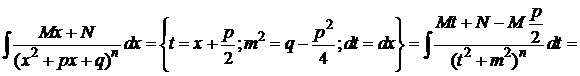
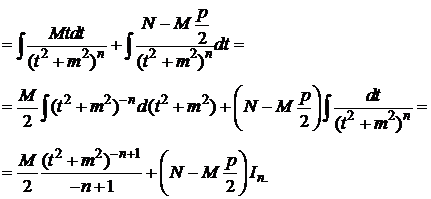
Найдем
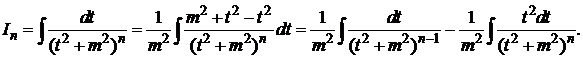
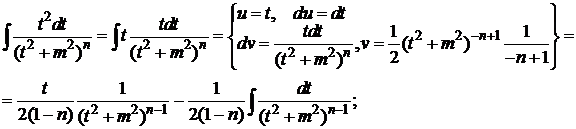
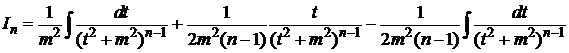
или
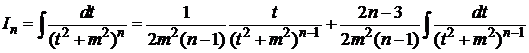 .
.
Получим рекуррентную формулу
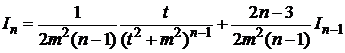 , (3)
, (3)
позволяющую интеграл 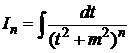 свести к интегралу
свести к интегралу 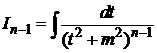 .
.
Применяя соотношение (3) n раз, интеграл 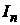 можно свести к табличному интегралу
можно свести к табличному интегралу
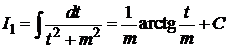 .
.
Пример 2. Найти неопределенный интеграл 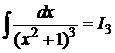 .
.
Решение. Воспользуемся формулой (3) для 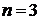 :
:
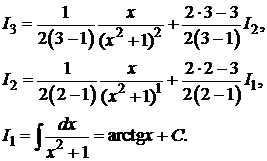
Тогда:
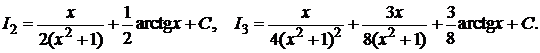
IV. Правила интегрирования дробно-рациональных функций. Сформулируем общие правила интегрирования таких функций:
1) определяем, является ли рассматриваемая дробь правильной или неправильной; в случае, когда дробь неправильная, представляем ее в виде суммы многочлена и правильной рациональной дроби;
2) правильную рациональную дробь представляем как сумму простейших дробей с неизвестными коэффициентами;
3) коэффициенты разложения находим по методу неопределенных коэффициентов;
4) интеграл от исходной дроби в общем случае представляется как сумма интегралов от многочлена (если 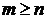 ) и от простейших дробей.
) и от простейших дробей.
Пример 3. Найти неопределенный интеграл 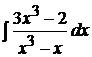 .
.
Решение.
1. Интегрируемая дробь является неправильной, поэтому разделим числитель на знаменатель и получим 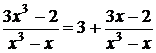 . (4)
. (4)
2. Разложим правильную дробь 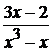 на простейшие:
на простейшие:
 ;
;
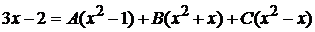 ;
;
 x2: 0=A+B+CA=2 A=2
x2: 0=A+B+CA=2 A=2
x : 3=B-C => 2B=1 => 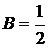
x0: -2=-A C=B-3 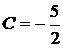
Получим 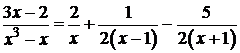 . (5)
. (5)
3. С учетом (4) и (5) найдем интеграл
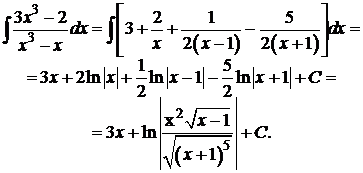
V. Метод Остроградского.Русским математиком Михаилом Васильевичем Остроградским предложен метод интегрирования рациональных дробей, который значительно упрощает задачу в том случае, когда знаменатель имеет кратные корни. В соответствии с этим методом интеграл от дробно-рациональной функции 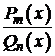 представим в виде
представим в виде
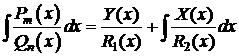 , (6)
, (6)
где 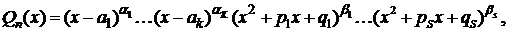
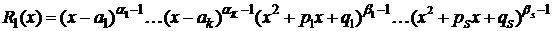 ,
,
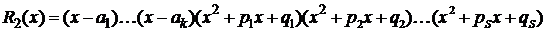 .
.
Многочлены 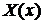 и
и 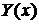 являются многочленами с неопределенными коэффициентами, степень которых на единицу меньше степеней многочленов
являются многочленами с неопределенными коэффициентами, степень которых на единицу меньше степеней многочленов 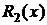 и
и 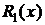 соответственно. Коэффициенты этих многочленов можно найти, продифференцировав равенство (6), методом неопределенных коэффициентов.
соответственно. Коэффициенты этих многочленов можно найти, продифференцировав равенство (6), методом неопределенных коэффициентов.
Пример 4. Найти интеграл 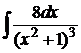 методом Остроградского.
методом Остроградского.
Решение. В соответствии с формулой (6) представим интеграл как сумму
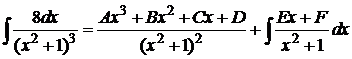 .
.
Найдем производные от левой и правой частей записанного равенства:
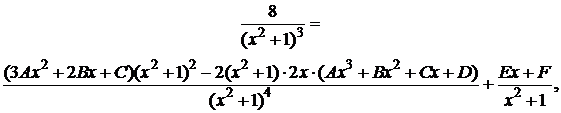
или после преобразований
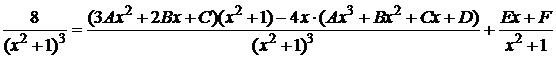 ,
,
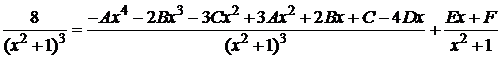 .
.
Приведем к общему знаменателю дроби в правой части равенства и приравняем числители
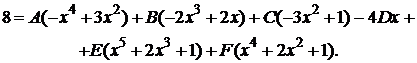
Приравнивая коэффициенты при одинаковых степенях х, получим систему для определения коэффициентов 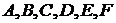 :
:
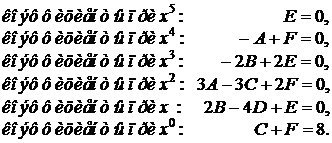
Решая эту систему, находим 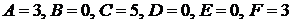 . Искомый интеграл равен
. Искомый интеграл равен
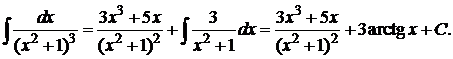
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|