Второй этап всероссийской олимпиады школьников по математике

Второй этап всероссийской олимпиады школьников по математике

2015-2016 учебный год

11 класс (задания)

1. Можно ли представить число 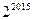в виде суммы некоторого числа последовательных натуральных чисел?

2. Решите уравнение:

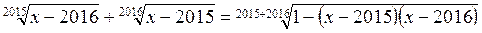3. Докажите, что в тетраэдре плоскость, делящая пополам любой из его двугранных углов, делит противолежащее ребро на отрезки, пропорциональные площадям граней, образующих данный двугранный угол.

4. Докажите, что 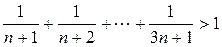для любого натурального .

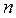5. Пять мальчишек во дворе играли в пиратов. Четверым из них было девять лет, а одному восемь. Они нашли клад в 2015 монет по 10 рублей и стали его делить следующим образом: старший из пиратов предлагает свой вариант дележа клада, а затем все голосуют. Если сумма возрастов ребят проголосовавших за предложенный вариант дележа не меньше суммы возрастов ребят, проголосовавших против, то предложенный вариант принимается. В противном случае, пират, предложивший вариант прогоняется со двора, а оставшиеся повторяют процедуру дележа. Будем считать, что каждый из мальчишек хочет получить как можно больше монет и остаться во дворе. Каким образом будет разделен клад между пиратами?