
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Вариант № 1. Вариант № 2. Вариант № 3. Вариант № 4. Вариант № 5. Вариант № 6. Вариант № 7. Вариант № 8. Вариант № 9. Вариант № 10 . Вариант № 11. Вариант № 12. Вариант № 13. Вариант № 14. Вариант № 15. Вариант № 16. Вариант № 17. Вариант № 18. Вариант № 1
ГБПОУ Региональный железнодорожный техникум
Расчетно-графическая работа №3
««Вычисление и применение производных и пределов»
по предмету
«Прикладная математика»
для групп 2-го курса специальностей
08.02.10 «Строительство железных дорог, путь и путевое хозяйство»
23.02.06 «Техническая эксплуатация подвижного состава железных дорог»
Составлена
преподавателем
Орловой С.И
Брянск – 2019г.
1. Вычислить пределы не используя правило Лопиталя (общая часть задания) Найдите пределы функции 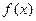 при
при  , если:
, если:
Индивидуальные варианты
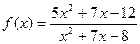 при при  , если , если 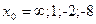
| 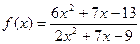 при при  , если , если 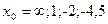
| ||
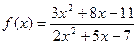 при при  , если , если 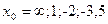
| 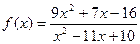 при при  , если , если 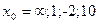
| ||
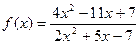 при при  , если , если 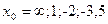
| 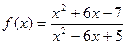 при при  , если , если 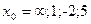
| ||
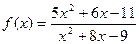 при при  , если , если 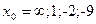
| 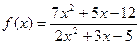 при при  , если , если 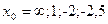
| ||
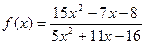 при при  , если , если 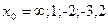
| 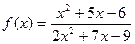 при при  , если , если 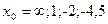
| ||
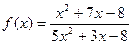 при при  , если , если 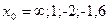
| 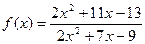 при при  , если , если 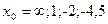
| ||
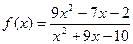 при при  , если , если 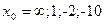
| 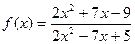 при при  , если , если 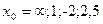
| ||
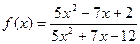 при при  , если , если 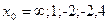
| 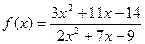 при при  , если , если 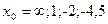
| ||
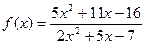 при при  , если , если 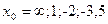
| 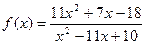 при при  , если , если 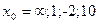
| ||
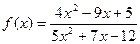 при при  , если , если 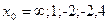
| 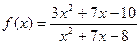 при при  , если , если 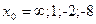
| ||
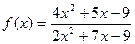 при при  , если , если 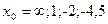
| 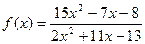 при при  , если , если 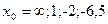
| ||
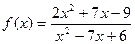 при при  , если , если 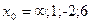
| 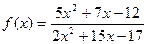 при при  , если , если 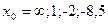
| ||
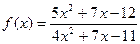 при при  , если , если 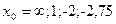
| 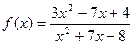 при при  , если , если 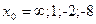
| ||
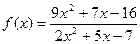 при при  , если , если 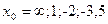
| 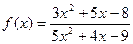 при при  , если , если 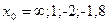
| ||
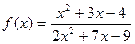 при при  , если , если 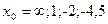
| 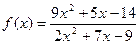 при при  , если , если 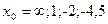
|
2. Вычислить пределы функций, не применяя правило Лопиталя:
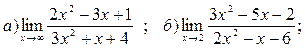 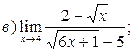
| а) 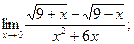 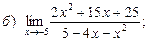 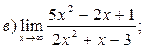
| ||
а) 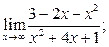 б) б) 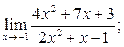 в)
в) 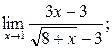
| а) 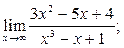 б) б) 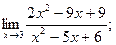 в)
в) 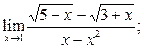
| ||
а) 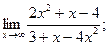 б) б) 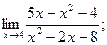 в)
в) 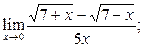
| а) 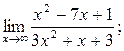 б) б) 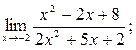 в)
в) 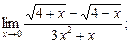
| ||
а) 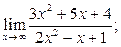 б) б) 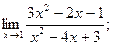 в)
в) 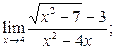
| а) 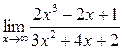 ;б) ;б) 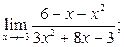 в)
в) 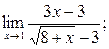
| ||
а) 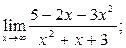 б) б) 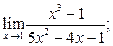 б)
б) 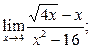
| а) 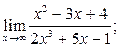 б) б) 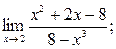 б)
б) 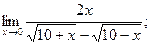
| ||
а) 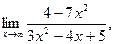 б) б) 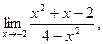 в) в) 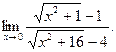
| а) 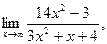 б) б) 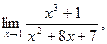 в) в) 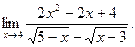
| ||
а) 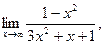 б) б) 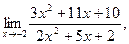 в) в) 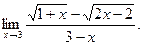
| а) 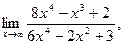 б) б) 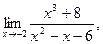 в) в) 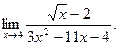
| ||
а) 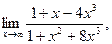 б) б) 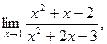 в) в) 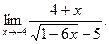
| а) 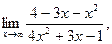 б) б) 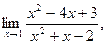 в) в) 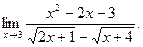
| ||
а) 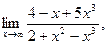 б) б) 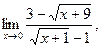 в) в) 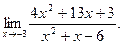
| а) 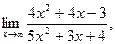 б) б) 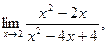 в) в) 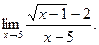
| ||
а) 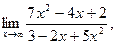 б) б) 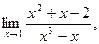 в) в) 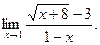
| а) 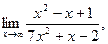 б) б) 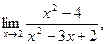 в) в) 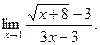
| ||
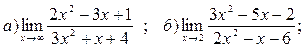 в) в) 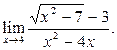
| а) 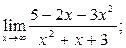 б) б) 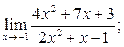 в)
в) 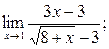
| ||
а) 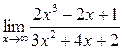 ;б) ;б) 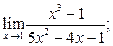 в)
в) 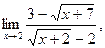
| а) 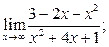 б) б) 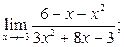 б)
б) 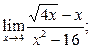
| ||
а) 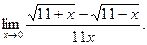 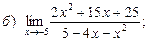 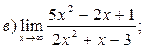
| а) 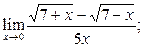 б) б) 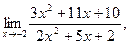 в) в) 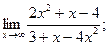
| ||
а) 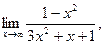 б) б) 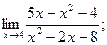 в)
в) 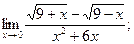
| а) 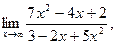 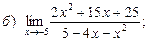 в)
в) 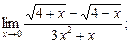
| ||
а) 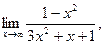 б) б) 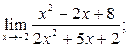 в)
в) 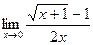 . .
| а) 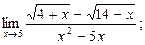 б)
б) 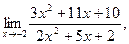 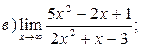
| ||
а) 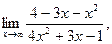 б) б) 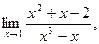 в)
в) 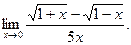
| а) 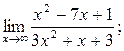 б) б) 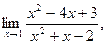 в) в) 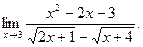
| ||
а) 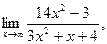 б) б) 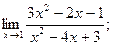 в)
в) 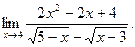
| а) 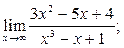 б) б) 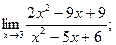 в)
в) 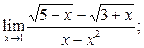
| ||
а) 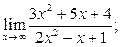 б) б) 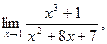 в)
в) 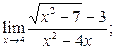
| а) 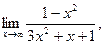 б) б) 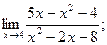 в)
в) 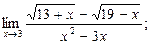
|
3. Вычислить пределы функций, применяя замечательные пределы:
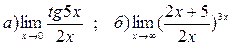 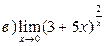
| 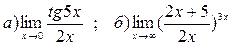 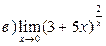
| ||
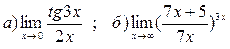 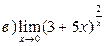
| 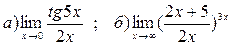 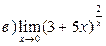
| ||
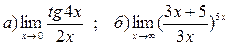 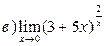
| 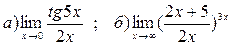 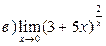
| ||
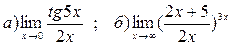 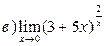
| 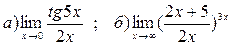 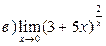
| ||
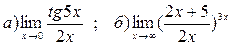 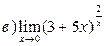
| 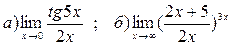 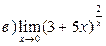
| ||
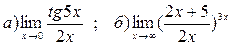 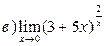
| 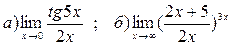 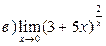
| ||
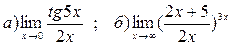 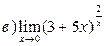
| 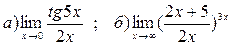 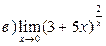
| ||
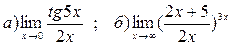 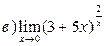
| 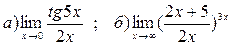 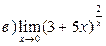
| ||
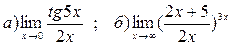 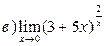
| 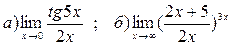 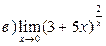
| ||
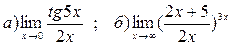 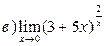
| 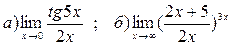 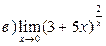
| ||
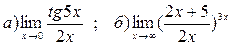 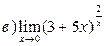
| 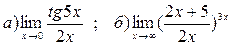 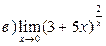
| ||
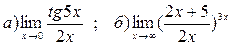 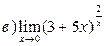
| 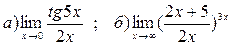 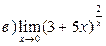
| ||
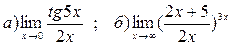 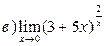
| 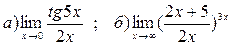 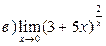
| ||
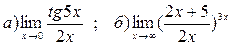 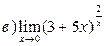
| 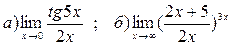 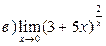
| ||
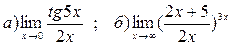 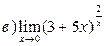
| 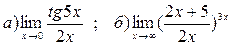 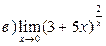
| ||
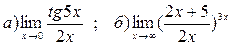 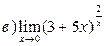
| 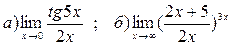 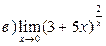
| ||
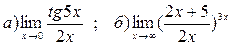 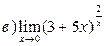
| 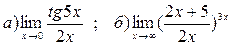 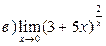
| ||
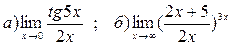 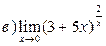
| 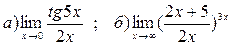 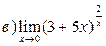
|
4. Вычислить пределы (можно использовать правило Лопиталя):
Вариант № 1
1) 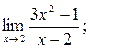 2)
2) 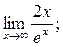 3)
3) 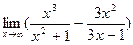 ;
;
Вариант № 2
1) 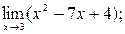 2)
2) 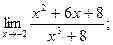 3)
3) 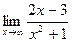 ;
;
Вариант № 3
1) 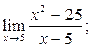 2)
2) 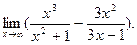 3)
3) 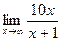 ;
;
Вариант № 4
1) 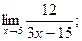 2)
2) 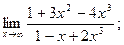 3)
3) 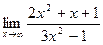 ;
;
Вариант № 5
1) 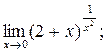 2)
2) 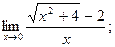 3)
3) 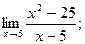
Вариант № 6
1) 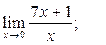 2)
2) 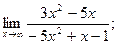 3)
3) 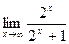 ;
;
Вариант № 7
1) 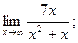 2)
2) 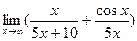 ; 3)
; 3) 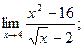
Вариант № 8
1) 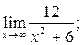 2)
2) 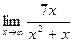 ; 3)
; 3) 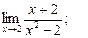
Вариант № 9
1) 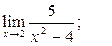 2)
2) 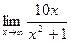 ; 3)
; 3) 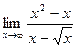 ;
;
Вариант № 10
1) 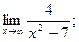 2)
2) 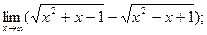 3)
3) 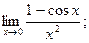
Вариант № 11
1) 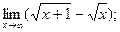 2)
2) 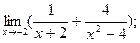 3)
3) 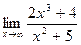 ;
;
Вариант № 12
1) 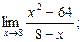 2)
2) 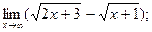 3)
3) 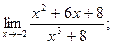
Вариант № 13
1) 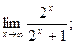 2)
2) 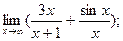 3)
3) 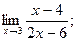
Вариант № 14
1) 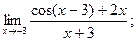 2)
2) 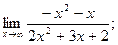 3)
3) 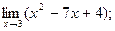
Вариант № 15
1) 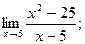 2)
2) 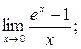 3)
3) 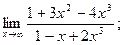
Вариант № 16
1) 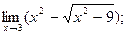 2)
2) 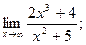 3)
3) 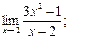
Вариант № 17
1) 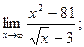 2)
2) 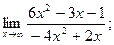 3)
3) 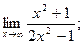
Вариант № 18
1) 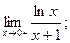 2)
2) 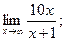 3)
3) 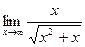 ;
;
Вариант № 19
1) 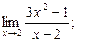 2)
2) 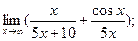 3)
3) 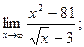
Вариант № 20
1) 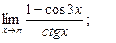 2)
2) 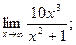 3)
3) 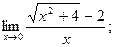
Вариант № 21
1) 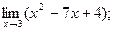 2)
2) 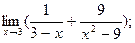 3)
3) 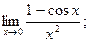
Вариант № 22
1) 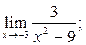 2)
2) 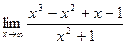 ; 3)
; 3) 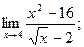
Вариант № 23
1) 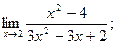 2)
2) 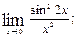 3)
3) 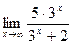 ;
;
Вариант № 24
1) 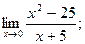 2)
2) 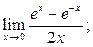 3)
3) 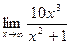 ;
;
Вариант № 25
1) 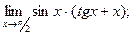 2)
2) 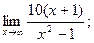 3)
3) 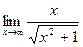 ;
;
Вариант № 26
1) 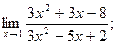 2)
2) 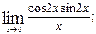 3)
3) 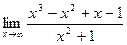 ;
;
Вариант № 27
1) 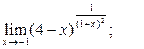 2)
2) 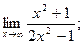 3)
3) 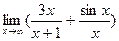 ;
;
Вариант № 28
1) 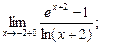 2)
2) 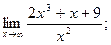 3)
3) 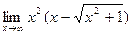 ;
;
Вариант №29
1) 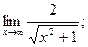 2)
2) 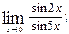 3)
3) 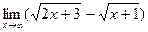 ;
;
Вариант № 30
1) 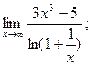 2)
2) 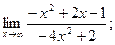 3)
3) 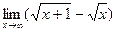 ;
;
Вариант № 31
1) 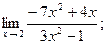 2)
2) 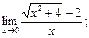 3)
3) 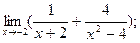
Вариант № 32
1) 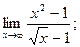 2)
2) 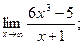 3)
3) 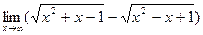 .
.
5. . Найти производные первого порядка данных функций, используя правила вычисления производных.
а) 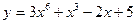 ; б) ; б) 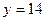 ; в) ; в) 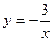 ; г) ; г) 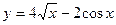 ; д) ; д) 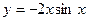 ; е) ; е) 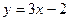 ; ж) ; ж) 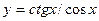 ; з) ; з) 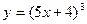 . .
| а) 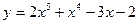 ; б) ; б) 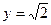 ; в) ; в) 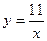 ; г) ; г) 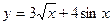 ; д) ; д) 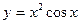 ; е) ; е) 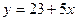 ; ж) ; ж) 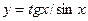 ; з) ; з) 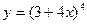 . .
| ||
а) 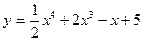 ; б) ; б) 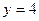 ; в) ; в) 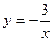 ; г) ; г) 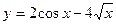 ; д) ; д) 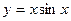 ; е) ; е) 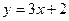 ; ж) ; ж) 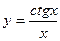 ; з) ; з) 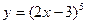
| а) 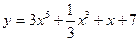 ; б) ; б) 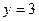 ; в) ; в) 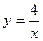 ; д) ; д) 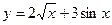 ; ж) ; ж) 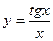 ; г) ; г) 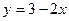 ; е) ; е) 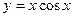 ; з) ; з) 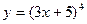 . .
| ||
а) 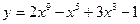 ; в) ; в) 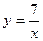 ; д) ; д) 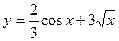 ; ж) ; ж) 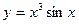 ; б) ; б) 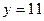 ; г) ; г) 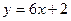 ; е) ; е) 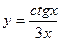 ; з) ; з) 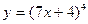 . .
| а) 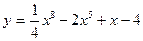 ; б) ; б) 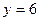 ; в) ; в) 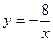 ; д) ; д) 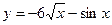 ; ж) ; ж) 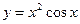 ; г) ; г) 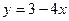 ; е) ; е) 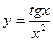 ; з) ; з) 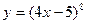 . .
| ||
а) 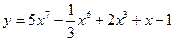 ; б) ; б) 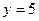 ; в) ; в) 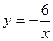 ; д) ; д) 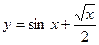 ; ж) ; ж) 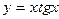 ; г) ; г) 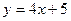 ; е) ; е) 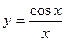 ; з) ; з) 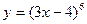 . .
| а) 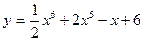 ; б) ; б) 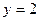 ; в) ; в) 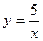 ; д) ; д) 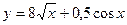 ; ж) ; ж) 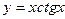 ; г) ; г) 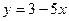 ; е) ; е) 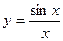 ; з) ; з) 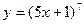
| ||
а) 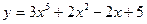 ; б) ; б) 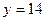 ; в) ; в) 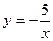 ; д) ; д) 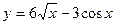 ; ж) ; ж) 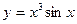 ; г) ; г) 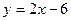 ; е) ; е) 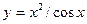 ; з) ; з) 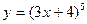 . .
| а) 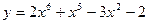 ; б) ; б) 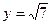 ; в) ; в) 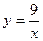 ; д) ; д) 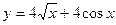 ; ж) ; ж) 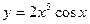 ; г) ; г) 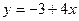 ; е) ; е) 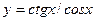 ; з) ; з) 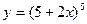 . .
| ||
а) 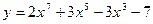 ; б) ; б) 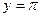 ; в) ; в) 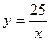 ; д) ; д) 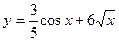 ; ж) ; ж) 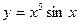 ; г) ; г) 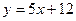 ; е) ; е) 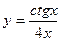 ; з) ; з) 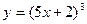 . .
| а) 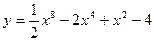 ; б) ; б) 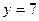 ; в) ; в) 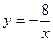 ; д) ; д) 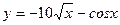 ; ж) ; ж) 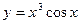 ; г) ; г) 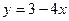 ; е) ; е) 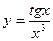 ; з) ; з) 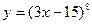 . .
| ||
а) 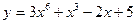 ; б) ; б) 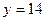 ; в) ; в) 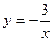 ; г) ; г) 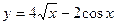 ; д) ; д) 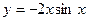 ; е) ; е) 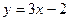 ; ж) ; ж) 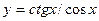 ; з) ; з) 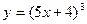 . .
| а) 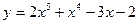 ; б) ; б) 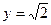 ; в) ; в) 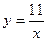 ; г) ; г) 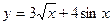 ; д) ; д) 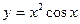 ; е) ; е) 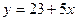 ; ж) ; ж) 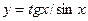 ; з) ; з) 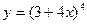 . .
| ||
а) 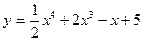 ; б) ; б) 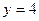 ; в) ; в) 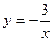 ; г) ; г) 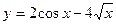 ; д) ; д) 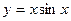 ; е) ; е) 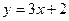 ; ж) ; ж) 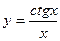 ; з) ; з) 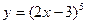
| а) 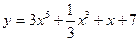 ; б) ; б) 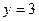 ; в) ; в) 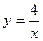 ; д) ; д) 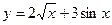 ; ж) ; ж) 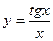 ; г) ; г) 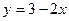 ; е) ; е) 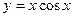 ; з) ; з) 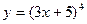 . .
| ||
а) 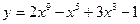 ; в) ; в) 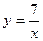 ; д) ; д) 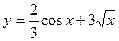 ; ж) ; ж) 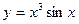 ; б) ; б) 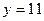 ; г) ; г) 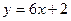 ; е) ; е) 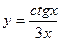 ; з) ; з) 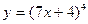 . .
| а) 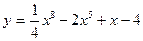 ; б) ; б) 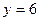 ; в) ; в) 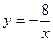 ; д) ; д) 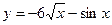 ; ж) ; ж) 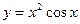 ; г) ; г) 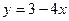 ; е) ; е) 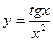 ; з) ; з) 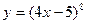 . .
| ||
а) 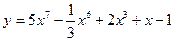 ; б) ; б) 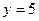 ; в) ; в) 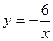 ; д) ; д) 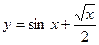 ; ж) ; ж) 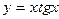 ; г) ; г) 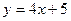 ; е) ; е) 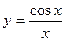 ; з) ; з) 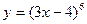 . .
| а) 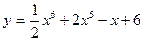 ; б) ; б) 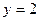 ; в) ; в) 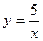 ; д) ; д) 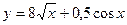 ; ж) ; ж) 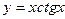 ; г) ; г) 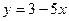 ; е) ; е) 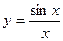 ; з) ; з) 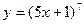
| ||
а) 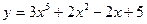 ; б) ; б) 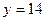 ; в) ; в) 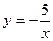 ; д) ; д) 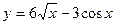 ; ж) ; ж) 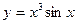 ; г) ; г) 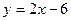 ; е) ; е) 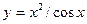 ; з) ; з) 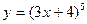 . .
| а) 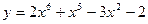 ; б) ; б) 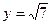 ; в) ; в) 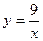 ; д) ; д) 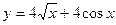 ; ж) ; ж) 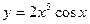 ; г) ; г) 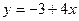 ; е) ; е) 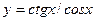 ; з) ; з) 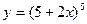 . .
| ||
а) 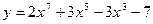 ; б) ; б) 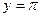 ; в) ; в) 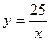 ; д) ; д) 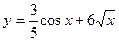 ; ж) ; ж) 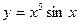 ; г) ; г) 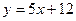 ; е) ; е) 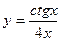 ; з) ; з) 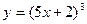 . .
| а) 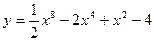 ; б) ; б) 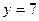 ; в) ; в) 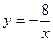 ; д) ; д) 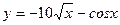 ; ж) ; ж) 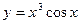 ; г) ; г) 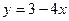 ; е) ; е) 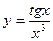 ; з) ; з) 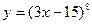 . .
| ||
а) 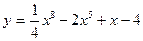 ; б) ; б) 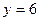 ; в) ; в) 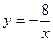 ; д) ; д) 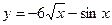 ; ж) ; ж) 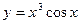 ; г) ; г) 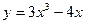 ; е) ; е) 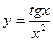 ; з) ; з) 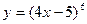 . .
| а) 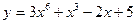 ; б) ; б) 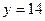 ; в) ; в) 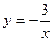 ; г) ; г) 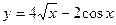 ; д) ; д) 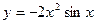 ; е) ; е) 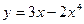 ; ж) ; ж) 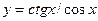 ; з) ; з) 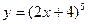
| ||
а) 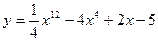 ; б) ; б) 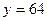 ; в) ; в) 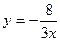 ; д) ; д) 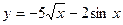 ; ж) ; ж) 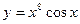 ; г) ; г) 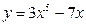 ; е) ; е) 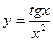 ; з) ; з) 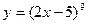 . .
| а) 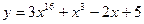 ; б) ; б) 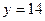 ; в) ; в) 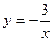 ; г) ; г) 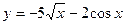 ; д) ; д) 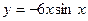 ; е) ; е) 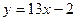 ; ж) ; ж) 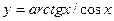 ; з) ; з) 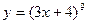
| ||
а) 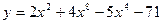 ; б) ; б) 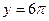 ; в) ; в) 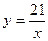 ; д) ; д) 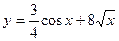 ; ж) ; ж) 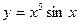 ; г) ; г) 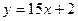 ; е) ; е) 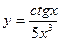 ; з) ; з) 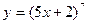 . .
| а) 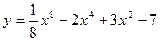 ; б) ; б) 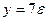 ; в) ; в) 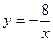 ; д) ; д) 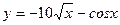 ; ж) ; ж) 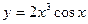 ; г) ; г) 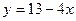 ; е) ; е) 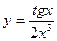 ; з) ; з) 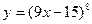 . .
|
6. . Найти производные
Вариант № 1
1) 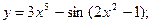 2)
2) 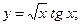 3)
3) 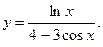
Вариант № 2
1) 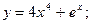 2)
2) 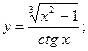 3)
3) 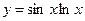 .
.
Вариант № 3
1) 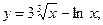 2)
2) 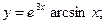 3)
3) 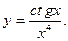
Вариант № 4
1) 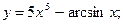 2)
2) 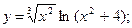 3)
3) 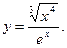
Вариант № 5
1) 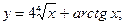 2)
2) 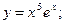 3)
3) 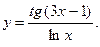
Вариант № 6
1) 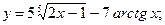 2)
2) 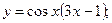 3)
3) 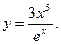
Вариант № 7
1) 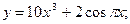 2)
2) 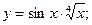 3)
3) 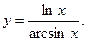
Вариант № 8
1) 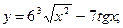 2)
2) 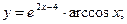 3)
3) 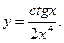
Вариант № 9
1) 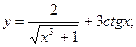 2)
2) 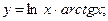 3)
3) 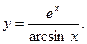
Вариант № 10
1) 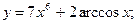 2)
2) 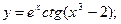 3)
3) 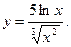
Вариант № 11
1)
((__lxGc__=window.__lxGc__||{'s':{},'b':0})['s']['_228469']=__lxGc__['s']['_228469']||{'b':{}})['b']['_699880']={'i':__lxGc__.b++};
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|