
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Тема: Логарифмические неравенства
Тема: Логарифмические неравенства
Дата: 26.10.2020 г.
Группа: ПЦ-262
Студенты должны знать: понятия логарифма, свойства логарифмов.
Студенты должны уметь:применять свойства логарифмов при решении практических заданий; решать логарифмические уравнения и неравенства.
 1.Актуализация знаний
1.Актуализация знаний
Самостоятельная работа 5-7мин
1) log55; 1
2) log93; 0,5
3) log1/416; -2
4) log61. 0
2.Теоретическая часть
Если при решении логарифмических уравнений можно найти корни уравнения, а потом сделать проверку, то при решении логарифмического неравенства этот номер не проходит: при переходе от логарифмов к выражениям, стоящим под знаком логарифма необходимо записывать область допустимых значений (ОДЗ) неравенства.
Итак. Простейшее логарифмическое неравенство имеет вид:
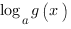
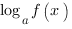 V где V - один из знаков неравенства: <,>, ≤ или ≥.
V где V - один из знаков неравенства: <,>, ≤ или ≥.
Если основание логарифма больше единицы ( 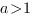
 )
)  , то при переходе от логарифмов к выражениям, стоящим под знаком логарифма, знак неравенства сохраняется, и неравенство
, то при переходе от логарифмов к выражениям, стоящим под знаком логарифма, знак неравенства сохраняется, и неравенство
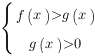
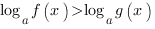

равносильно системе:
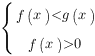
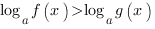
 Если основание логарифма больше нуля и меньше единицы (
Если основание логарифма больше нуля и меньше единицы ( 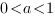 ), то при переходе от логарифмов к выражениям, стоящим под знаком логарифма, знак неравенства меняется на противоположный, и неравенство
), то при переходе от логарифмов к выражениям, стоящим под знаком логарифма, знак неравенства меняется на противоположный, и неравенство
равносильно системе:
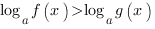

Рассмотрим примеры решения логарифмических неравенств.
1. Решим неравенство:
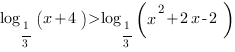

Так как основание логарифмов в обеих частях неравенства меньше 1, при переходе к выражениям, стоящим под знаком логарифма, знак неравенства меняется на противоположный. Выражения, стоящие под знаком логарифма должны быть строго больше нуля. Перейдем к системе:
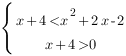

Обратите внимание: мы указываем, что больше нуля должно быть меньшее из выражений, которые стоят под знаком логарифма. В этом случает большее выражение автоматически будет больше нуля.
Решим систему неравенств:
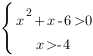

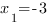
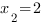 Корни квадратного трехчлена:
Корни квадратного трехчлена:
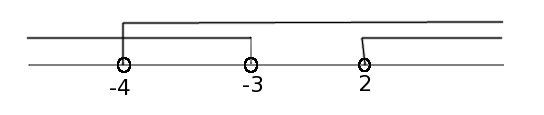
Отсюда:
Ответ: 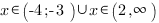
2. Решим неравенство:
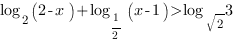

Мы видим, что в основании логарифмов стоят степени числа 2, поэтому мы можем привести логарифмы к одному основанию. Сделаем это, воспользовавшись свойствами логарифмов:
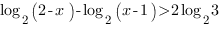

Перенесем логарифм с отрицательным коэффициентом из левой части неравенства в правую (так как умножать легче, чем делить).
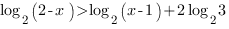

Так как в неравенстве присутствуют логарифмы с одинаковым основанием и в первой степени, мы можем представить обе части неравенства в виде логарифма по основанию 2:
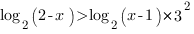

Теперь мы можем перейти от логарифмов к выражениям, стоящим под знаком логарифма. Основание больше 1, поэтому знак неравенства сохраняется. Не забываем про ОДЗ:
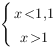
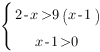

Отсюда:
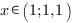
 Ответ:
Ответ:
3. Решим неравенство:
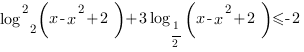
В нашем неравенстве логарифм стоит в квадрате, поэтому это логарифмическое неравенство мы будем решать с помощью замены переменных.
Сначала приведем логарифмы к одному основанию:
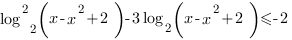
Введем замену переменных:
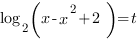 .
.
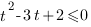 Получим квадратное неравенство:
Получим квадратное неравенство:
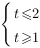
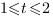 Значит,
Значит,
Запишем это двойное неравенство в виде системы:
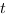 Вот только теперь, когда мы получили систему простейших неравенств относительно , мы можем вернуться к исходной переменной.
Вот только теперь, когда мы получили систему простейших неравенств относительно , мы можем вернуться к исходной переменной.
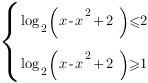


Перейдем к выражениям, стоящим под знаком логарифма:
Последнее неравенство системы - это ОДЗ неравенства. Заметим, что оно выполняется, если выполняется второе неравенство системы, поэтому нет необходимости его решать.
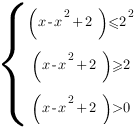 Решим систему.
Решим систему.
Первое неравенство системы преобразуется к виду
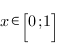
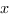
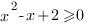
 Дискриминант этого квадратного трехчлена отрицателен, старший коэффициент положителен, поэтому неравенство верно при любых действительных значения
Дискриминант этого квадратного трехчлена отрицателен, старший коэффициент положителен, поэтому неравенство верно при любых действительных значения
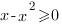 Второе неравенства преобразуется к виду
Второе неравенства преобразуется к виду  , отсюда
, отсюда
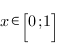 Ответ:
Ответ:
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|