
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Самостоятельно. Записать числа в тригонометрической форме.. САМОСТОЯТЕЛЬНО. Перевести в тригонометрическую и показательную форму
Изобразить комплексное число точкой на плоскости, найти модуль и аргумент, записать число в тригонометрической и показательной формах:
5. 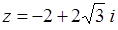
| 6. 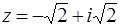
| 7. 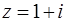
|
8. 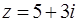
| 9. 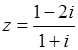
| 10. 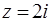
|
11. 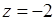
|
Примеры.
1. Найти сумму комплексных чисел z1= 2 – i и z2= –4 + 3i.
z1+ z2= ( 2 + (–1)∙i )+ (–4 + 3i ) = ( 2 + (–4)) + ((–1) + 3 ) i = –2+2i.
2. Найти произведение комплексных чисел z1= 2 – 3i и z2= –4 + 5i.
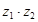 = ( 2 – 3i ) ∙ (–4 + 5i ) = 2 ∙(–4) + (-4) ∙(–3i)+ 2∙5i – 3i∙5i =7+22i.
= ( 2 – 3i ) ∙ (–4 + 5i ) = 2 ∙(–4) + (-4) ∙(–3i)+ 2∙5i – 3i∙5i =7+22i.
3. Найти частное z от деления z1= 3 – 2на z2 = 3 – i.
z = 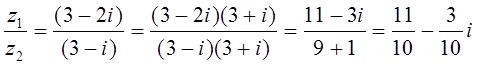 .
.
Самостоятельно
Найти сумму, разность, произведение, частного чисел:
z1= 2 + i и z2= 2 - 3i
и построить комплексные числа и их действия на плоскости.
5. Вычислить: i2, i3, i4, i5, i6, i-1 , i-2.
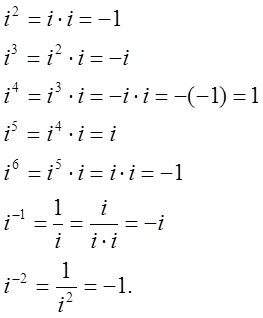
Самостоятельно Вычислить i20+i13
Примеры:
1. Найти модуль комплексных чисел z1 = 4 – 3i и z2 = –2–2i.
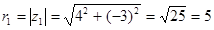 ;
;
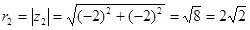 .
.
3. Найти модуль и аргумент чисел: 1) 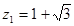 ; 2)
; 2) 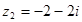 .
.
1) 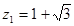 ; а = 1, b =
; а = 1, b = 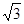 Þ
Þ 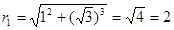 ,
,
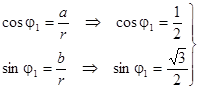 Þ j1 =
Þ j1 = 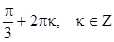 .
.
2) z2 = –2 – 2i; a = –2, b = -2 Þ 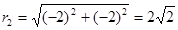 ,
,
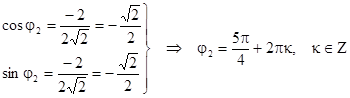 .
.
Указание: при определении главного аргумента воспользуйтесь комплексной плоскостью.
Используя формулы 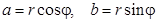 можно перейти от алгебраической формы записи комплексных чисел к тригонометрической форме (формула Муавра):
можно перейти от алгебраической формы записи комплексных чисел к тригонометрической форме (формула Муавра):
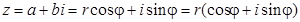 .
.
Комплексные числа в тригонометрической форме равны тогда и только тогда, когда равны их модули, а аргументы отличаются на целое число кратное 2p.
4. Записать числа в тригонометрической форме.
1) 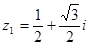 ,
,
1) 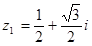 ,
, 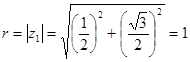 ,
,
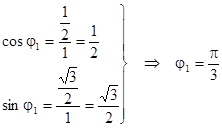 .
.
(За значение угла берем наименьшее неотрицательное из возможных значений аргумента.)
Таким образом: z1 = 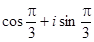 .
.
САМОСТОЯТЕЛЬНО
Перевести в тригонометрическую и показательную форму
2) 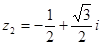 ,
,
3) 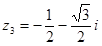 ,
,
4) 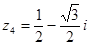 .
.
2) Вычислить: 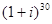 . Применяем формулу МУАВРА
. Применяем формулу МУАВРА
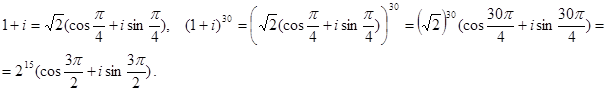
Самостоятельно Вычислить:
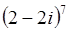
| 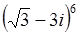
|
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|