Контакты

Случайная статья

Тема урока: «Показательные уравнения и системы. Основные приемы их решения»

Задание: изучить по конспекту, видеофильму и учебнику: § 12и § 14 способы решения показательных уравнений и систем уравнений, выполнить упражнения на закрепление материала и домашнее задание.

Урок

Тема урока: «Показательные уравнения и системы. Основные приемы их решения»

Цели урока: научиться решать показательные уравнения и системы уравнений.

Ход урока

1. Изучение нового материала.

Уравнение, в котором неизвестное содержится в показателе степени, считается показательным. Рассмотрим основные виды показательных уравнений.

ü Элементарные показательные уравнения. Эти уравнения сводятся к решению уравнений вида а^х = а^в, где а >0, а ≠ 1. При этом используется свойство степени.

Пример 1. ( 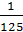)^{0,2 х + 1}= 25;

5^{– 3 (0,2 х + 1)} = 5²;

- 0,6 х – 3 = 2;

- 0,6 х = 5;

х = - 8 .

Ответ: - 8 .

Пример 2. 36 · 6^х = 1;

6^{2 + х} = 6⁰;

2 + х = 0;

х = - 2.

Ответ: - 2.

Пример 3. 27^х · 2^3х = 36;

3^3х · 2^3х = 6²;

6^3х = 6²;

3х = 2;

х = .

Ответ: .

Пример 4. 2^{х – 3} = 3^{х – 3};

х – 3 = 0;

х = 3.

Ответ: 3.

В более сложных уравнениях наша задача привести и к простейшему виду. Для этого используем следующие способы решения.

ü Вынесение общего множителя за скобки.

ü Пример 1. 2 · 3^{х + 1} – 6 · 3^{х – 1} – 3^х = 9;

3^х(2 · 3 – 6 · 3^{- 1} – 1) = 9;

3^х· 3 = 9;

3^х = 3;

х = 1.

Ответ: 1.

Пример 2. 5^2х – 7^х- 5^2х · 17 + 7^х · 17 = 0;

5^2х - 5^2х · 17 = 7^х - 7^х · 17;

5^2х(1 – 17) = 7^х(1 – 17);

- 16· 5^2х = - 16 · 7^х;

5^2х = 7^х;

25^х = 7^х;

х= 0.

Ответ: 0.

ü Сведение к квадратному уравнению или способ замены переменной.

Пример. 3 · 81^х – 8 · 9^х = 3;

3 · 81^х – 8 · 9^х – 3 = 0;

Замена 9^х = t, t > 0;

3 t² - 8 t – 3 = 0;

D = 64 +36 = 100;

t₁ = 3,

t₂ = - – не удовлетворяет условию t > 0;

9^х = 3;

3^2х = 3;

2х = 1;

х= 0,5.

Ответ: 0,5.

ü Решение однородного показательного уравнения.

Пример. 4·3^x-9·2^x=0, это уравнение однородное,

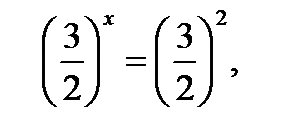
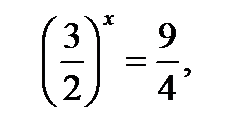
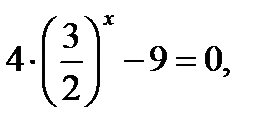так как 2^x≠0, то, разделив уравнение на 2^x, получим

Мы применили способ почленного деления уравнения. Ответ: 2

ü Графический способ решения.

Пример. Решить уравнение: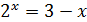

Пусть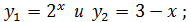

Строим графики этих функций и находим точку пересечения графиков.

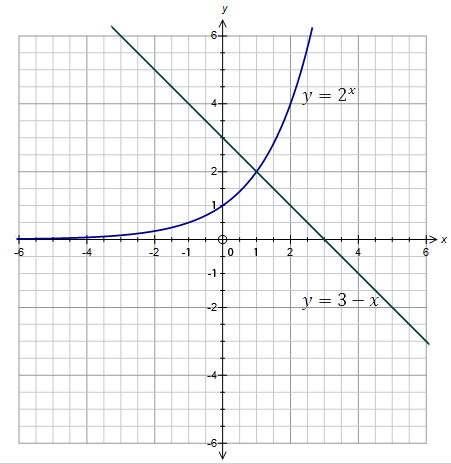
Точка пересечения имеет координаты 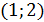. Абсцисса точки пересечения графиков функций x=1 является корнем уравнения. 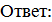1.

ü Решим систему уравнений:

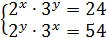
Решение:

Преобразуем правые части уравнений системы:

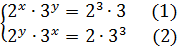
1) Перемножим уравнения (1) и (2):

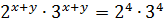
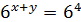
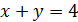
2) Поделим уравнения (1) и (2):

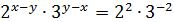
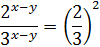
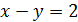
3) Данную систему сводим к равносильной ей системе:

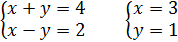
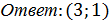
2. Для закрепления изученного материала решите следующие уравнения:

1. 400^х = ;

2. 3 · 9^х = 81

3. 2^{х + 1} + 2^{х – 1} + 2^х = 28

4. 9^х – 4 · 3^х + 3 = 0

5. 3^{х + 4} + 5^{х + 3} · 3 = 5^{х + 4} + 3^{х + 3}

3. Домашнее задание:§ 12, № 240

© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.