
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Остатки и модули.
Остатки и модули.
1) В вершинах n-угольника стоят числа 1 и –1. На каждой стороне написано произведение чисел на её концах. Оказалось, что сумма чисел на сторонах равна нулю. Доказать, что a) n чётно; б) n делится на 4.
2) В комнате стоят трёхногие табуретки и четвероногие стулья. Когда на все эти сидячие места уселись люди, в комнате оказалось 39 ног.
Сколько в комнате табуреток?
3) Найти все прямоугольники с натуральными сторонами, у которых периметр равен площади.
4)Решить в целых числах уравнение: 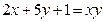
5)Фокусник вручает вам конверт с листочком и просит вас задумать натуральное число 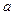 . Затем (не зная ваше число) сообщает вам число
. Затем (не зная ваше число) сообщает вам число 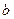 . Потом он просит вас посчитать
. Потом он просит вас посчитать 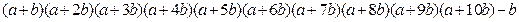
и записать на листочке последнюю цифру полученного числа. После чего зритель открывает конверт и видит, что там записана та же цифра. Каким образом удается этот фокус?
6) В строку выписано 1000 натуральных чисел. За один ход можно прибавить по единице к некоторым n из этих чисел. Всегда ли такими операциями можно сделать все числа равными?
а) 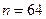 ; б)
; б) 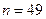 .
.
7)На столе лежит кучка из 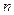 камней. Двое по очереди берут за ход или один камень, или количество камней, равное какому-то простому делителю
камней. Двое по очереди берут за ход или один камень, или количество камней, равное какому-то простому делителю 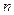 . Выигрывает взявший последний камень. При каких
. Выигрывает взявший последний камень. При каких 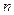 первый игрок может выиграть независимо от действий оппонента?
первый игрок может выиграть независимо от действий оппонента?
(турнир городов, базовый тур, 8-9 класс, никто не решил у нас =( )
8) Решить в натуральных числах 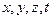 уравнение
уравнение
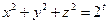
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|