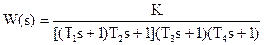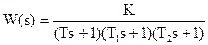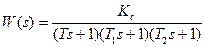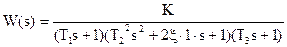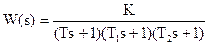ТЮМЕНСКИЙ ГОСУДАРСТВЕННЫЙ НЕФТЕГАЗОВЫЙ УНИВЕРСИТЕТ

ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ

ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ

ТЮМЕНСКИЙ ГОСУДАРСТВЕННЫЙ НЕФТЕГАЗОВЫЙ УНИВЕРСИТЕТ

ИНСТИТУТ НЕФТИ И ГАЗА

Кафедра Кибернетических систем

Методические указания

к лабораторной работе № 7

по дисциплине «Теория автоматического управления»

на тему «Метод D-разбиения»

Тюмень 2007

1.Цель работы: построить кривую D-разбиения по заданным параметрам для приведенной системы управления.

2.Теоритические сведения.

При исследовании устойчивости системы большое практическое значение имеет построение областей устойчивости в плоскости одного или двух параметров системы. Разбиение пространства коэффициентов на области устойчивости и неустойчивости называется D-разбиением. Переход в пространстве коэффициентов через границу D-разбиения соответствует переходу в плоскости корней через мнимую ось. Таким образом, граница D-разбиения есть отображение мнимой оси плоскости корней на пространство коэффициентов характеристического уравнения.

2.1. D-разбиение плоскости одного комплексного параметра.

Пусть определяется влияние на устойчивость системы параметра 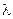. Приведем характеристическое уравнение замкнутой системы к виду:

P(p)+ 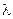R(p) = 0,

где 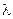- исследуемый параметр, а P(p) – полином, не содержащий этот параметр.

Подставим вместо p значение 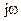. Это позволит отобразить мнимую ось плоскости корней p на плоскость комплексного коэффициента ( ).

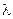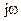Запишем уравнение границы D-разбиения:

P( 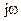)+ 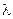R( 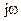) = 0.

Выразим из полученного уравнения параметр 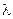и выделим реальную и мнимую часть выражения:

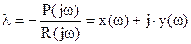Изменяя частоту w от 0 до + ¥, вычислим 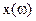и 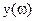, и по ним построим половину границы D-разбиения. Пространство коэффициентов представляется системой координат X-Y (рис.1а). Зеркально отображая полученную кривую относительно действительной оси построим вторую половину границы. Затем необходимо наметить предполагаемую область устойчивости. Для этого необходимо применить правило штриховки: нужно двигаться по кривой разбиения от -¥ до +¥ и штриховать слева. Переходу корня в плоскости корней из штрихованной полуплоскости в нештрихованную вдоль стрелки1 соответствует аналогичный переход через границу D-разбиения вдоль стрелки 1, и наоборот (рис. 1б). Полученная кривая должна охватывать участок действительной положительной оси, т.к. реально число 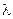- действительное.

Рисунок 1

Если известно количество правых корней, соответствующее хотя бы одной D-области, то двигаясь от нее через границы с учетом штриховок, можно обозначить все остальные области. Если пересечение границы происходит по направлению штриховки, то один корень в плоскости D-разбиения переходит из правой полуплоскости в левую; если против штриховки, то один корень переходит из левой полуплоскости в правую. Область с наибольшим количеством штриховок является претендентом на область устойчивости. Нужно взять любую точку из этой области и при соответствующем значении 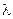проверить систему на устойчивость любым методом.

Для линейных задач определяют вещественный диапазон изменения параметра (0; 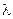кр).

2.2. D-разбиение плоскости двух параметров.

Предположим, что в характеристическом уравнении коэффициенты линейно зависят от двух параметров 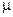и 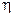так, что характеристическое уравнение можно привести к виду:

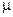Р (р) + 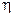Q (р) + R (р) = 0 ,

где: 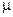и 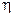- искомые параметры, P (р); Q (р); R (р) - полиномы.

Запишем уравнение границы D-разбиения:

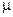Р (jw) + 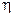Q (jw) + R (jw) = 0.

Полиномы P (р), Q (р) и R (р) могут быть разложены на реальные и мнимые части:

Р (jw) = Р₁ (w) + j Р₂ (w)

Q (jw) = Q₁ (w) + j Q₂ (w)

R (jw) = R₁ (w) + j R₂ (w)

Подставив выражения и сгруппировав реальные и мнимые части получим:

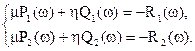
Таким образом, мы получаем два уравнения с двумя неизвестными. Чаще всего используют при этом правило Крамера:

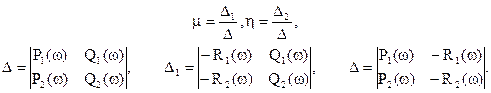
Изменяя частоту w, вычисляем соответствующие 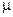(w) и 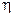(w), получая границу D-разбиения.

Штриховку границы D-разбиения выполняют по правилу:

- слева при обходе в сторону возрастающих w, если Δ > 0;

- справа при обходе в сторону возрастающих w, если Δ < 0;

- штриховка двойная, т.к. граница D-разбиения совпадает для положительных и отрицательных частот.

- особые линии (при w = 0 и w = ¥) имеют одинарную штриховку, которая должна вблизи точки сопряжения совпадать с двойной штриховкой, т.е. заштрихованные и незаштрихованные стороны обычной границы и особой линии совпадали.

Особые линии получаются при w = 0 (a_n = 0) или w → ¥ (a₀= 0).

3.Пример.

Дано характеристическое уравнение: (1 + Т₁ р) (1 + Т₂р) (1 + Т₃р) + к = 0

Т₁, Т₂, Т₃ – заданные постоянные времени; к – общий коэффициент усиления.

Решение.

Выразим из полученного уравнения искомый параметр:

к = -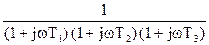

Раскрываем скобки и приводим к виду: X + jY:

к = [w² (Т₁Т₂ + Т₁Т₃ + Т₂Т₃) – 1] + j [w³ Т₁Т₂ Т₃ – w (Т₁ + Т₂ + Т₃)]

Изменяя w, построим границу D-разбиения (рис.2)

Рис.2 Граница D-разбиения

На приведенном рисунке I – область, претендующая на устойчивость; II – область, где число правых корней увеличивается на один; III – область, где число правых корней увеличивается на 2 по сравнению с I.

Определяем устойчивость при к = 0, характеристическое уравнение обращается при этом в уравнение (1 + Т1р) (1 + Т2р) (1 + Т3р) = 0. Оно имеет отрицательные корни, следовательно, система устойчива. Система устойчива при изменении к от 0 до точки Б.

Система устойчива и при отрицательных значениях к от точки А до точки 0, что соответствует положительной обратной связи.

4.Требования к оформлению отчета.

Отчет должен содержать:

- цель работы;

- задание;

- ход решения;

- рисунок границы D-разбиения

- выводы по работе.

5.Варианты заданий.

№	Передаточная функция	Т₁	Т₂	Т₃	Т₄	K_c
		0.2	0.6	0.05	0.4
		0.1	0.3	0.001	0.02
		0.5	0.1	0.05	0.1
			0.8
			0.1
			0.05
		0.1	0.6
			0.8
			0.2
		0.2		0.2
				0.5
		0.1		0.3
			0.6
			0.2
			0.1
		0.1	0.5	0.03	0.2
		0.2	0.4	0.003	0.03
		0.4	0.2	0.03	0.2
		0.2	0.5
			0.7
			0.1
		0.4		0.3
				0.4
		0.2		0.2
			0.5
			0.3
			0.2
		0.3	0.5	0.01	0.4
		0.1	0.2	0.005	0.05
		0.6	0.1	0.05	0.1