Конические сечения.

Конические сечения.

В зависимости от направления секущей плоскости в сечении конической поверхности вращения могут получиться различные линии (кривые второго порядка) – коники.

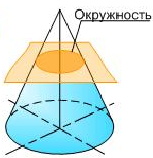
Если пересечь конус плоскостью перпендикулярной к оси конуса, то в сечении будет окружность (рис. 1а).

Если пересечь прямой круговой конус плоскостью, которая наклонена к оси конуса и пересекает все его образующие, то в сечении получится эллипс (рис. 1б).

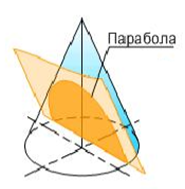
Если пересечь тот же конус плоскостью параллельной одной из его образующих, то в сечении получится парабола (рис. 1в).

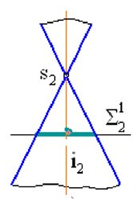
Если пересечь конус плоскостью, параллельной двум из его образующих (не проходящей через его вершину) то в сечении получится гипербола (рис. 1г).

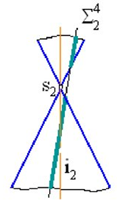
Секущая плоскость, проходящая через вершину, пересекает конус по образующим (рис. 1д).

Все сказанное, о сечениях конуса, будет справедливо и для наклонного конуса, кругового или эллиптического, т.е. для конуса поверхность которого в декартовых координатах выражается алгебраическим уравнением второй степени.

а)

б)

в)

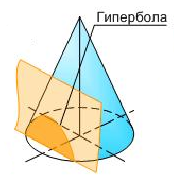
г)

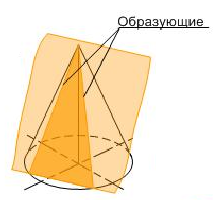
д)

Рисунок 1 – Сечения конуса – коники (а) окружность; б) эллипс; в) парабола;

г) гипербола; д) образующие)