Задание: изучить тему по плану, ответить на вопросы и решить задачу.

Гр 294 Техническая механика Лепакова 21.11.20г

Тема урока: Чистый сдвиг. Кручение.

Цель: Изучить деформации сдвига и кручения.

Задание: изучить тему по плану, ответить на вопросы и решить задачу.

План изучения темы:

1. Закон Гука при сдвиге. Модуль сдвига.

2. Внутренние силовые факторы при кручении. Эпюры крутящих моментов.

3. Кручение бруса круглого поперечного сечения.

4. Напряжения в поперечном сечении. Угол закручивания.

5. Расчеты на прочность и жесткость при кручении.

6. Расчеты цилиндрических винтовых пружин на растяжение-сжатие.

Вопросы:

1. Какая деформация называется чистым сдвигом?

2. Что называется кручением?

3. Как формулируется закон Гука при сдвиге?

4. Какие внутренние силовые факторы возникают при кручении?

5. Чему равна удельная потенциальная энергия при чистом сдвиге?

6. В результате чего происходит деформация кручения бруса круглого поперечного сечения?

7. Куда направлены напряжения в поперечных сечениях бруса при кручении?

Учебник Сафонова Г.Г., Артюховская Т.Ю., Ермаков Д.А. Техническая механика, стр. 272-292

Электронная ссылка на учебник: znanium.com, labirint.ru

Электронные ресурсы: prosopromat.ru, infourok.ru, isopromat.ru

Ответы присылать мне на электронную почту: lepakova68@mail.ru или в ВК

Критерии оценивания:

Оценка «5» ставится, если обучающийся ответил на 7 вопросов в полном объёме и верно решил задачу без ошибок;

Оценка «4» ставится, если обучающийся ответил правильно на 7 вопросов в полном объеме и решил задачу с ошибками;

Оценка «3» ставится, если обучающийся ответил правильно на 7 вопросов;

Оценка «2» ставится, если обучающийся ответил на 6 и меньше вопросов.

Образец решения задачи:

1. Определить потребное количество заклепок для передачи внешней нагрузке 120 кН.Заклепки расположить в один ряд.

Решение: Для определения потребного количества заклепок, необходимо чтобы выполнялось условие прочности при сдвиге:

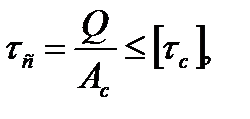
Q – поперечная сила:

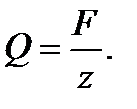
Поэтому

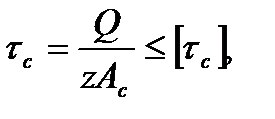
где A_c – площадь сдвига:

A_c = πr²;

z – количество заклепок.

Откуда:

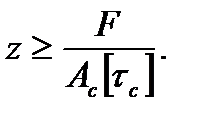
Задача для самостоятельного решения:

1. Определить потребное количество заклепок для передачи внешней нагрузке 110 кН.Заклепки расположить в один ряд.

Краткие теоретические и справочно-информационные материалы по теме:
Экспериментально чистый сдвиг может быть осуществлен при кручении тонкостенной трубы (рис. 79, а), поэтому деформация чистого сдвига отнесена к теме «кручение».
Рассмотрим элемент abcd, вырезанный из тонкостенной трубы (рис. 79, б).
При возникновении касательных напряжений элемент перекашивается. Если считать грань ad

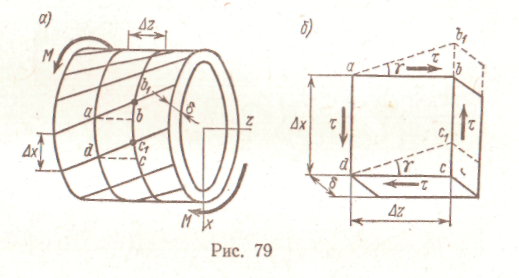
закрепленной, то грань bс сдвинется в положение b₁c₁. Прямые углы между гранями изменяются на величину γ. Угол γ , представляющий собой изменение первоначально прямого угла между гранями элементарного параллелепипеда, называется углом сдвига.
Касательные напряжения τ и угол сдвига γ, называемый также относительным сдвигом, связаны прямой пропорциональностью, то есть законом Гука:

Входящая в эту формулу величина G называется модулем сдвига. Эта величина характеризует жесткость материала при деформации сдвига. Так как γ выражается отвлеченным числом, то модуль сдвига G, как и модуль продольной упругости Е, имеет ту же единицу измерения, что и напряжение: МПа, Н/мм², кгс/см².
Между модулем упругости Е и модулем сдвига G существует зависимость, которую приводим без вывода:

где μ — коэффициент поперечной деформации (коэффициент Пуассона).

Для стали μ = 0,25; G = 0,4 Е = 0,4^.2^.10⁵ = 8^.10⁴ МПа. Приведенные соотношения между G и Е подтверждаются опытами.
Основные понятия. Эпюры крутящих моментов
На кручение обычно работают брусья круглого поперечного сечения, например валы и витки цилиндрических пружин.
Кручение возникает при нагружении бруса парами сил, расположенными в плоскостях, перпендикулярных продольной оси бруса (рис. 80).

Моменты этих пар M_вр называют вращающими моментами. Их алгебраическая сумма равна нулю, если вал находится в равновесии и вращается равномерно. Величину вращающего момента М_вр можно вычислить по передаваемой мощности Р и частоте вращения n:

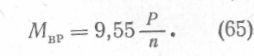
Эта формула дает величину момента в Н^.м, если мощность выражена в Вт, а частота в об/мин.

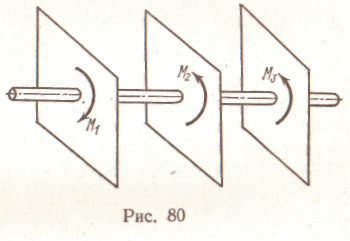
Момент внутренних сил относительно продольной оси бруса называют крутящим моментом М_к. При кручении в поперечных сечениях бруса возникает один внутренний силовой фактор — крутящий момент М_к. Он определяется при помощи метода сечений.
Когда вращение от двигателя передается при помощи передаточного вала нескольким рабочим машинам, крутящий момент не остается постоянным по длине вала. Характер изменения крутящего момента по длине вала наиболее наглядно может быть представлен эпюрой крутящих моментов. Рассмотрим построение такой эпюры для вала, на котором закреплено несколько шкивов (рис. 81, а); шкив I получает вращение от двигателя, шкивы II, III и IV передают его станкам. Моменты, передаваемые каждым шкивом на вал, вычисляют по формуле (65). Направление момента М₁ противоположно направлению моментов М₂, М₃ и M₄. При установившемся движении (равномерном вращении вала), пренебрегая трением в подшипниках, получаем из условия равновесия вала:

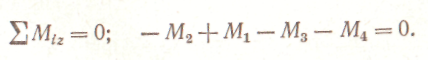
Крутящий момент изменяется в сечениях вала, передающих внешние моменты от шкивов. Разделим вал на три участка (рис. 81, а) и определим крутящие моменты в поперечных сечениях каждого из них. Крутящий момент в любом поперечном сечении первого участка между шкивами II и I уравновешивает момент внешней пары М_к1, действующий на левую отсеченную часть, т. е,

М_к ₁ = М₂.

При рассмотрении правой части из условия ее равновесия мы получили бы, естественно, тот же результат:

M_K1=М₁ – М₃ – М ₄ = М₂

Аналогично вычисляется крутящий момент в поперечных сечениях на втором участке вала между шкивами I и III

М_к2 = М₂ – М₁= – М₃ – М₄ ,

а на третьем участке между шкивами III и IV

M_к3 = М₂ – M₁ + М₃ = – М₄.

Итак, крутящий момент в каком-либо поперечном сечении вала численно равен алгебраической сумме моментов внешних пар, действующих на вал в плоскостях, перпендикулярных оси вала, и приложенных по одну сторону от рассматриваемого сечения. Эпюру крутящих моментов строят аналогично эпюре продольных сил, откладывая от горизонтали (рис. 81, б) ординаты, пропорциональные крутящим моментам в поперечных сечениях соответствующих участков вала.

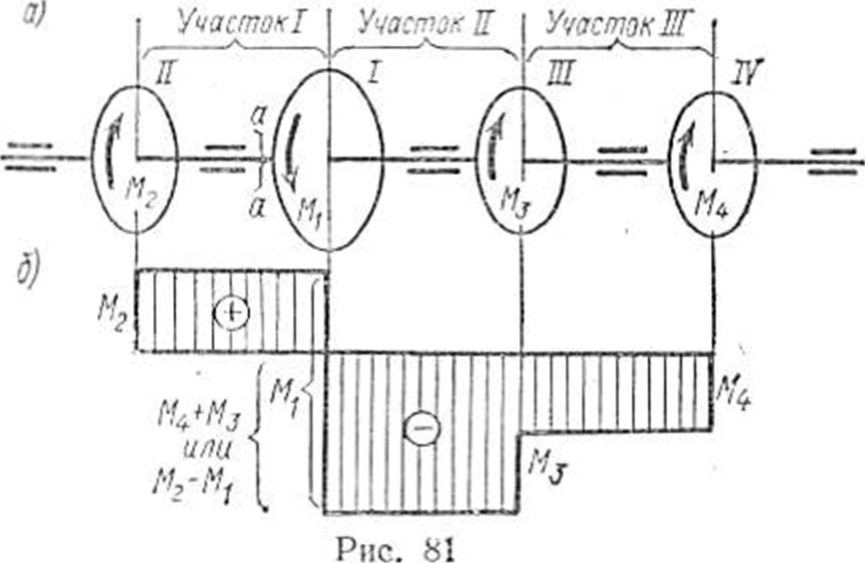
Знак крутящего момента в поперечном сечении вала определяется исходя из направления внешних моментов. Крутящий момент положителен, когда внешние моменты вращают отсеченную часть по часовой стрелке, если смотреть со стороны проведенного сечения.