Контакты

Случайная статья

Группы 519-1-2, 529, 539.. Практика 1 (неделя до 6 сентября).. Комплексные числа. Решение.

Группы 519-1-2, 529, 539.

Практика 1 (неделя до 6 сентября).

Комплексные числа

Задача 1. Умножить и поделить в алгебраической форме числа 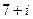и .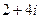

Решение. Умножим эти числа. = =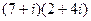

= .

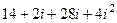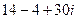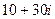Поделим, с помощью умножения на сопряжённое:

= = = = = = .

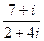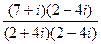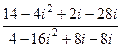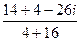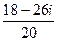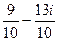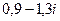Ответ. 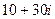и .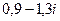

Задача 2. Умножить и поделить .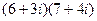

Решение. = = = .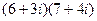

= = = = .

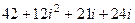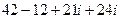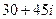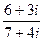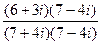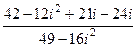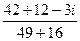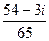Ответ. 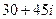и .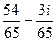

Задача 3.Разделить 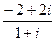тремя способами:

1) с помощью умножения на сопряжённое число

2) в тригонометрической форме.

3) в показательной форме.

Решение. 1) = = .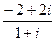

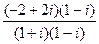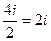2) Построим чертёж, найдём модуль и аргумент каждого из 2 чисел.

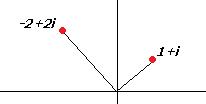
Модули ищутся по теореме Пифагора и равны 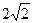и .

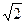Аргументы: , .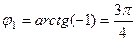

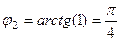Итак, .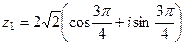

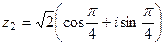Делим их модули и вычитаем аргументы.

= =

= .

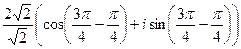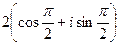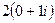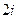3) = = = = =

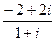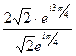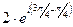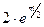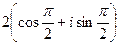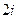
Ответ. .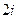

Задача 4.Умножить 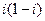тремя способами:

1) с помощью умножения на сопряжённое число

2) в тригонометрической форме.

3) в показательной форме.

Решение. 1) = = .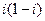

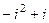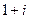2) , .

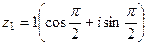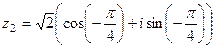Умножаются их модули и складываются аргументы.

= =

= .

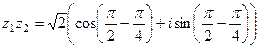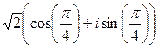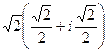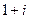3) 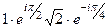= = 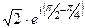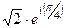, а далее раскроем по формуле Эйлера = = .

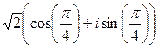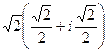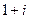Ответ. .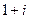

Задача 5.Вычислить в показательной форме .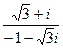

Решение.

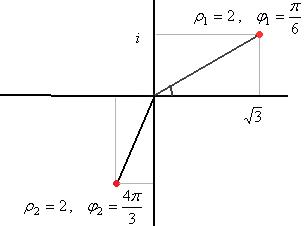
Для 1-го числа: 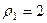, 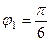(та же точка, как в прошлой задаче).

Для 2-го числа: 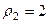, 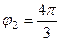. Тогда 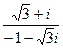= = 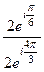= = 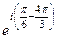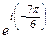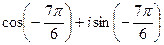, прибавим 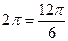, для удобства вычисления. Итак, = .

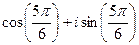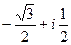Ответ. .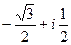

Задача 6. Возвести в степень: .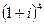

Решение.Перейдём к показательной форме, для этого сначала найдём модуль и аргумент числа 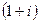с помощью чертежа. Число в 1-й четверти, угол 45 градусов.

Чертёж, показывающий, расположение 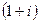на плоскости, это число выделено красным цветом:

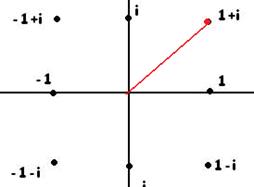
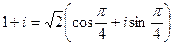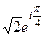= . По формуле Муавра, =

= = = = = .

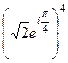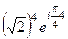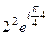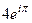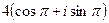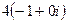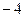Ответ. .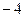

Задача 7.Возвести в степень в показательной форме: .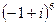

Решение. 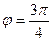, 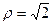. Тогда , =

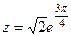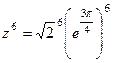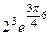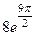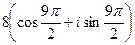= = , мы можем отбросить 1 или более полных оборотов, при этом синус и косинус не изменятся, то есть отнять 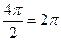, либо 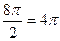. Тогда угол 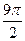эквивалентен 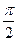, и остаётся вычислить: = = .

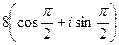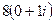Ответ .

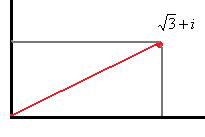
Задача 8. Возвести в степень .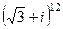

Решение. Аналогично прошлой задаче, сначала переводим в показательную форму. Угол здесь 30 градусов, то есть 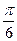, модуль 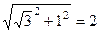. Итак, = .

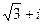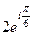Тогда = = = =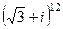

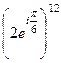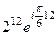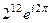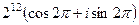
Теперь можем отнять полный оборот 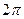, косинус и синус при этом не меняются. тогда получим = =

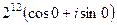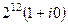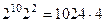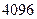= . Ответ. .

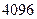Задача 9. Вычислить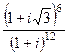

Решение.Представим каждое число в показательной форме.

, , , .

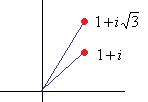
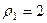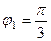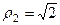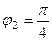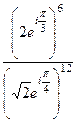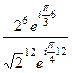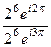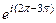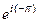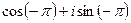= = = = = но можно произвольно прибавить 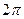, ведь от этого не изменятся синус и косинус, поэтому

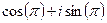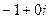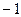= = . Ответ. .

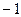Задача 10. Вычислить .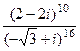

Решение.Представим в показательной форме каждое из чисел.

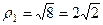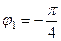, и 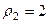, 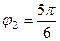. Тогда

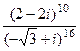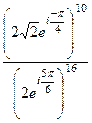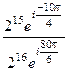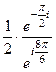= = = здесь в числителе прибавили угол 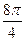, кратный 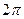, а в знаменателе отняли 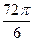. Далее, = = = = = = .

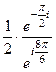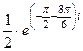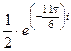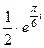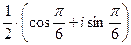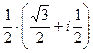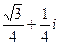Ответ. .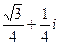

Домашняя задача. Вычислить 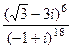. Ответ.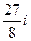

© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.