
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Решения задач 5 класс
Решения задач 5 класс
1.Разрежем на 3 части: первые 2 цифры, средняя и последние 2 цифры. перевернем число из первых 2 цифр, получим 95, перевернем последние 2 цифры, получим 68. 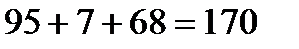 .
.
2.В кинозале не меньше 8 рядов. Сейчас когда каждое 4 кресло пустое в зале 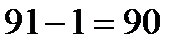 человек. В каждом ряду их поровну. Пусть сейчас
человек. В каждом ряду их поровну. Пусть сейчас
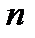 - человек в каждом ряду (не мест, а человек) и
- человек в каждом ряду (не мест, а человек) и 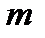 - рядов. Тогда
- рядов. Тогда
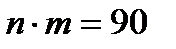 ;
;
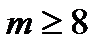 ;
; 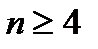 (иначе в ряду нет 4-го кресла ни одного и нечего оставлять пустым). Рассмотрим случаи:
(иначе в ряду нет 4-го кресла ни одного и нечего оставлять пустым). Рассмотрим случаи:
1) 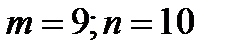 . Тогда мест в ряду
. Тогда мест в ряду 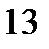 (если 2 пустых места, то не более 11 мест всего и не более 9 с учетом свободных). Но тогда
(если 2 пустых места, то не более 11 мест всего и не более 9 с учетом свободных). Но тогда 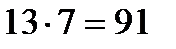 и до пандемии люди поместились бы в 7 рядов, что противоречит условию.
и до пандемии люди поместились бы в 7 рядов, что противоречит условию.
2) 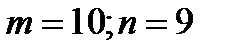 . Тогда мест в ряду 11 или 12(12-го места может не быть и 2 пустых кресла 4 и 8, или 12 место есть и 3 пустых места). Однако, если мест в ряду 11, то до пандемии в 8 рядов бы поместилось 88 человек, а надо 91. Значит, мест в ряду все же 12
. Тогда мест в ряду 11 или 12(12-го места может не быть и 2 пустых кресла 4 и 8, или 12 место есть и 3 пустых места). Однако, если мест в ряду 11, то до пандемии в 8 рядов бы поместилось 88 человек, а надо 91. Значит, мест в ряду все же 12
3) 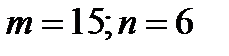 . Но тогда не больше 8 мест в ряду, и в прошлом году на них бы не поместилось 91 человек в 8 рядах, если мест в ряду еще меньше – тем более не поместились бы. Итак, все случаи разобраны.
. Но тогда не больше 8 мест в ряду, и в прошлом году на них бы не поместилось 91 человек в 8 рядах, если мест в ряду еще меньше – тем более не поместились бы. Итак, все случаи разобраны.
Ответ: в кинотеатре 10 рядов по 12 человек.
3.Предположим, что в первой табличке верхняя надпись ложная. Тогда оставшиеся 2 истинные. То есть в C смерть, в D столица, в B – не клад, значит, в B змей, в A клад. Тогда 2 табличка говорит что в C смерть (правда), прямо столица (правда), в A змей –ложь. Все выполнено пока. 3 табличка говорит, что в D столица (правда) в A смерть (ложь), в B- змей – правда. Снова ровно одно ложное. Наконец 4 табличка говорит , что в A столица (ложь),B –змей – правда, С- смерть – правда. Все условия выполнены. Значит, условию задачи не противоречит случай, когда в A – клад, в B – змей, в C – смерть, в D – столица. Но этого не достаточно. Нужно еще рассмотреть случаи, когда на первой табличке ложно второе утверждение и когда ложно третье. И найти противоречие. Сделайте это самостоятельно.
Ответ: То есть в C смерть, в D столица, в B змей, в A клад.
4)
5) Заметим, что если в итоге карточки 1 и 2 у одного и того же человека, то выиграл Петя. Действительно, 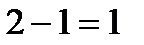 . Разность чисел 2 и 1 равна числу из того же набора (1). Тут важно, что не написано, “другому числу”.
. Разность чисел 2 и 1 равна числу из того же набора (1). Тут важно, что не написано, “другому числу”.
Итак, поймем, как надо в итоге поделить карточки, чтобы Выиграл Вася. 2 и 1 у разных людей. Аналогично 4-2=2, значит, 2 и 4 у разных людей. Значит, у одного 2, а у другого 1 и 4. Тогда так как 4-1=3, то 3 вместе с 3. Но тогда 5 некуда пожить. У первого будет 5-3=2, у второго будет 5-4=1. Значит, нельзя так поделить карточки. И значит, как бы они не играли всегда выигрывает Петя, увы.
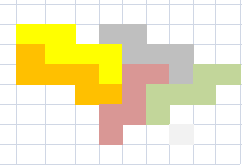
6) рассмотрим квадрат с суммой 14. 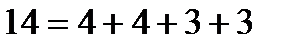 в некотором порядке(иначе никак без повторений). Может быть заполнено
в некотором порядке(иначе никак без повторений). Может быть заполнено

Как бы мы не заполнили, в каждом из строк и столбцов квадрата будет 3+4. И значит, остальные клетки можно заполнять независимо от этого квадрата (одни и те же ограничения в каждой строке и столбце при обоих способах заполнения квадрата). Поэтому, посчитаем сколько способов заполнить оставшиеся при одном из способов и умножим на 2. Это правило произведения.
Далее в нижнем уголке с суммой 5 внизу в строке 1 и 2, значит в верхней клетке 2 слева от неё 1, снизу от 1 стоит 2 и в оставшейся 1 получаем заполнение :
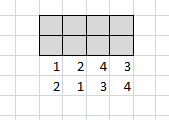
Далее наверху может быть в доминошке с 5 справа 1 или 2. В первом случае получим аналогичными рассуждениями картинку слева а во втором справа

Итак, рассмотрели все случаи и получили, что у нас всего 4 решения. На всякий приведем оставшиеся 2, когда квадратик 2 на 2 меняется:
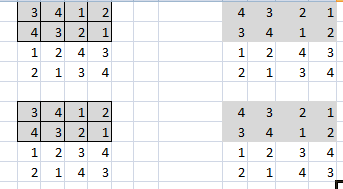
Ответ: 4 решения.
7)Будем выпишем первые 7 хороших чисел:
3,15,23,43,59,87,111.
Рассмотрим другую спиральку, в которой идут не последовательные нечетные, а все подряд натуральные, а хороший по-новому правилу будем брать на тех же местах. Тогда получим новые хорошие числа
2,8,12,22,30,44,56
Выпишем разности между соседними числами, получим
6,4,10,8,14,12,…
Заметим закономерность, что нечетные разности 6,10,14 каждый раз растут на 4. И четные тоже 4,8,12,… То есть разности
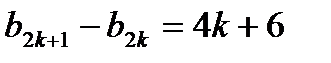 ;
; 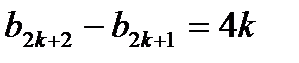
Таким образом (новое) хорошее число следующее с четным номером можно найти из соотношения
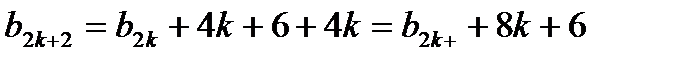 ; Значит
; Значит
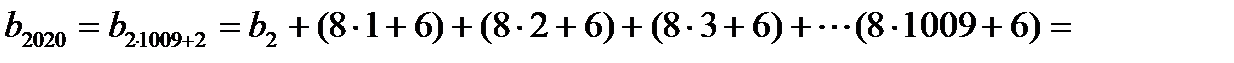
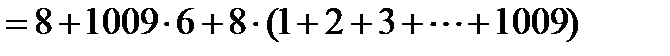 .
.
Посчитаем сумму в скобке.
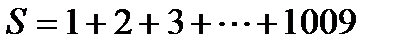 ; переставим в обратном порядке
; переставим в обратном порядке
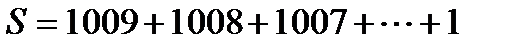 ;
;
Сложим эти две суммы по столбцам. В каждом столбце 1009+1=1010.
И всего столбцов 1009. Поэтому 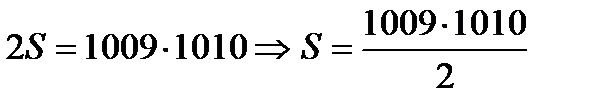 ;
;
Итак, получаем 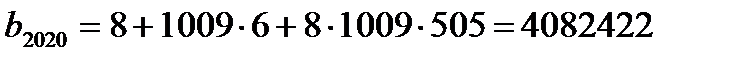 ;
;
Значит, исходное 2020-ое хорошее число равно 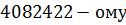 нечетному числу.
нечетному числу.
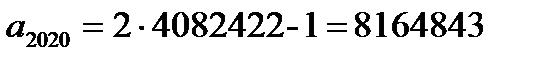 .
.
Ответ: 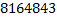
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|