
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
ПРАКТИЧЕСКОЕ ЗАНЯТИЕ №1. МАТРИЦЫ. ОПЕРАЦИИ НАД МАТРИЦАМИ.
ПРАКТИЧЕСКОЕ ЗАНЯТИЕ №1
МАТРИЦЫ. ОПЕРАЦИИ НАД МАТРИЦАМИ.
1.Вычислить произведение матриц:
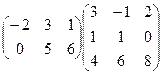 .
.
Решение. Первая матрица имеет размеры 2´3, а вторая размеры 3´3, поэтому произведение существует. В результате умножения получится матрица С = (cij) размеров 2´3. Вычислим ее элементы.
с11 = (-2)×3 + 3×1 + 1×4 = 1, с12 = (-2)×(-1) + 3×1 + 1×6 = 11,
с13 = (-2)×2+3×0+1×8 = 4, с21 = 0×3 + 5×1 + 6×4 = 29,
с22 = 0×(-1) + 5×1 + 6×6 = 41, с23 = 0×2+5×0+6×8 = 48.
Ответ: 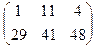 .
.
2.Вычислить произведение матриц:
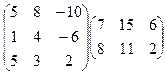 .
.
Решение. Первая матрица имеет размеры 3´3, а вторая размеры 2´3. Число столбцов в первой матрице (3) не совпадает с числом строк во второй матрице (2), поэтому произведение не существует,
Ответ: произведение не существует.
3.Вычислить произведение матриц:
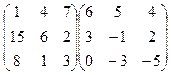 .
.
Ответ: 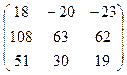 .
.
4.Вычислить произведение матриц:
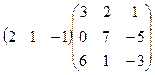 .
.
5.Вычислить произведение матриц:
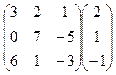 .
.
6.Вычислить произведение матриц:
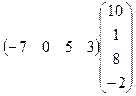 .
.
7.Вычислить произведение матриц:
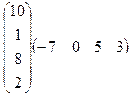 .
.
8.Вычислить произведение матриц:
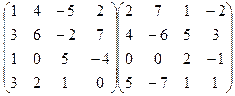 .
.
9.Вычислить степень матрицы:
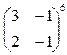 .
.
10. Вычислить степень матрицы:
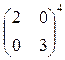 .
.
11. Вычислить значение многочлена f(x) = 2x2 + x - 3 от матрицы 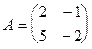 .
.
Указание. f(А) = 2А2 + А - 3Е, где Е – единичная матрица размеров 2´2. Далее использовать определения операций умножения матриц, умножения матрицы на число и сложения матриц.
Ответ: 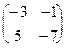 .
.
12. Вычислить значение многочлена f(x) = x3 - x2 + x + 2 от матрицы
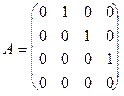 .
.
Ответ: 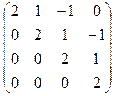 .
.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|