Контакты

Случайная статья

Практическая работа. Координаты и векторы. Основные понятия.. Задание

Стр 1 из 2Следующая ⇒

Практическая работа

Координаты и векторы

Цель работы: закрепить умения выполнять действия над векторами

Основные понятия.

1 Вектором называется отрезок, у которого указано, какой из концов является началом, а какой – концом (направленный отрезок), обозначается 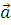, , 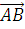где 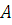- начало вектора, 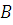- конец.

2 Векторы называются коллинеарными, если они расположены на одной или параллельных прямых.

3 Векторы называются ортогональными, если угол между ними .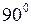

4 Векторы можно складывать ( по правилам треугольника и параллелограмма), можно умножать на число: ; .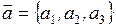

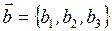
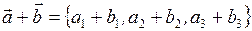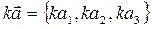5 Необходимое и достаточное условие коллинеарности векторов: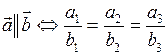

6 Модуль вектора 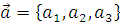равен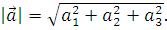

7 Если заданы начало 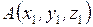и конец 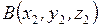вектора 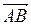, то его координаты и длина находятся следующим образом:

; .

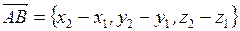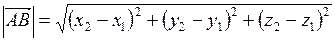8 Скалярным произведением векторов называется число, равное произведению длин этих векторов на косинус угла между ними

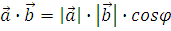
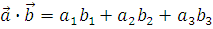
9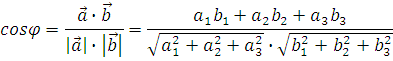

10 Необходимое и достаточное условие ортогональности векторов: .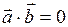

11 Проекция вектора на направление: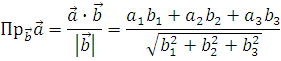

Задание

1 Найти линейную комбинацию векторов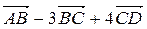

2 Найти длины векторов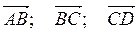

3 Найти косинусы углов между векторами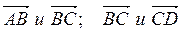

4 Найти Найти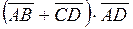

5 Найти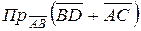

6 Выяснить, коллинеарны ли векторы 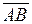и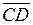

7 Выяснить, ортогональны ли векторы 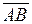и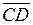

Пример выполнения работы:

Исходные данные:

Даны точки .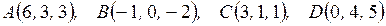

Задание 1 Найти линейную комбинацию векторов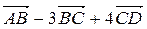

Решение:

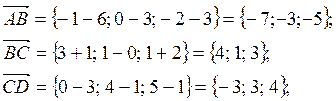
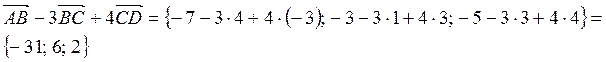
Задание 2 Найти длины векторов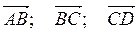

Решение:

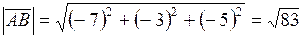
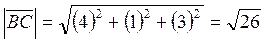
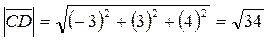
Задание 3 Найти косинусы углов между векторами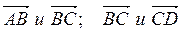

Решение:

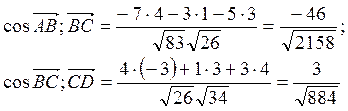
Задание 4Найти Найти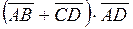

Решение:

Даны точки .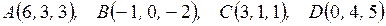

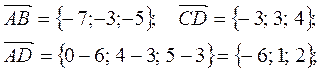
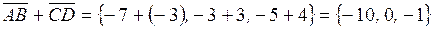
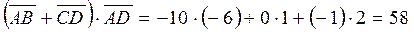
Задание 5Найти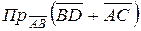

Решение:

,

, ,

.

.

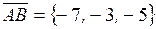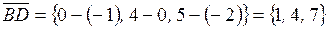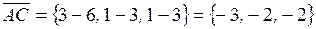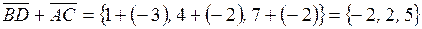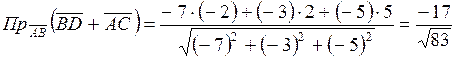Задание 6Выяснить, коллинеарны ли векторы 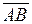и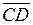

Решение:

,

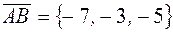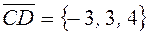
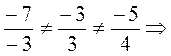векторы не являются коллинеарными.

12 Следующая ⇒

© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.