Федеральное государственное бюджетное образовательное учреждение


МИНОБРНАУКИ РОССИИ
Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования "МИРЭА - Российский технологический университет" РТУ МИРЭА
	Институт информационных технологий (ИТ)
	Кафедра промышленной информатики

ОТЧЕТ ПО ПРАКТИЧЕСКОЙ РАБОТЕ
по дисциплине
«Теория конечных автоматов»

Выполнил студент группы
Принял старший преподаватель	.

работы выполнены	«__»_______202__ г.	_______

«Зачтено»	«__»_______202__ г.	_______

Москва 2020

Содержание

1. Практическая работа №43

1.1. Постановка задачи3

1.2. Задание №13

1.3. Задание №24

1.4. Задание №35

1.5. Задание №46

1.6. Задание №57

1.7. Выводы8

1.8. Список информационных источников9

Практическая работа №2

Элементы теории графов.

Постановка задачи.

Изучить основные элементы теории графов посредством восстановления таблицы смежности по заданному графу и восстановлению графа по заданной таблице смежности.

Вариант 3.

Граф:

Матрица смежности:

	x1	x2	x3	x4	x5	x6
x1
x2
x3
x4
x5
x6

Матрица инцидентности:

	r1	r2	r3	r4	r5	r6	r7
x1
x2
x3
x4
x5
x6

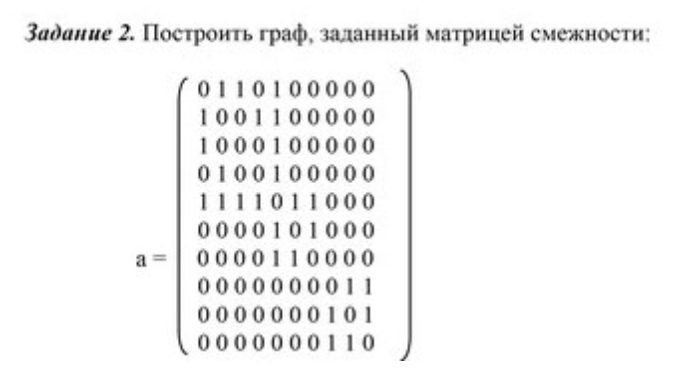
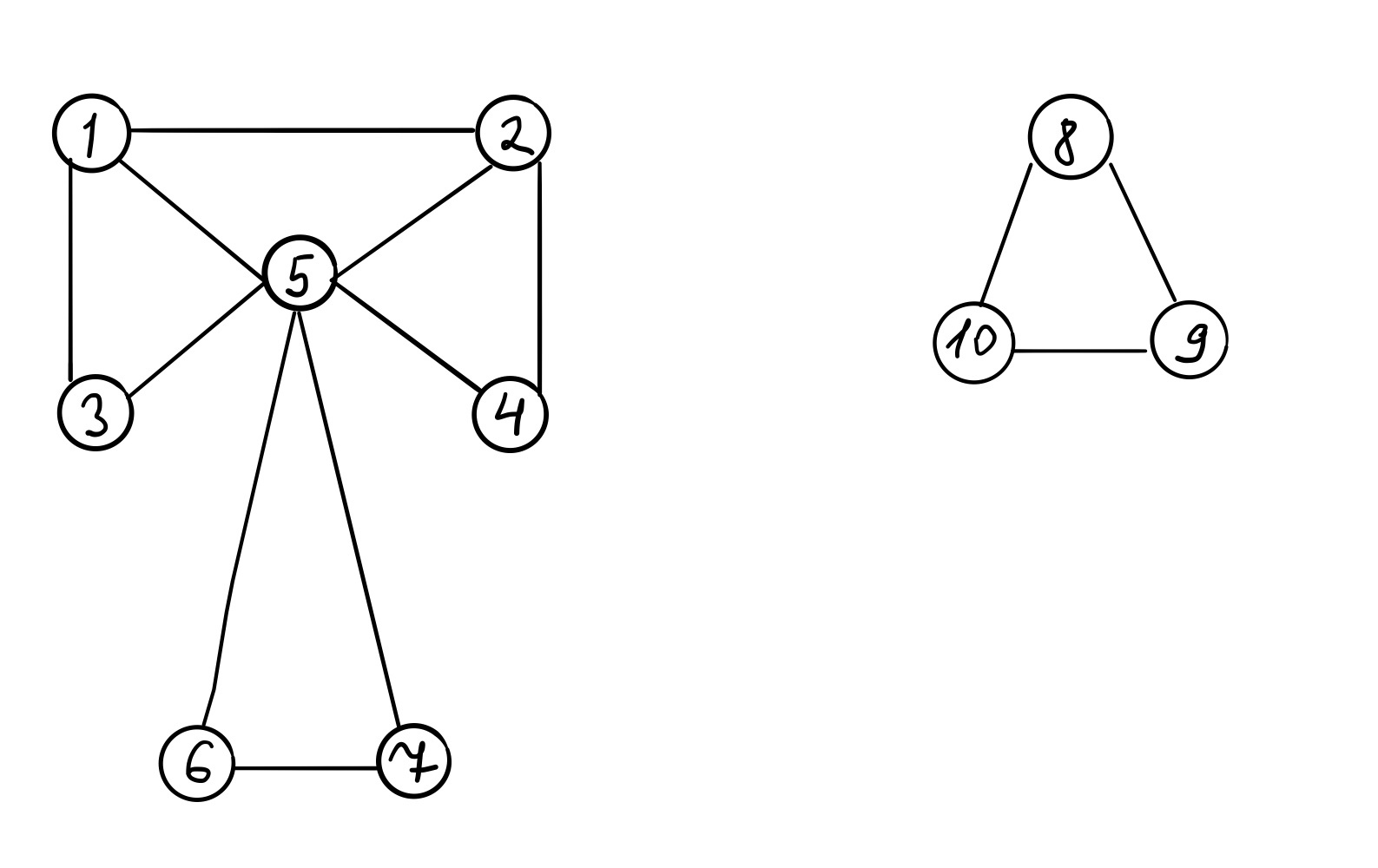
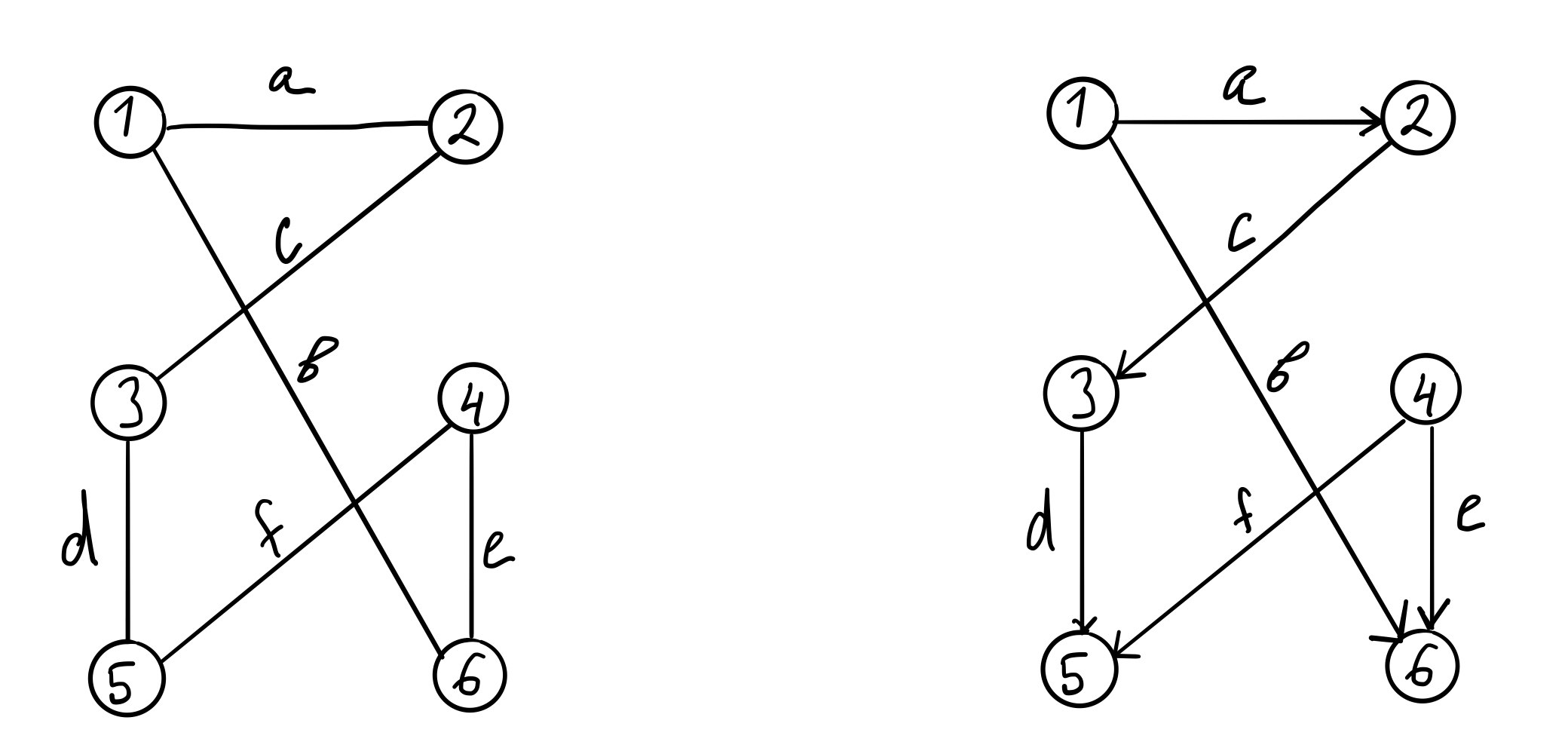
Неориентированный граф (1) Ориентированный граф (2)

a	b	c	d	e	f

Матрица смежности Матрица инцидентности

a	b	c	d	e	f
-1	-1
		-1
			-1
				-1	-1

Матрица смежности Матрица инцидентности

Количество вершин: 8;
Число рёбер: 12;

Степень 3, 4, 6, 8 = 4;
Степень 1, 2, 5, 7 = 2;

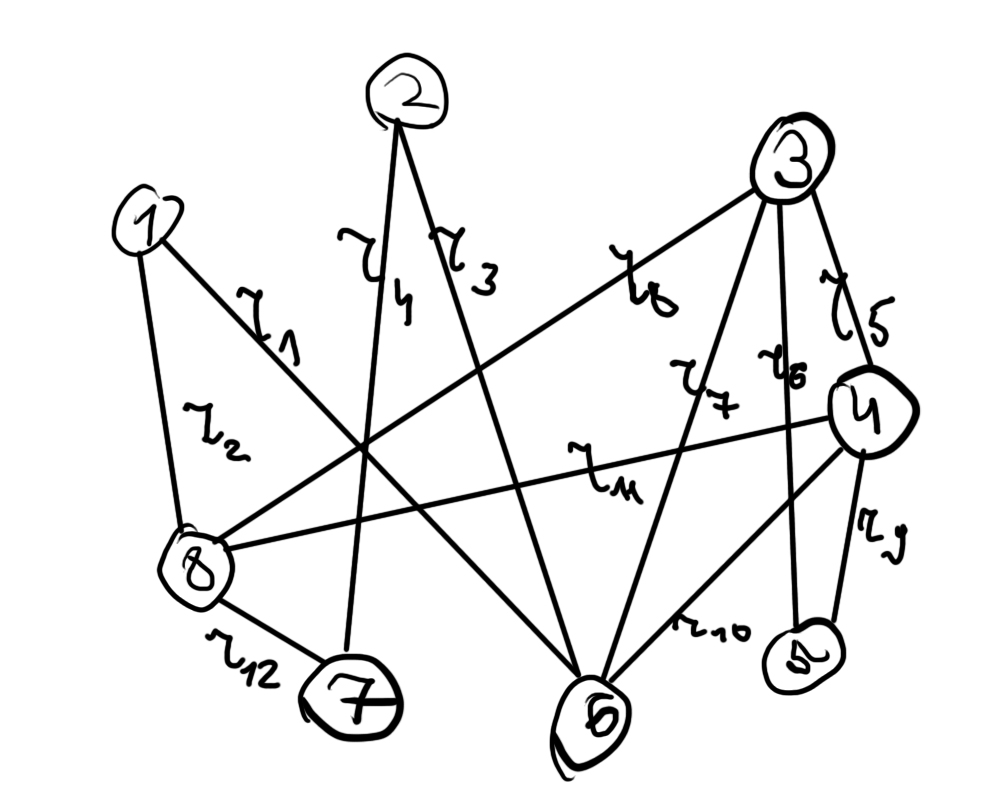
Матрица смежности Матрица инцидентности


-1	-1
		-1	-1
				-1	-1	-1	-1
								-1	-1	-1


											-1

Матрица смежности Матрица инцидентности

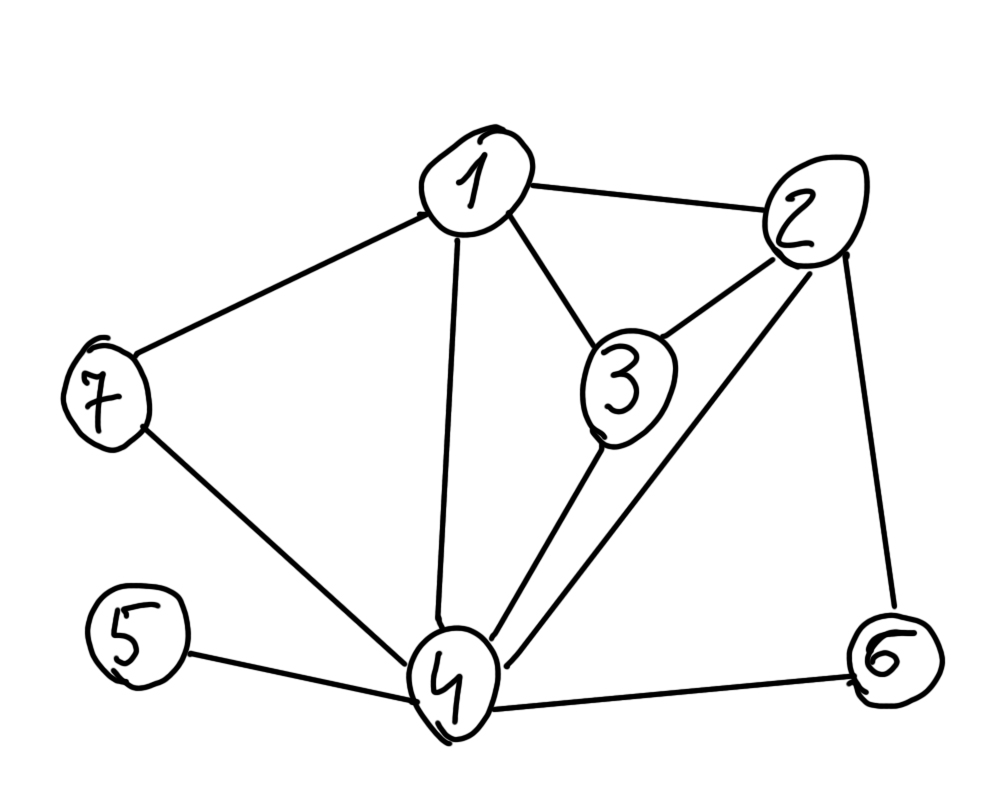
Построить плоское изображение графа возможно

Выводы:

Мы изучили способы построения графов, матриц смежности и инцидентности, преобразовывать неориентированный граф в орграф и наоборот.

Список информационных источников

1. Дистель Р. Теория графов Пер. с англ. - Новосибирск: Издательство института
математики, 2002.
2. Белов В. В., Воробьев Е. М., Шаталов В. Е. Теория графов. — М.: Высш. школа,
1976.
3. Харари Ф. Теория графов. — М.: Мир, 1973. (Изд. 3, М.: КомКнига, 2006. — 296
с.)
4. Татт У. Теория графов. Пер. с англ. М.: Мир, 1988. 424 с