
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Двойственная ЗЛП
Двойственная ЗЛП
Для каждой ЗЛП по определённым правилам можно составить так называемую двойственную задачу.
Чтобы построить двойственную задачи необходимо соблюдать следующими правилами:
1) Если прямая задача решается на максимум, то двойственная — на минимум, и наоборот.
2) В задаче на максимум ограничения-неравенства имеют смысл ≤, а в задаче минимизации - смысл ≥.
3) Каждому ограничению прямой задачи соответствует переменная двойственной задачи, и наоборот, каждому ограничению двойственной задачи соответствует переменная прямой задачи.
4) Матрица коэффициентов при неизвестных в системе ограничений двойственной задачи получается из матрицы коэффициентов при неизвестных в системе ограничений исходной задачи, путем транспонирования.
5) Свободные члены системы ограничений прямой задачи являются коэффициентами при соответствующих переменных целевой функции двойственной задачи, и наоборот.
Экономическое обоснование двойственной задачи:
Прямая задача. Максимизировать функцию
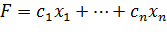
При ограничениях:

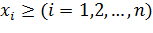
Двойственная задача. Минимизировать функцию
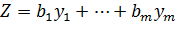
При ограничениях:
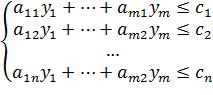
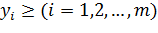
В этих задачах, аявляется расходом сырья определённого вида на производство одного вида продукции, b запасы сырья определённого вида, c - прибыль от реализации единицы продукции определённого вида. В прямой задаче x- количество единиц выпускаемой продукции определённого вида. А в двойственной задаче b - цены сырья соответствующего вида. А целевая функция z - общие затраты на приобретение сырья, которые требуется минимизировать.
Обе задачи имеют самостоятельное значение. К каждой из задач можно применить симплекс метод и получить ответ.
Имеется две теоремы о двойственной задаче. Рассмотрим их ниже:
1) Для взаимно двойственных задач имеется один из следующих взаимоисключающих случаев, относящихся к поиску оптимального решения:
a) Если взаимно двойственные задачи имеет оптимальное решение, то значение ц.ф. на этих оптимальных решениях совпадают.
b) Если область допустимых решений (ОДР) прямой ЗЛП 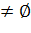 и
и 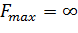 , то ОДР двойственной ЗЛП
, то ОДР двойственной ЗЛП 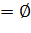
c) Если область допустимых решений двойственной ЗЛП 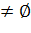 и
и 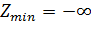 , то ОДР прямой ЗЛП
, то ОДР прямой ЗЛП 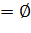
d) Обе задачи имеют ОДР 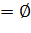 , т.е. не имеют решений
, т.е. не имеют решений
e) Если одна задача имеет бесконечное множество решений, то решение другой вырожденное.
2) Между переменными взаимно двойственных задач существует взаимообратная однозначное соответствие.
a) Основные переменные одной задачи являются добавочными другой.
b) Все положительные компоненты в решении прямой задачи будут соответствовать нулевым компонентам в оптимальном решении двойственной задачи.


c) Все остальные компоненты оптимального решения двойственной задачи равны абсолютному (по модулю) значению коэффициентов при соответствующим переменным ц.ф. прямой задачи, выраженные через неосновные переменные.
Теперь попробуем составить двойственную задачу от нашей первоначальной ЗЛП, а потом определим ее оптимальное решение.
Прямая задача:
Целевая функция: 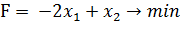
Система ограничений: 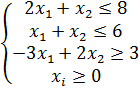
Запишем целевую функцию и значение базисного вектора на последней итерации симплекс-метода систем. Эти данные являются решением прямой ЗЛП.
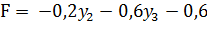
Вектор оптимального решения:
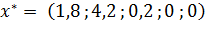
Далее запишем двойственную ЗЛП по правилам, которые были указаны выше.
Целевая функция: 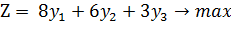
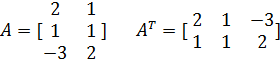
Система ограничений: 

Схема соответствия неизвестных
На основе оптимального решения прямой задачи запишем теперь оптимальное решение для двойственной задачи. Если посмотреть на схему соответствия неизвестных, приведенной выше, то здесь видно, что для всех переменных кроме 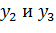 значение координаты в векторе оптимального решения будут равны нулю (см. вторую теорему двойственности). А дабы узнать координаты для
значение координаты в векторе оптимального решения будут равны нулю (см. вторую теорему двойственности). А дабы узнать координаты для 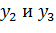 , посмотрим на ц.ф. прямой задачи в последней итерации. Возьмем оттуда коэффициенты при соответствующих неизвестных по абсолютному значению и запишем их в вектор оптимального решения двойственной задачи.
, посмотрим на ц.ф. прямой задачи в последней итерации. Возьмем оттуда коэффициенты при соответствующих неизвестных по абсолютному значению и запишем их в вектор оптимального решения двойственной задачи.
Вектор оптимального решения двойственной задачи:
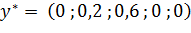
Так как значение прямой целевой функции в точке оптимума соответствует: 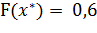 , то значение двойственной функции в своей точке оптимума также соответствует:
, то значение двойственной функции в своей точке оптимума также соответствует: 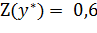
Ответ: 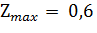 при
при 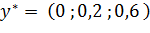
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|