Критерии оценивания

Дата: 11 ноября 2020 г.

Номер группы: 121

Дисциплина: ОДУ 11. Информатика

Тема занятия: Использование деревьев

План изучения нового материала:

Видеоурок: Структуры данных деревья, сети, графы, таблицы(https://www.youtube.com/watch?v=yvwQYXWmvzo)

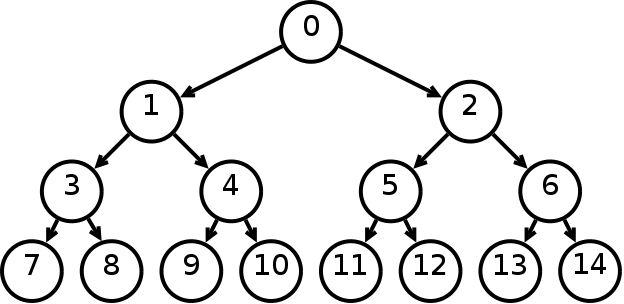
Бинарное дерево — это иерархическая структура данных, в которой каждый узел имеет значение (оно же является в данном случае и ключом) и ссылки на левого и правого потомка. Узел, находящийся на самом верхнем уровне (не являющийся чьим либо потомком) называется корнем. Узлы, не имеющие потомков (оба потомка которых равны NULL) называются листьями.

Рис. 1 Бинарное дерево

Бинарное дерево поиска — это бинарное дерево, обладающее дополнительными свойствами: значение левого потомка меньше значения родителя, а значение правого потомка больше значения родителя для каждого узла дерева. То есть, данные в бинарном дереве поиска хранятся в отсортированном виде. При каждой операции вставки нового или удаления существующего узла отсортированный порядок дерева сохраняется. При поиске элемента сравнивается искомое значение с корнем. Если искомое больше корня, то поиск продолжается в правом потомке корня, если меньше, то в левом,если равно, то значение найдено и поиск прекращается.

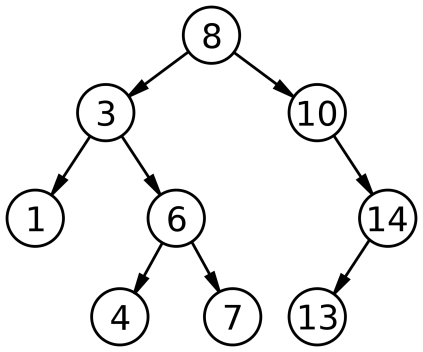Рис. 2 Бинарное дерево поиска

Сбалансированное бинарное дерево поиска — это бинарное дерево поиска с логарифмической высотой. Данное определение скорее идейное, чем строгое. Строгое определение оперирует разницей глубины самого глубокого и самого неглубокого листа (в AVL-деревьях) или отношением глубины самого глубокого и самого неглубокого листа (в красно-черных деревьях). В сбалансированном бинарном дереве поиска операции поиска, вставки и удаления выполняются за логарифмическое время (так как путь к любому листу от корня не более логарифма). В вырожденном случае несбалансированного бинарного дерева поиска, например, когда в пустое дерево вставлялась отсортированная последовательность, дерево превратится в линейный список, и операции поиска, вставки и удаления будут выполняться за линейное время. Поэтому балансировка дерева крайне важна. Технически балансировка осуществляется поворотами частей дерева при вставке нового элемента, если вставка данного элемента нарушила условие сбалансированности.

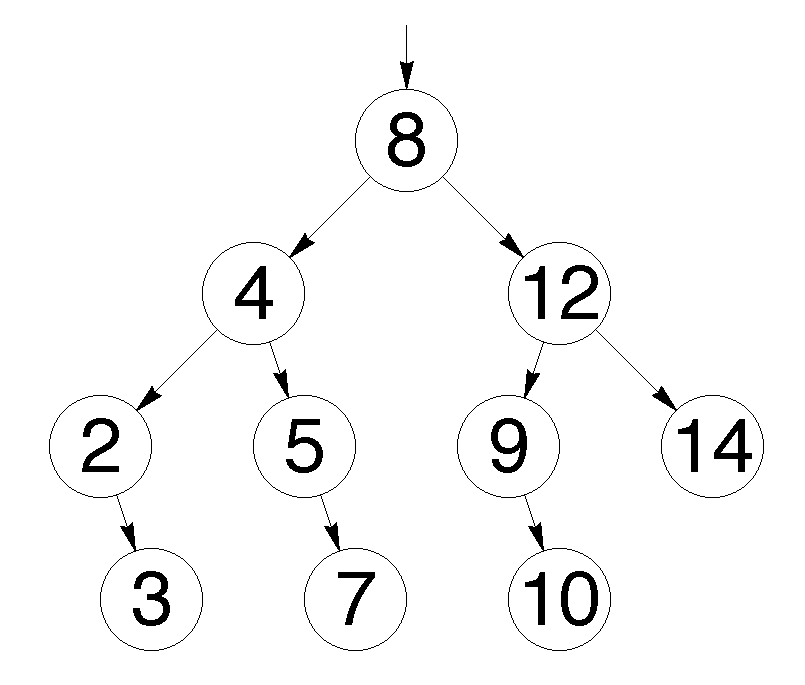Рис. 3 Сбалансированное бинарное дерево поиска

Сбалансированное бинарное дерево поиска применяется, когда необходимо осуществлять быстрый поиск элементов, чередующийся со вставками новых элементов и удалениями существующих. В случае, если набор элементов, хранящийся в структуре данных фиксирован и нет новых вставок и удалений, то массив предпочтительнее. Потому что поиск можно осуществлять алгоритмом бинарного поиска за то же логарифмическое время, но отсутствуют дополнительные издержки по хранению и использованию указателей.

Контрольные вопросы:

1.Бинарное дерево – это?

2. Перечислите свойства бинарного дерева

3. Сбалансированное бинарное дерево поиска – это?.

Критерии оценивания

Вид работы	Оценка
Вид работы
Теоретические ответы	выполнено более 90% работы; обучающийся выделяет главные положения в изученном материале; свободно применяет полученные знания на практике; не допускает ошибок в письменных работах, последние выполняет аккуратно	выполнено не менее 80% работы; обучающийся отвечает без особых затруднений; умеет применять полученные знания на практике; в ответах не допускает серьезных ошибок, в письменных работах делает незначительные ошибки	выполнено не менее 70% работы; обучающийся испытывает затруднения при его самостоятельном воспроизведении; испытывает затруднения при ответах на видоизмененные вопросы; допускает ошибки в письменных работах

3. Учебник

Семакин И.Г. Информатика. Углубленный уровень: учебник для 10 класса: в 2 ч. Ч. 1 / И.Г.семакин, Т.Ю.Шейна, Л.В.Шестакова. – М.:БИНОМ.Лаборатория знаний, 2016. – 184с. : ил. - ISBN 978-5-9963-1811-7.

4. Внеаудиторная самостоятельная работа: Использование деревьев при хранении данных - презентация

5.Адрес почты: Выполненные задания присылать на электронную почту

Галкиной Г.С. - galkinag2020@gmail.com

Догадаевой Т.Ю. – dogadaevat@mail.ru