Раздел 3. Прямые и плоскости в пространстве

26.11.20 г.

Раздел 3. Прямые и плоскости в пространстве

Тема 3.3. Геометрические преобразования

Геометрические преобразования пространства: параллельный перенос,

симметрия относительно плоскости

Параллельным переносом в пространстве называется такое преобразование, при котором произвольная точка (х; у; z) фигуры переходит в точку (х + а; y + b; z + c), где числа а, b, с одни и те же для всех точек (х; у; z). Параллельный перенос в пространстве задается формулами:

х' = х + а, у' = у + b, z' = z + c,

Параллельный перенос в пространстве обладает следующими свойствами:

1. Параллельный перенос есть движение.

2. При параллельном переносе точки смещаются по параллельным прямым на одно и то же расстояние.

3. При параллельном переносе каждая прямая переходит в параллельную ей прямую или в себя.

4. Каковы бы ни были точки A и A`, существует единственный параллельный перенос, при котором точка A переходит в точку A`.

5. При параллельном переносе в пространстве каждая плоскость переходит либо в себя, либо в параллельную ей плоскость.

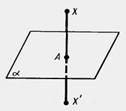
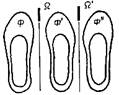
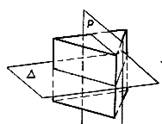
Симметрия относительно плоскости– это такое свойство геометрической фигуры, когда любой точке, расположенной по одну сторону плоскости, всегда будет соответствовать точка, расположенная по другую сторону плоскости, а отрезки, соединяющие эти точки, будут перпендикулярны плоскости симметрии и делятся ею пополам.