Математическое ожидание дискретной случайной величины

Статистика 26.11.2020 г.

(дисциплина)

Группа :_1012,1013,1011,1010,1009

Преподаватель: Лобасова Т.А.

Тема: Математическое ожидание дискретной случайной величины, свойства.

ЛЕКЦИОНННЫЙ МАТЕРИАЛ

Математическое ожидание дискретной случайной величины

Определение: Математическим ожиданием дискретной случайной величины называется сумма произведений всех возможных её значений на вероятности этих значений:

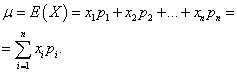
Пример . Закон распределения измерений задан таблицей. Найти М(Х)

Число измеренных экземпляров	Вероятность
	0,20
	0,40
	0,25
	0,10
	0,05

Решение.

М(Х) = 50*0,2+100*0,4+200*0,25+300*0,1+400*0,05=10+40+50+30+20=150

В следующей таблице обобщены ожидаемые значения случайной величины - прибыли:

Прибыльxi	Вероятностьpi
	0,25
	0,45
	0,3

Таким образом, получаем математическое ожидание прибыли:

М(Х) = 125*0,25+50*0,45+100*0,3=31,25+22,5+30=83,75

Свойства математического ожидания

Свойство 1.Математическое ожидание постоянной величины равно этой постоянной:

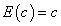
Свойство 2.Постоянный множитель можно выносить за знак математического ожидания:

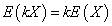
Свойство 3.Математическое ожидание суммы (разности) случайных величин равно сумме (разности) их математических ожиданий:

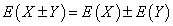
Свойство 4.Математическое ожидание произведения случайных величин равно произведению их математических ожиданий:

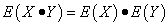
Свойство 5.Если все значения случайной величины X уменьшить (увеличить) на одно и то же число С, то её математическое ожидание уменьшится (увеличится) на то же число:

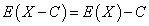
Примеры: 1)Найти М(4х+17), если М(Х)=3

Решение: М(4х+17)= М(4х)+ М(17)=4М(х)+17=4*3+17=12+17=29

2)Найти М(2,5х-3,5), если М(Х)=1,5

Решение:

М(2,5х-3,5)= М(2,5х)- М(3,5)=2,5М(х) - 3,5=2,5*1,5-3,5=3,75-3,5=0,25

Литература:

1. Мхитарян В.С., Дубова Т.А., Минашкин В.Г. Статистика: учебник - М.: ОИЦ «Академия», 2019.

2. Салин В.Н., Чурилова Э.Ю., Шпаковская Е.П. Статистика: учебное пособие – М. КноРус, 2018.

3. Шмойлова Р.А. Практикум по теории статистики: учебное пособие – М.Финансы и статистика, 2017

Дополнительные источники:

Журнал «Вопросы статистики»
Статистические ежегодники

Интернет источники:

Портал статистических данных - "Статистика. ru": [Электронный ресурс] - Режим доступа: http://statistika.ru/
Федеральная служба государственной статистики [Электронный ресурс]. – Режим доступа: http://www.gks.ru/