урок в Zoom. Тема урока. Линейная функция и её график. (3 модуля). О: Уравнение видаax+by+c=0, гдеa, b, c— числа (коэффициенты), называется линейным уравнением с двумя переменнымиxиy.. модуль (теоретический). Линейная функция и её график».

2,3 урок в Zoom

Тема урока. Линейная функция и её график. (3 модуля)

О: Уравнение видаax+by+c=0, гдеa, b, c— числа (коэффициенты), называется линейным уравнением с двумя переменнымиxиy.

Применяя эту формулу, зная конкретное значение x, можно вычислить соответствующее значение y.

Пусть y=0,5x−2.

Тогда:

если x=0, то y=−2;

если x=2, то y=−1;

если x=4, то y=0 и т. д.

Обычно эти результаты оформляют в виде таблицы:

x
y	−2	−1

x — независимая переменная (или аргумент),

y — зависимая переменная.

О:Линейная функция — это функция, которую можно задать формулой y=kx+m, где x — независимая переменная, k и m — некоторые числа.

1 модуль (теоретический)

1. ЗАПИШИ В ТЕТРАДЬ ЧИСЛО И ТЕМУ УРОКА!

«Линейная функция и её график».

ТЕОРИЯ

ЗАКРЕПЛЕНИЕ (карта усвоения материала)

2. Прослушайте теоретический материал по теме раздела!

3. Разбери!

1. ZOOM (время урока) 2. Цифровая школа Оренбуржья http://77.41.182.159/theme.php?id=1605 ЗАРЯДКА ДЛЯ ГЛАЗ!!! https://pplisey1.my1.ru/_nw/9/82779615.jpg

Пример:

построить график линейной функции:

a) y=−2x+1, x∈[−3;2] b) y=−2x+1, x∈(−3;2).

y=−2x+1- линейная функция, графиком является прямая.

Составим таблицу значений функции:

x	−3
y		−3

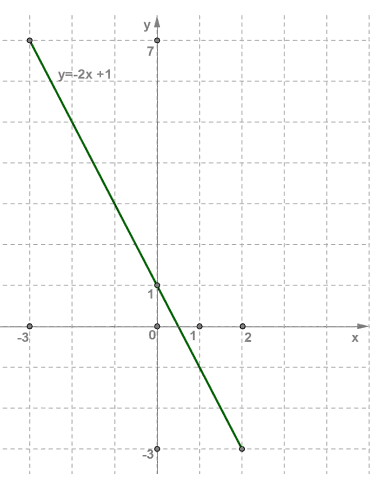
Построим на координатной плоскости xOy точки (−3;7) и (2;−3) и

проведём через них прямую.

Далее выделим отрезок, соединяющий построенные точки.

Этот отрезок и есть график линейной функции y=−2x+1, x∈[−3;2].

Точки (−3; 7) и (2; −3) на рисунке отмечены тёмными кружочками.

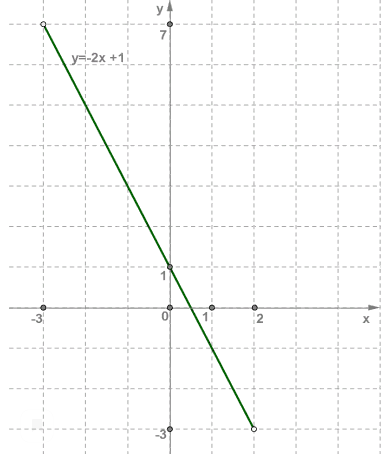
b) Во втором случае функция та же, только значения x=−3 и x=2 не рассматриваются, так как они не принадлежат интервалу (−3;2).

Поэтому точки (−3; 7) и (2; −3) на рисунке отмечены светлыми кружочкам.

Рассматривая график линейной функции на отрезке, можно назвать наибольшее и наименьшее значения линейной функции.

В случае

a) y=−2x+1, x∈[−3;2] имеем, что yнаиб =7 и yнаим =−3;

b) y=−2x+1, x∈(−3;2) имеем, что ни наибольшего, ни наименьшего значений линейной функции нет, так как оба конца отрезка, в которых как раз и достигались наибольшее и наименьшее значения, исключены из рассмотрения.

В ходе построения графиков линейных функций можно как бы «подниматься в горку» или «спускаться с горки», т. е. линейная функция или возрастает, или убывает.

12 Следующая ⇒