Решение показательных уравнений.

Практическая работа

Решение показательных уравнений.

Цель: закрепление и систематизация знаний о методах решения показательных уравнений и выработку самостоятельно решать показательные уравнения.

Задания для самостоятельного решения

Задание 1. Решите уравнение методом уравнивания оснований.

А)3^х=27; Б) 7^х+3=343; В) 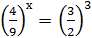; Г) .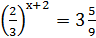

Задание 2. Решите уравнение методом вынесения общего множителя за скобки.

А)7^х+1- 5·7^х = 98; Б) 7·3^{х +3} + 3^{х +2}= 22·

Задание 3. Решите уравнение методом введения новой переменной.

А)4^х - 17·2^х+16= 0; Б) ·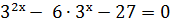

Краткие теоретические основы

Определение: Показательным уравнением называется уравнение, в котором переменная содержится в показателе степени.

Простейшее показательное уравнение – это уравнение вида:

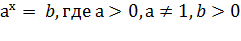
Уравнение a^x = b не имеет корней, если b<0.

Методы решения показательных уравнений:

1. Уравнивание оснований.

Алгоритм метода:

1. Уединить слагаемое, содержащее переменную.

2. Привести степени к одному основанию.

3. Приравнять показатели.

4. Решить полученное уравнение.

5. Записать ответ.

Пример 1: 3^х - 27 = 0; 3^х = 27; (1 шаг) 3^х = 3³; (2 шаг) х = 3 (3 шаг) Ответ: x = 3. (5 шаг)

Пример 2: 2^х-4 - 16 = 0; 2^х-4 = 16; (1 шаг) 2^х-4 =2⁴; (2 шаг) х-4=4 (3 шаг) х=4+4 (4 шаг) х=8 Ответ: x = 8. (5 шаг)

2. Вынесение общего множителя за скобки.

Алгоритм метода:

1. Применяя свойства степени 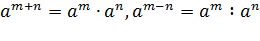, выделить множители, в которых переменная содержится в показатели степени.

2. Вынести общий множитель за скобки.

3. Подсчитать значение выражения в скобке.

4. Привести уравнение к виду .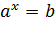

5. Решить полученное уравнение методом уравнивание показателей.

Пример 3:

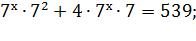( 1 шаг )

(2 шаг)

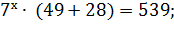(3 шаг)

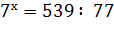; (4 шаг)

; (5 шаг)

х=1.

Ответ: 1

3. Введение новой переменной

Алгоритм метода:

1. Избавиться от числовых слагаемых в показателях степеней (если они есть и не совпадают).

2. Приведите степени к одному основанию.

3. Сделать замену переменной. Обязательно вести условие, что новая переменная больше нуля .

4. Решить полученное квадратное уравнение. Если в решении квадратного уравнения получились отрицательные корни, то необходимо указать , что он не удовлетворяет условию пункта 3.

5. Сделать обратную замену, и решить простейшие показательные уравнения.

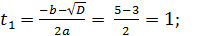
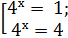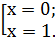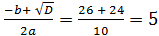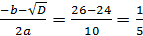
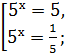Пример 4: Примечание: в данном уравнении 1 и 2 шаги отсутствует. 4^2x- 5·4^x + 4 = 0; 4^x = t, t>0 ; (3 шаг) t²-5·t + 4 = 0; (4 шаг) D = 25-16 = 9; (5 шаг ) Ответ: 0; 1.	Пример 5: В данном примере отсутствует только шаг 2. 5^2x+1 - 26∙5^x +5 = 0; 5^2x ⋅5¹– 26 ⋅ 5^x +5 = 0; (1 шаг) 5^x = t, t > 0; (3 шаг) 5t² - 26t + 5 = 0; (4 шаг) D=676 – 100 = 576; t₁= t₂= (5 шаг) Ответ: -1; 1.
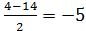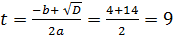Пример 6: 9^x - 4 · 3^x – 45 = 0 ; т.к. 9^x = (3²)^x= 3²^x = (3^x)²; 3^x = t, t > 0 ; t² – 4t – 45 = 0; D = 16 – 4 ⋅ (- 45)=196; t₁ = не удовлетворяет условию t >0. ; 3^x = 9; 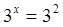; х = 2. Ответ: 2