
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Конспект урока математики . Форма работы: индивидуальная, дистанционное обучение.. Организационный этап. Мотивационный модуль
Преподаватель Липницкая В.Н. lipnickaya.1956@mail.ru
Конспект урока математики
Дата 20.11.2020г
Курс 2
Группа 3
Тема урока: «Определенный интеграл. Площадь криволинейной трапеции.»
Урок № 26
Форма работы: индивидуальная, дистанционное обучение.
Тип урока: урок изучения нового материала.
Цель урока:формировать систему знаний и умений, связанных с понятием определенный интеграл.
Изучаемая литература:1. Башмаков М.И., учебник для 11 класса (базовый уровень) 4 издание, издательский центр» Академия» 2018г
Математика : алгебра и начала математического анализа, геометрия. Алгебра и начала математического анализа.
10-11 классы: учеб.для общеобразоват.организаций: базовый и углубл.уровени./Ш.А.Алимов, Ю.М.Колягин, М.В.Ткачева и др.- 5 изд.- М.: Просвещение , 2018г
Интернет-ресурсы: Математика в открытом колледже http://www.mathematics.ru
Ход занятия :
1. Организационный этап. Мотивационный модуль
Ребята, сегодня, вы рассмотрите материал, связанный с определенным интегралом, выполните задания на нахождение площади криволинейной трапеции.
1) Нахождение определенного интеграла
2) Нахождение площади криволинейной трапеции с помощью формулы Ньютона – Лейбница
3) Решение задач, с помощью формулы Ньютона – Лейбница
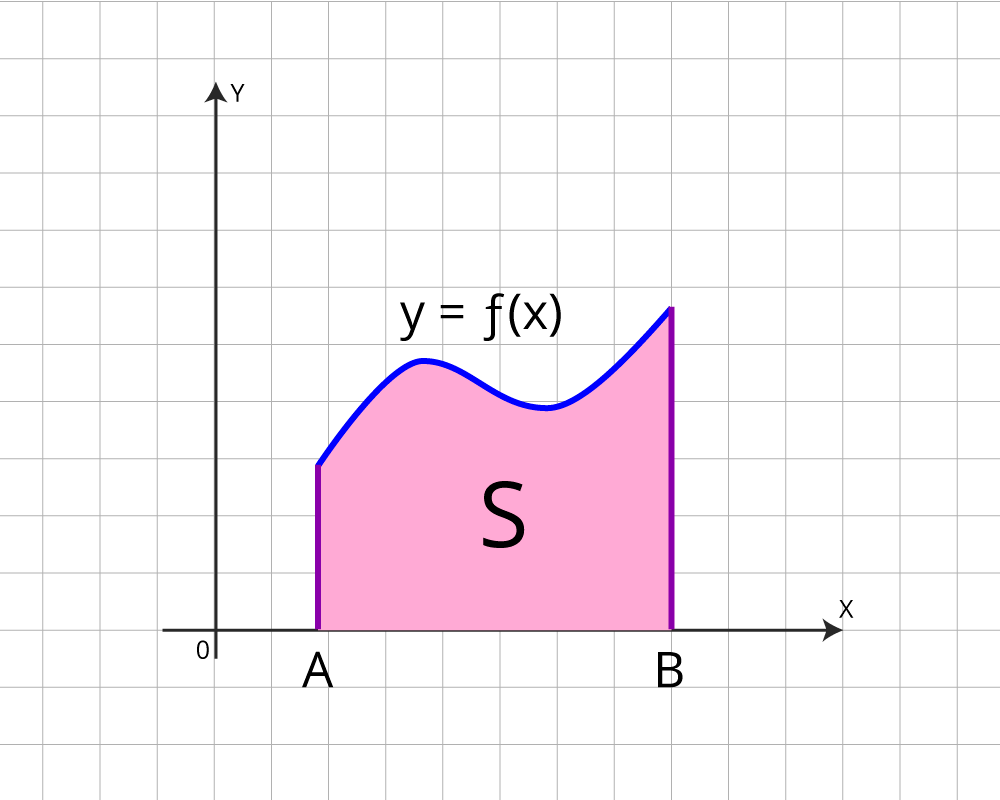
Криволинейной трапецией называется фигура, ограниченная графиком непрерывной и не меняющей на отрезке [а;b] знака функции f(х), прямыми х=а, x=b и отрезком [а;b].
Отрезок [a;b] называют основанием этой криволинейной трапеции
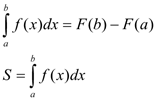
формула Ньютона – Лейбница
Примеры и разбор решения заданий тренировочного модуля
№1.Найти площадь криволинейной трапеции, изображенной на рисунке
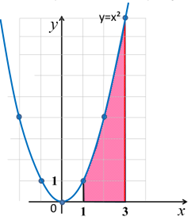
Решение
Для вычисления площади криволинейной трапеции воспользуемся формулой Ньютона – Лейбница.
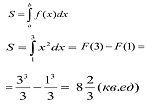
Ответ: 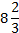
№2. Вычислить определенный интеграл:
Решение: Воспользуемся формулой Ньютона-Лейбница.
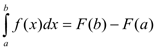
Сначала находим первообразную функцию F(x) . Далее подставляем значение верхнего предела в первообразную функцию: F(b) .
Затем подставляем значение нижнего предела в первообразную функцию: F(а).
Рассчитываем разность F(b) - F(а), это и будет ответ.
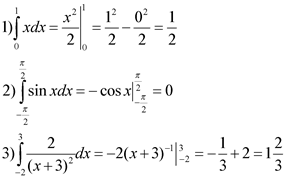
№3. Найти площадь криволинейной трапеции (х-1)2, ограниченной линиями х=2 и х=1, осью 0х
Решение:
Воспользуемся формулой Ньютона-Лейбница.
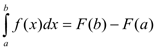
Сначала находим первообразную функцию F(x). Далее подставляем значение верхнего предела в первообразную функцию: F(b) .
Затем подставляем значение нижнего предела в первообразную функцию: F(а).
Рассчитываем разность F(b) - F(а), это и будет ответ.
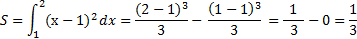
Домашнее задание: составить конспект по теме урока
Контрольное задание Вычислить определенный интеграл
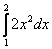
Конспект и выполненные задания отправить личным сообщением в ВК
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|