Ответы на контрольные вопросы

Ответы на контрольные вопросы

1. В чем заключается нормирование метрологических характеристик средств измерений.

Нормирование метрологических характеристик – это регламентирование пределов отклонений значений реальных метрологических характеристик средств измерений от их номинальных значений. Главная цель нормирования метрологических характеристик – это обеспечение их взаимозаменяемости и единства измерений.

Осуществляется двумя способами:

1. Путем установления номинальной метрологической характеристики средств измерений данного типа.

2. Путем указания пределов, в которых должно находиться значение нормируемой метрологической характеристики.

2. Назовите виды средств измерений.

К основным видам средств измерений относятся следующие:

· эталон;

· мера;

· измерительный преобразователь;

· измерительный прибор;

· измерительная установка;

· измерительная система.

3. Назовите виды погрешностей средств измерений.

Погрешность средства измерений – разность между показанием средства измерений и истинным (действительным) значением измеряемой физической величины.

Систематическая погрешность средства измерений – составляющая погрешности средства измерений, принимаемая за постоянную или закономерную изменяющуюся.

Случайная погрешность средства измерений – составляющая погрешности средства измерений, изменяющаяся случайным образом.

Абсолютная погрешность средства измерений – погрешность средства измерений, выраженная в единицах измеряемой физической величины.

Относительная погрешность средства измерений – погрешность средства измерений, выраженная отношением абсолютной погрешности средства измерений к результату измерений или к действительному значению измеренной физической величины.

Приведенная погрешность средства измерений – относительная погрешность, выраженная отношением абсолютной погрешности средства измерений к условно принятому значению величины, постоянному во всем диапазоне измерений или в части диапазона.

Основная погрешность средства измерений – погрешность средства измерений, применяемого в нормальных условиях.

Дополнительная погрешность средства измерений – составляющая погрешности средства измерений, возникающая дополнительно к основной погрешности вследствие отклонения какой-либо из влияющих величин от нормального ее значения или вследствие ее выхода за пределы нормальной области значений.

Статическая погрешность средства измерений – погрешность средства измерений, применяемого при измерении физической величины, принимаемой за неизменную.

Динамическая погрешность средства измерений – погрешность средства измерений, возникающая при измерении изменяющейся (в процессе измерений) физической величины.

Погрешность меры – разность между номинальным значением меры и действительным значением воспроизводимой ею величины.

4. Приведите виды классов точности средств измерений.

Точность средства измерений – характеристика качества средства измерений, отражающая близость его погрешности к нулю.
Примечание. Считается, что чем меньше погрешность, тем точнее средство измерений.

Класс точности средств измерений – обобщенная характеристика данного типа средств измерений, как правило, отражающая уровень их точности, выражаемая пределами допускаемых основной и дополнительных погрешностей, а также другими характеристиками, влияющими на точность.

Средства измерений выпускаются на следующие классы точности: 0,01; 0,015; 0,02; 0,025; 0,04; 0,05; 0,1; 0,15; 0,2; 0,25; 0,4; 0,5; 0,6; 1,0; 1,5; 2,0; 2,5; 4,0; 5,0; 6,0. Класс точности средств измерении характеризует их свойства в отношении точности, но не является непосредственным показателем точности измерений, выполняемых с помощью этих средств (под точностью средств измерений понимается качество измерений, отражающее близость нулю их погрешностей). На циферблаты, шкалы, щитки, корпуса средств измерений всегда наносят условные обозначения класса точности, включающие числа и прописные буквы латинского алфавита.

5. Что такое измерительная система и измерительные каналы.

Измерительные системы обладают основными признаками средств измерений (СИ) и являются их специфической разновидностью. Основными областями применения собственно измерительных систем являются научные исследования, испытания различных объектов, учетные операции, и др.

Наиболее крупной структурной единицей, для которой могут нормироваться метрологические характеристики (MX), является измерительный канал (ИК): конструктивно или функционально выделяемая часть ИС, выполняющая законченную функцию от восприятия измеряемой величины до получения результата ее измерений, выражаемого числом или соответствующим ему кодом, или до получения аналогового сигнала, один из параметров которого — функция измеряемой величины.

ИК представляет собой последовательное соединение СИ, образующих ИС (некоторые из этих СИ сами могут быть многоканальными, в этом случае следует говорить о последовательном соединении ИК указанных СИ). Такое соединение СИ, предусмотренное алгоритмом функционирования, выполняет законченную функцию от восприятия измеряемой величины до индикации или регистрации результата измерений включительно, или преобразование его в сигнал, удобный для дальнейшего использования вне ИС, для ввода в цифровое или аналоговое вычислительное устройство,

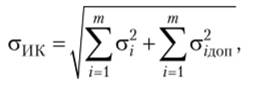входящее в состав ИС, для совместного преобразования с другими величинами, для воздействия на исполнительные механизмы.

6. Какова методика расчета погрешности измерительной системы.

Измерительная система по определению, предназначена для восприятия, переработки и хранения измерительной информации в общем случае разнородных физических величин по различным измерительным каналам (ИК). Поэтому расчет погрешности измерительной системы сводится к оценке погрешностей ее отдельных ИК. Результирующая относительная погрешность ИК будет: где х — текущее значение измеряемой величины; хп — предел данного диапазона измерения канала, при котором относительная погрешность минимальна; δ_И, δ_К — относительные погрешности, вычисленные соответственно в начале и конце диапазона.

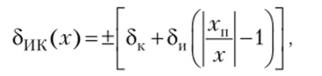Поскольку ИК есть цепь различных воспринимающих, преобразовательных и регистрирующих звеньев, то для определения δ_ИК (х) необходимо прежде всего оценить СКО погрешностей этих т звеньев с.. Тогда результирующая СКО погрешности ИК будет

7. Что такое рабочая зона средств измерения.

Шкала — часть показывающего устройства средства измерений, представляющая собой упорядоченный ряд отметок вместе со связанной с ними нумерацией или техническая отметка на шкале измерительного прибора. Шкалы могут располагаться по окружности, дуге или прямой линии. Показания отсчитываются невооружённым глазом при расстояниях между делениями до 0,7 мм, при меньших — при помощи лупы или микроскопа, для долевой оценки делений применяют дополнительные шкалы — нониусы.

Элементы шкалы:

· Отметка шкалы — знак на шкале (чёрточка, зубец, точка и т.д.), соответствующий некоторому значению физической величины.

· Числовая отметка шкалы — отметка шкалы, у которой проставлено число.

· Нулевая отметка — отметка шкалы, соответствующая нулевому значению измеряемой величины.

· Деление шкалы — промежуток между двумя соседними отметками шкалы.

· Длина деления шкалы — расстояние между осями (или центрами) двух соседних отметок шкалы, измеренное вдоль воображаемой линии, проходящей через середины самых коротких отметок шкалы.

· Цена деления шкалы — разность значений величины, соответствующих двум соседним отметкам шкалы.

· Длина шкалы — длина линии, проходящей через центры всех самых коротких отметок шкалы и ограниченной начальной и конечной отметками. Линия может быть реальной или воображаемой, кривой или прямой.

· Интервал деления шкалы (деление шкалы) — расстояние между осями симметрии двух рядом лежащих штрихов (выражается в линейных или в угловых единицах)

Виды шкал измерений:

· Односторонняя шкала — шкала с нулевой отметкой, расположенной в начале или в конце шкалы

· Двусторонняя шкала — шкала с нулевой отметкой, расположенной между начальной и конечной отметками. Различают симметричные (начальная и конечная отметки соответствуют одинаковым значениям измеряемой величины) и несимметричные двусторонние шкалы (начальной и конечной отметкам соответствуют разные значения).

Свойства шкал:

Начальное значение шкалы — наименьшее значение измеряемой величины, которое может быть отсчитано по шкале средства измерений. Во многих случаях шкала начинается с нулевой отметки, однако могут быть и другие значения — например, у медицинского термометра это 34,3 °C.

Конечное значение шкалы — наибольшее значение измеряемой величины, которое может быть отсчитано по шкале средства измерений.

Характер шкалы — функциональная зависимость a = f(x) между линейным (или угловым) расстоянием a какой-либо отметки от начальной отметки шкалы, выраженным в долях всей длины шкалы, и значением x измеряемой величины, соответствующим этой отметке:

· Равномерная шкала — шкала, отметки на которой нанесены равномерно.

· Неравномерная шкала — шкала, отметки на которой нанесены неравномерно.

· Логарифмическая или гиперболическая шкала — шкала с сужающимися делениями, характеризуемыми тем, что отметка, соответствующая полусумме начального и конечного значений, расположена между 65 и 100 % длины шкалы. Следует заметить, что выражение «логарифмическая шкала» используется и по отношению к другому значению понятия «шкала» Степенная шкала — шкала с расширяющимися или сужающимися делениями, но не подпадающая под определение логарифмической (гиперболической) шкалы.

8. В чем различие метрологических характеристик аналоговых и цифровых средств измерений.

В цифровом приборе непрерывная по размеру и во времени величина преобразуется в дискретную, квантуется, кодируется, и цифровой код отображается на цифровом отсчетном устройстве. В результате показания цифрового прибора являются дискретными во времени и квантованными по размеру, т.е. могут принимать лишь конечное число значений.

Внешним признаком аналоговых или цифровых приборов является наличие аналогового или цифрового показывающего или регистрирующего устройства. Соответственно приборы принято также разделять на показывающие, допускающие только отсчитывание показаний, и регистрирующие, в которых предусмотрена автоматическая регистрация показаний. Среди последних, в свою очередь, различают самопишущие и печатающие. В самопишущих приборах (являющихся аналоговыми) показания измеряемых значений величины записываются в виде графика осциллограммы, показывающей изменение значения величины во времени. В печатающих приборах (являющихся цифровыми) результаты измерений печатаются в цифровой форме.

Аналоговые показывающие устройства электронных приборов обычно представляют собой электромеханический преобразователь и аналоговое отсчетное устройство. Послед нее состоит из шкалы, проградуированной с помощью мерь и играющей роль меры при измерении, и указателя, совершающего линейное или угловое перемещение. В качестве указателя используются либо стрелка, либо луч света.

Цифровое отсчетное устройство обычно состоит из цифровых знаковых индикаторов, обеспечивающих воспроизведение десятичных цифр, и алфавитных индикаторов, позволяющих указать единицу измеряемой величины. В цифровых регистрирующих приборах, как правило, осуществляется печатание показаний с помощью алфавитно-цифровых печатающих устройств со скоростью до 103 знаков в секунду. Для долговременного хранения информации используются также различные виды запоминающих устройств.

Цифровое отсчетное или регистрирующее устройство никак не ограничивает точность цифрового прибора, так как цифровой код без какой-либо погрешности может быть изображен на цифровом отсчетном устройстве. Однако не всегда цифровое отсчетное или регистрирующее устройство лучше аналогового. При большом числе одновременно измеряемых величин (контроль сложного объекта) показания аналоговых приборов воспринимаются легче, так как независимо от цифр на шкале пространственное положение указателя и характер его перемещения или осциллограмма регистрируемого процесса позволяет более оперативно проводить анализ контролируемого процесса.

Для показывающих приборов обычно не требуется высокого быстродействия в силу ограниченности возможностей оператора при приеме информации.

9.Приведите пример законов распределения и доверительной вероятности нахождения погрешности в заданном интервале.

Доверительный интервал — термин, используемый в математической статистике при интервальной оценке статистических параметров, более предпочтительной при небольшом объёме выборки, чем точечная. Доверительным называют интервал, который покрывает неизвестный параметр с заданной надёжностью.

Доверительным называется интервал, в который попадают измеренные в эксперименте значения, соответствующие доверительной вероятности.

Пример 1:

Равномерное распределение вероятностей — общее название класса распределений вероятностей, возникающего при распространении идеи «равновозможности исходов» на непрерывный случай. Подобно нормальному распределению равномерное распределение появляется в теории вероятностей как точное распределение в одних задачах и как предельное — в других.

Понятие равномерного распределения первоначально появилось для дискретного множества значений случайной величины, где это понятие интуитивно наиболее просто воспринимается и означает, что каждое из этих значений реализуется с одинаковой вероятностью. Для абсолютно непрерывной случайной величины условие равной вероятности заменяется условием постоянства функции плотности. В одномерном случае это означает, что вероятность попадания случайной величины в любой допустимый промежуток фиксированной длины одна и та же и зависит только от его длины. В результате дальнейшего обобщения понятие равномерного распределения было перенесено на многомерные распределения, а также распределения, заданные в общем виде как вероятностная мера.

Пример 2:

12 Следующая ⇒