ВЫБОРОЧНЫЙ МЕТОД

ВЫБОРОЧНЫЙ МЕТОД

Выборочное наблюдение–это наиболее распространенный и совершенный вид несплошного наблюдения.

Выборочным называют такое наблюдение, которое на основе обследования части единиц совокупности дает характеристику всей совокупности. Наблюдение организуется таким образом, что эта часть отобранных для наблюдения единиц в уменьшенном масштабе репрезентирует (представляет) всю совокупность.

Совокупность, из которой производится отбор, называется генеральной, и все ее обобщающие показатели – генеральными.

Совокупность отобранных для наблюдения единиц именуют выборочной совокупностью, и все ее обобщающие показатели - выборочными.

Соотношение объемов выборки и генеральной совокупности, выраженное в процентах, называется процентом выборки.

Имеется ряд причин, в силу которых, во многих случаях выборочному наблюдению отдается предпочтение перед сплошным. Применение выборочного наблюдения дает возможность лучше организовать наблюдение, обеспечивает быстроту проведения наблюдения, приводит к экономии средств и затрат труда на получение и обработку информации.

Различают следующие виды отбора единиц наблюдения в выборочную совокупность:

- случайный;

- механический;

- типический;

- серийный.

Случайный отбор.Под этим видом отбора понимают наиболее распространенный способ отбора в случайной выборке, так называемый метод жеребьевки, при котором каждая из единиц имеет одинаковую вероятностьпопасть в выборку.

Механический отбор.Вся совокупность разбивается на равные по объему группы по случайному признаку. Затем из каждой группы, как правило, берется одна единица. Все единицы изучаемой совокупности предварительно располагаются в определенном порядке – например, по алфавиту, местоположению и т. д., а потом, в зависимости от объема выборки, механически, через определенный интервал, отбирается необходимое количество единиц. Так, если надо провести 10%-ную механическую выборку студентов, то составляется список их фамилий по алфавиту и механически отбирается каждый десятый студент, например: 1-й,11-й,21-й и т.д.

Типический отбор. Изучаемая совокупность разбивается по существенному, типическому признаку на качественно однородные, однотипные группы. Затем из каждой группы случайным способом отбирается количество единиц, пропорциональное удельному весу группы во всей совокупности.

Серийный (гнездовой) отбор. Отбору подлежат не отдельные единицы совокупности, а целые группы (серии, гнезда), отобранные случайным или механическим способом. В каждой такой группе, серии проводится сплошное наблюдение, а результаты переносятся на всю совокупность.

Точность выборки зависит и от схемы отбора. Выборка может быть проведена по схеме повторного и бесповторного отбора.

Повторный отбор. Каждая отобранная единица или серия возвращается во всю генеральную совокупность и может вновь попасть в выборку.

Бесповторный отбор. Каждая обследованная единица изымается и не возвращается в совокупность, поэтому она не попадает в повторное обследование.

Основные характеристики параметров генеральной и выборочной совокупностей обозначаются символами:

N - объем генеральной совокупности (число входящих в нее единиц);

n - объем выборки (число обследованных единиц);

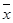- генеральная средняя (среднее значение признака в генеральной

совокупности);

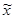- выборочная средняя;

p- генеральная доля ( доля единиц, обладающих данным значением

признака в общем числе единиц генеральной совокупности);

w - выборочная доля.

Так как при выборочном обследовании изучению подвергается не вся совокупность, а часть ее, то характеристики, получаемые при исследовании выборки, будут отличаться на определенную величину (ошибку) от аналогичной характеристики в генеральной совокупности. Ошибки выборки являются переменными величинами и могут принимать различные значения в зависимости от числа единиц совокупности, способа отбора и однородности совокупности. Среднюю в генеральной совокупности можно определить по формуле:

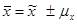где μ_x – средняя ошибка выборки.

Достоверность такого равенства равна 68,3%, т.е. в 683 случаях из 1000 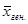(среднее значение признака в генеральной совокупности) не выйдет за пределы:

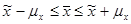Аналогичным образом может быть записан доверительный интервал генеральной доли:

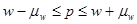
Чтобы повысить достоверность, среднюю ошибку удваивают или утраивают, т.е. раздвигают пределы возможного варьирования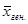

Такая ошибка называется предельной ошибкой выборки и определяется равенством:

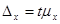где t – нормированное отклонение – «коэффициент доверия», зависящий от вероятности, с которой гарантируется ошибка выборки.

Приведем некоторые значения t, применяемые наиболее часто в выборочных наблюдениях:

Вероятность (Р)	0,6827	0,8664	0,9545	0,9973	0,9999
коэффициент доверия (t)		1,5			3,9

Когда вероятность близка к единице, выборка весьма надежна. Поэтому в практических расчетах, как правило, заданная вероятность все же должна быть не менее 0,9545.

Выборочное наблюдение проводится в целях распространения выводов, полученных по данным выборки, на генеральную совокупность. Одной из основных задач является оценка по данным выборки исследуемых характеристик (параметров) генеральной совокупности.

Предельная ошибка выборки позволяет определить предельные значения характеристик генеральной совокупности и их доверительные интервалы:

· для средней ; ;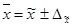

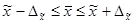· для доли ; .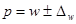

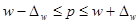Это означает, что с заданной вероятностью можно утверждать, что значение генеральной средней следует ожидать в пределах от 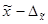до .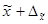

Аналогичным образом может быть записан доверительный интервал генеральной доли: ; .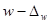

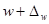Ошибки выборки различны в зависимости от способа отбора, однородности совокупности и определяются по различным формулам:

для средней:

Выборки	Собственно-случайная выборка	Типическая выборка	Серийная выборка
Повторная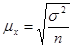
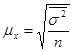
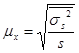
Бесповторная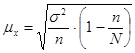

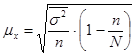
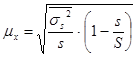
для доли:

Повторная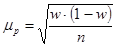
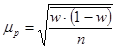
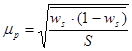
Бесповторная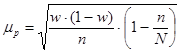

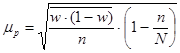
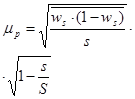
Условные обозначения:

σ² – дисперсия признака в совокупности;

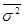- средняя из выборочных дисперсий типических групп;

σ_s² – межсерийная дисперсия;

s – число выборочных серий;

S – число равных серий в генеральной совокупности;

w – доля единиц, обладающих данным признаком;

(1-w) – доля единиц, не обладающих данным признаком;

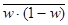- средние из частных показателей по группе;

w_s – доля данного признака в среднем по всем обследованным сериям.

При проведении выборочного наблюдения с заранее заданным значением допустимой ошибки выборки очень важно правильно определить численность (объем) выборочной совокупности, которая с определенной вероятностью обеспечит заданную точность результатов наблюдения.

Формулы для определения, необходимой численности выборки (при заданных условиях) выводятся из приведенных выше формул ошибок выборки. Так, из формул предельной ошибки выборки для повторного отбора (предварительно возведя в квадрат обе части равенства) можно выразить необходимую численность выборки:

· для средней ;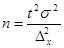

· для доли .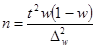

Аналогично из формул предельной ошибки выборки для бесповторного набора находим, что

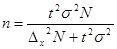(для средней);

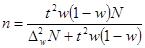(для доли).

Рассмотрим решение некоторых задач к этой теме с применением вышеуказанных формул.

Задача 1. Из партии муки поступившей на хлебозавод было взято 20 проб на влажность в порядке случайной повторной выборки. В результате проверки средняя влажность муки составила 6% при среднем квадратическом отклонении 1%.

Определить: а) среднюю ошибку выборки; б) с вероятностью, равной 0,954, предельные значения генеральной средней.

Решение:

а) формула средней ошибки выборки: .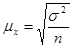

По условию n = 20, σ =1, отсюда: %.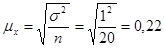

б) формула предельной ошибки выборки: 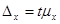. Из представленных значений ( см. с. 57 ) для вероятности Р =0,954 находим t =2, отсюда:

Δ= 2 ^.0,22 = 0,44 %, или 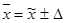= 6 % 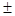0,44 %, т.е. предельные значения влажности муки определяются как 5,56 % 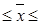6,44 %.

Задача 2. При выборочном обследовании 40 хозяйств из 800, имеющихся в регионе, установлено, что 6 хозяйств нуждаются в известковании почв.

Требуется с вероятностью 0,954 определить долю хозяйств, нуждающихся в известковании почв, во всем регионе.

Решение. Выборочная доля (доля хозяйств, нуждающихся в известковании почв, среди обследованных) равна: .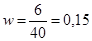

По представленным ранее данным для вероятности 0,954 находим t = 2 (см. с. 57). Предельную ошибку доли определяем по формуле бесповторного отбора:

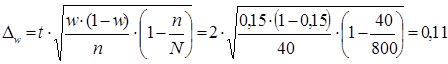Доверительные интервалы для генеральной доли:

0,15 - 0,11 ≤ p ≤ 0,15 + 0,11;

0,04 ≤ p ≤ 0,26, или 4 % ≤ p ≤ 26 %

Таким образом, с вероятностью 0,954 можно утверждать, что доля хозяйств нуждающихся в известковании почв, колеблется от 4% до 26%.

Задача 3. Сколько рабочих предприятия нужно обследовать в порядке случайной выборки для определения средней заработной платы, чтобы с вероятностью, равной 0,997, можно было гарантировать ошибку выборки не более 50 руб.? Предварительно установлено, что среднее квадратическое отклонение заработной платы равно 200 руб. Общая численность рабочих предприятия составляет 1200 человек.

Решение. Рассчитаем необходимую численность выборки, чел., по формуле бесповторного отбора 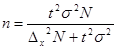, учитывая, что t =3 при Р= 0,997:

n = .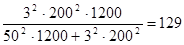

Таким образом, выборка численностью 129 чел. обеспечит заданную

точность при проведении бесповторного отбора.