
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Выполнять задания, которые выделены жирно.
Задание на 18.11 по Алгебре.
Выполнять задания, которые выделены жирно.
В задачах 41 – 50, пользуясь схемой Горнера, разделить многочлен f(x) на линейный двучлен х – с и найти значение многочлена f(x) при х = с:
41. f(x) = x4 – 2x3 + 4x2 – 6x +8, c = 1.
42. f(x) = 2x5 – 5x3 – 8x, c = -3.
43. f(x) = 3x5 + x4 – 19x2 – 13x – 10, c = 2.
44. f(x) = x4 – 3x3 – 10x2 + 2x + 5, c = -2.
45. f(x) = x5, c = 1.
46. f(x) = x4 + 2x3 – 3x2 – 4x + 1, c = -1.
47. f(x) = x4 – 8x3 + 24x2 – 50x + 90, c = 2.
48. f(x) = x4 + 2ix3 – (1 + i)x2 – 3x + 7 + i, c = -i.
49. f(x) = x4+(3–8i)x3–(21+18i)x2–(33–20i)x+7+18i, c = -1 + 2i.
50. f(x) = x5 + (1 – 2i)x4 – (3 + i)x2 + 7i, c = -1 + 2i.
В задачах 51 – 55 найти остаток от деления многочлена f(x) и φ(х), не применяя теорему о делении с остатком:
51. f(x) = x243 + x81 + x27 + x9 + x3 + x + 1, φ(x) = x2 – 1.
52. f(x) = x243 + x81 + x27 + x9 + x3 + x + 1, φ(x) = x2 + 1.
53. f(x) = x105 + x + 1, φ(x) = x2 – 1.
54. f(x) = x99 – 3x98 + x2 + 1, φ(x) = x2 – 4x + 3.
55. f(x) = x100 + 2x99 – 3x3 + 2x + 5, φ(x) = x2 + x – 2.
56. Многочлен f(x) при делении на х – 2 и х – 3 дает соответственно остатки 5 и 7. Найти остаток от деления этого многочлена на (х – 2)(х – 3).
57. При делении f(x) на х – 1, х – 2 и х + 1 остатки соответственно равны 3, 15 и 0. Найти остаток от деления f(x) на х3 – 2х2 – х + 2.
58. Многочлен f(x) при делении на х – 1, х – 2, х – 3 и на х – 4 дает соответственно остатки 1, 3, 5 и 6. Найти остаток при делении этого многочлена на произведение (х – 1)(х – 2)(х – 3)(х – 4).
59. Найти при каких значениях а многочлен f(x) = x5 –ax2 –ax +1 делится на (х + 1)2.
60. При каких значениях a и b многочлен f(x) = x3 + ax2 +bx + ab при делении на х – 2 даёт остаток 15 а при делении на х + 1 – остаток 0?
В задачах 61 – 70 найти кратность корня х0 для многочлена f(x).
61. f(x) = x5 – 8x4 + 25x3 – 38x2 + 28x – 8, x0 = 2.
62. f(x) = 2x4 + 17x3 + 45x2 + 27x – 27, x0 = -3.
63. f(x) = 4x4 – 7x2 – 5x – 1, x0 = .
64. f(x) = x5 + 7x4 + 16x3 + 8x2 – 16 – 16, x0 = -2.
65. f(x) = x6 – 9x5 + 33x4 – 65x3 + 74x2 – 46x + 12, x0 = 1.
66. f(x) = x6 + 9x5 + 30x4 + 40x3 – 48x – 32, x0 = -2.
67. f(x) = 2x5 – 13x4 + 26x3 – 24x2 + 24x – 9, x0 = 3.
68. f(x) = x6 + 7x5 + 17x4 + 13x3 – 10x2 – 20x – 8, x0 = -2.
69. f(x) = x5 – 5x4 + 4x3 +4x2 +3x + 9, x0 = 3.
70. f(x) = x5 + x4 – 6x3 – 14x2 – 11x – 3, x0 = -1.
В задачах 71 – 80, пользуясь схемой Горнера, разложить многочлен f(x) по степеням х – с. Найти значения многочлена f(x) и его производных при х = с.
71. f(x) = x4 + 3x3 – 4x2 + 6x – 5, c = -2.
72. f(x) = 3x4 + 8x3 – 2x2 + 6x – 5, c = -3.
73. f(x) = x4 – 4x3 + 6x2 + 2x +8, c = 2.
74. f(x) = x5 – 4x3 + 6x2 – 8x + 10, c = 2.
75. f(x) = x4 + 9x3 + 27x2 + 32x + 13, c = -3.
76. f(x) = 2x4 + 3x3 + 3x – 4, c = -2.
77. f(x) = x3 + 5x2 – 7x – 3, c = 4.
78. f(x) = x5 – 4x3 + 6x2 – 8x + 10, c = -1.
79. f(x) = x4 + 2x3 – 9x2 – 7, c = 3.
80. f(x) = 2x4 + 13x3 + 35x2 + 54x + 39, c = -2.
В задачах 81 – 90 разложить на простейшие дроби данные рациональные дроби
81. 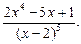
| 86. 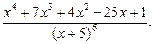
|
82. 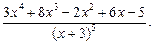
| 87. 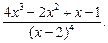
|
83. 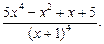
| 88. 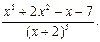
|
84. 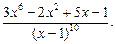
| 89. 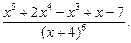
|
85. 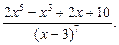
| 90. 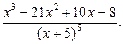
|
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|