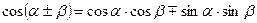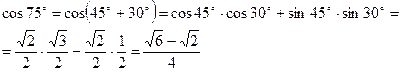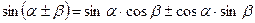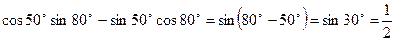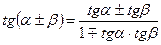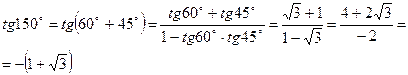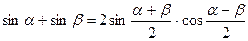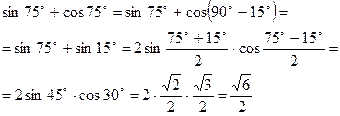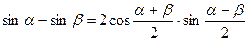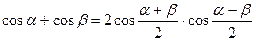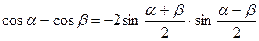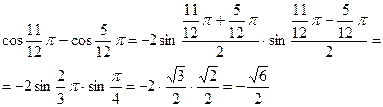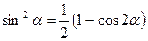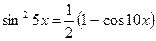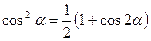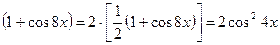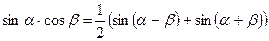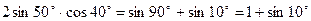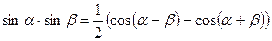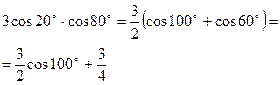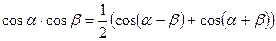- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Тригонометрические формулы. Функция. Аргумент. Примеры. Формулы суммы и разности синусов и косинусов. Формулы двойного угла. Формулы понижения степени. Произведения тригонометрических функций
Тригонометрические формулы
- Основное тригонометрическое тождество -
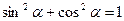
Следствия:
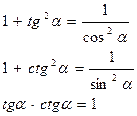
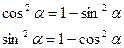
Пример 1. Найдите значения cos α, tg α, ctg α, если sin α = 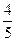 .
.
Решение: так как 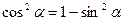 ,то
,то 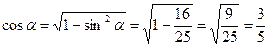 .
.
Используя соотношения 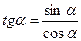 и
и 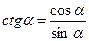 имеем:
имеем: 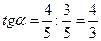 и
и 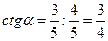 .
.
- Формулы приведения.
Значение тригонометрических функций острых углов можно вычислить по таблице. Возникает проблема для вычисления тригонометрических функций для аргумента, большего 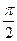 . Для этой цели существуют формулы приведения. Формулы приведения позволяют заменить тригонометрические функции больших значений аргументов тригонометрическими функциями острого угла.
. Для этой цели существуют формулы приведения. Формулы приведения позволяют заменить тригонометрические функции больших значений аргументов тригонометрическими функциями острого угла.
Функция
Аргумент
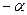
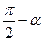

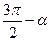
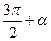
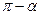
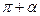
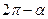
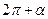
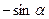
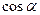
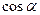
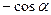
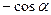
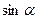
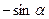
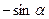
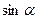
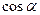
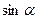
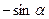
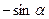
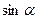
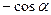
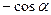
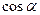
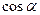

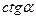
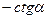
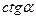
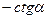

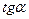

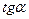
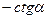
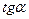

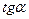

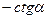
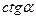
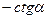
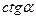
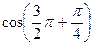 . По таблице находим, что
. По таблице находим, что 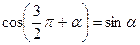 .
.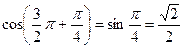 .
.