Практическая работа № 20.. Методические рекомендации.

Практическая работа № 20.

Тема: Решение тригонометрических уравнений.

Цель:Применение знаний к решению задач.

Методические рекомендации.

Опр.

Уравнение называется тригонометрическим, если неизвестная величина входит в него как аргумент тригонометрической функции.

Уравнения вида sin x = a , cos x = a , tg x = a называются простейшими. Для них выведены формулы корней:

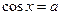
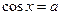
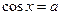sin x = a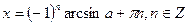

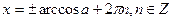
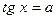
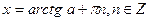
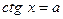
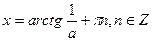
К этим уравнениям сводятся все другие. Для большинства таких уравнений требуется применение различных формул и преобразование тригонометрических выражений.

1. Уравнения, сводящиеся к квадратным 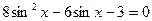. Вводят новую переменную sin x= t

2. Уравнения вида 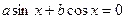а ≠ 0, b ≠ 0 называются однородными относительно sin x и cos x. Оно решается делением обеих частей на cos x ≠ 0 . В результате получается уравнение

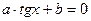. Этим же способом решается уравнение 2 sin²x – 5 sin x · cos x + 3 cos ²x = 0 . Обе части уравнения делятся на cos ²x или sin ²x .

3.Уравнения, решаемые разложением левой части на множители

Пример

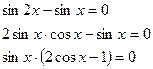Общий множитель sin x выносится за скобки.

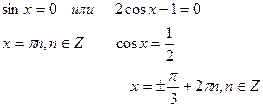
Ответ: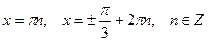

Если уравнение имеет две серии корней, полученных при решении тригонометрических уравнений, имеющую общую часть, в ответе можно оставлять обе серии. Например, х = πn ; x =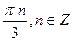

Литература:

1. Ш.А.Алимов «Алгебра и начала анализа» 10-11 кл. , стр. 165-190