
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
УРАВНЕНИЯ МАТЕМАТИЧЕСКОЙ ФИЗИКИ
УРАВНЕНИЯ МАТЕМАТИЧЕСКОЙ ФИЗИКИ
Задания для расчётно-графической работы
Задача 1. Определить тип уравнения и привести его к каноническому виду.
1.1. 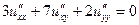 . .
| 1.2. 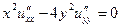 . .
|
1.3. 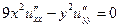 . .
| 1.4. 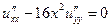 . .
|
1.5. 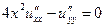 . .
| 1.6. 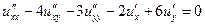 . .
|
1.7. 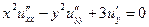 . .
| 1.8. 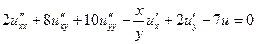 . .
|
1.9. 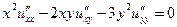 . .
| 1.10. 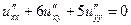 . .
|
1.11. 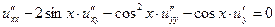 . .
| 1.12. 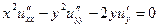 . .
|
1.13. 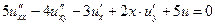 . .
| 1.14. 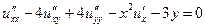 . .
|
1.15. 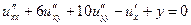 . .
| 1.16. 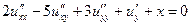 . .
|
1.17. 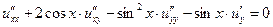 . .
| 1.18. 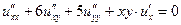 . .
|
Задача 2. Найти решение 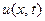 уравнения
уравнения 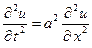 , удовлетворяющее начальным условиям
, удовлетворяющее начальным условиям
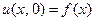 ,
, 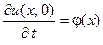 ,
, 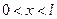
и граничным условиям
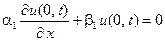 ,
, 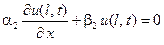 ,
, 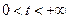 ,
,
где 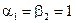 ,
, 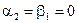 для нечётных вариантов;
для нечётных вариантов; 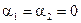 ,
, 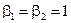 для чётных вариантов. Вид функций
для чётных вариантов. Вид функций 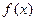 и
и 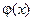 изображён на рисунках.
изображён на рисунках.
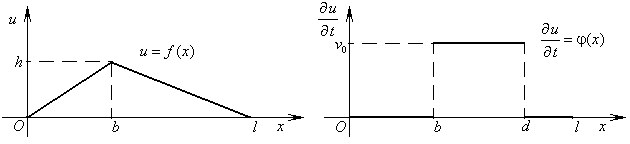
|
| № | 
| 
| 
| 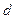
| № | 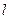
| 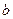
| 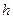
| 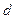
|
| 2.1. | 1,00 | 0,02 | 0,0098 | 0,42 | 2.2. | 2,00 | 0,08 | 0,0768 | 0,88 |
| 2.3. | 3,00 | 0,18 | 0,2538 | 1,38 | 2.4. | 4,00 | 0,32 | 0,5888 | 1,92 |
| 2.5. | 5,00 | 0,50 | 1,1250 | 2,50 | 2.6. | 1,00 | 0,12 | 0,0528 | 0,52 |
| 2.7. | 2,00 | 0,28 | 0,2408 | 1,08 | 2.8. | 5,00 | 2,90 | 3,0450 | 4,90 |
| 2.9. | 4,00 | 0,72 | 1,1808 | 2,32 | 2.10. | 5,00 | 0,90 | 1,8450 | 2,90 |
| 2.11. | 1,00 | 0,22 | 0,0858 | 0,62 | 2.12. | 2,00 | 0,48 | 0,3648 | 1,28 |
| 2.13. | 3,00 | 0,78 | 0,8658 | 1,98 | 2.14. | 4,00 | 1,12 | 1,6128 | 2,72 |
| 2.15. | 5,00 | 1,50 | 2,6250 | 3,50 | 2.16. | 1,00 | 0,32 | 0,1088 | 0,72 |
| 2.17. | 2,00 | 0,68 | 0,4488 | 1,48 | 2.18. | 3,00 | 1,08 | 1,0368 | 2,28 |
Задача 3. Методом Фурье найти решение 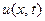 уравнения
уравнения 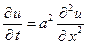 , удовлетворяющее начальному условию
, удовлетворяющее начальному условию
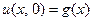 ,
, 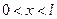
и граничным условиям
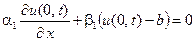 ,
, 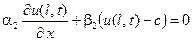 ,
, 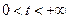 ,
,
где 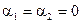 ,
, 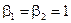 для нечётных вариантов;
для нечётных вариантов; 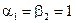 ,
, 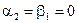 для чётных вариантов. Вид функции
для чётных вариантов. Вид функции 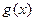 изображён на рисунке.
изображён на рисунке.
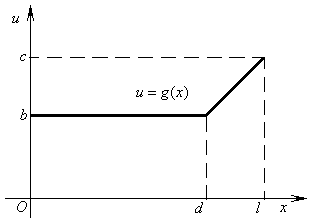
|
| № | 
| 
| 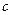
| 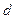
| № | 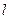
| 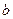
| 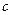
| 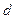
|
| 3.1. | 3,0 | 1,1 | 3,5 | 0,06 | 3.2. | 4,0 | 1,2 | 4,0 | 0,16 |
| 3.3. | 5,0 | 1,3 | 4,5 | 0,30 | 3.4. | 1,0 | 1,4 | 5,0 | 0,08 |
| 3.5. | 2,0 | 1,5 | 5,5 | 0,20 | 3.6. | 3,0 | 1,6 | 6,0 | 0,36 |
| 3.7. | 4,0 | 1,7 | 6,5 | 0,56 | 3.8. | 2,0 | 4,0 | 18,0 | 1,20 |
| 3.9. | 1,0 | 1,9 | 7,5 | 0,18 | 3.10. | 2,0 | 2,0 | 8,0 | 0,40 |
| 3.11. | 3,0 | 2,1 | 8,5 | 0,66 | 3.12. | 4,0 | 2,2 | 9,0 | 0,95 |
| 3.13. | 5,0 | 2,3 | 9,5 | 1,30 | 3.14. | 1,0 | 2,4 | 10,0 | 0,28 |
| 3.15. | 2,0 | 2,5 | 10,5 | 0,60 | 3.16. | 3,0 | 2,6 | 11,0 | 0,96 |
| 3.17. | 4,0 | 2,7 | 11,5 | 1,36 | 3.18. | 5,0 | 2,8 | 12,0 | 1,80 |
Задача 4. Найти стационарное распределение температуры в прямоугольной пластинке 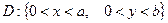 , если известны значения температуры на границе пластинки:
, если известны значения температуры на границе пластинки:
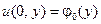 ,
, 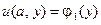
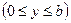 ,
,
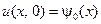 ,
, 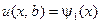
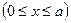 ,
,
причём 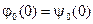 ,
,  ,
, 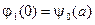 ,
, 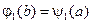 ,
, 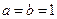 .
.
4.1. 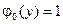 ,
, 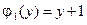 ,
, 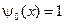 ,
, 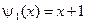 .
.
4.2. 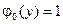 ,
, 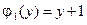 ,
, 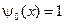 ,
, 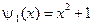 .
.
4.3. 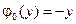 ,
, 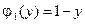 ,
, 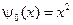 ,
, 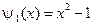 .
.
4.4. 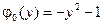 ,
, 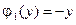 ,
, 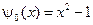 ,
, 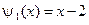 .
.
4.5. 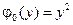 ,
, 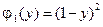 ,
, 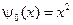 ,
, 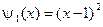 .
.
4.6. 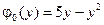 ,
, 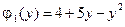 ,
, 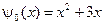 ,
, 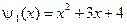 .
.
4.7. 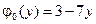 ,
, 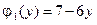 ,
, 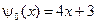 ,
, 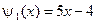 .
.
4.8. 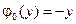 ,
, 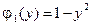 ,
, 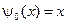 ,
, 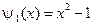 .
.
4.9. 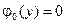 ,
, 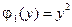 ,
, 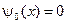 ,
, 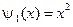 .
.
4.10. 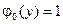 ,
, 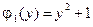 ,
, 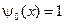 ,
, 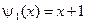 .
.
4.11. 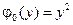 ,
, 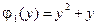 ,
, 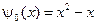 ,
, 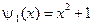 .
.
4.12. 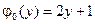 ,
, 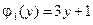 ,
, 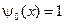 ,
, 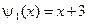 .
.
4.13. 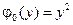 ,
, 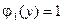 ,
, 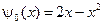 ,
, 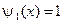 .
.
4.14. 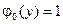 ,
, 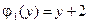 ,
, 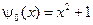 ,
, 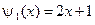 .
.
4.15. 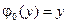 ,
, 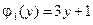 ,
, 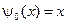 ,
, 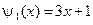 .
.
4.16. 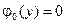 ,
, 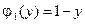 ,
, 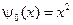 ,
, 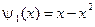 .
.
4.17. 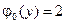 ,
, 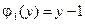 ,
, 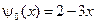 ,
, 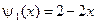 .
.
4.18. 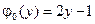 ,
, 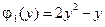 ,
, 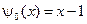 ,
, 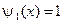 .
.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|