Преподаватель - Брыкало А.А.. Конспект урока «Математика». Группа 89 «Мастер по ремонту и обслуживанию автомобилей». Ход урока

Преподаватель - Брыкало А.А.

brukalo_aa@mail.ru

https://vk.com/id399759339

Конспект урока «Математика»

Дата 24.11.2020

Группа 89 «Мастер по ремонту и обслуживанию автомобилей»

Тема:Практическое занятие №49 «Решение задач по теме «Тела вращения»»

Форма работы:индивидуальная, электронное обучение

Тип урока:урок совершенствования знаний, умений и навыков

Продолжительность урока: 2 часа

Цель урока:

- отработать применение формул площади тел вращения при решении заданий;

- развить навыки решения задач на нахождение площади тел вращения.

Используемая литература:

Учебник: Математика. Алгебра и начала математического анализа. 10-11 классы: учебник для общеобразовательных организаций: базовый и углубленные уровни./Ш.А.Алимов, Ю.М.Колягин, М.В.Ткачева и др.- 5 изд.- М.: Просвещение, 2018г

https://uchebnikionline.ru/uchebniki/10-klass/algebra-10-11-klass-alimov-kolyagin-bazovyy-i-uglublennyy-urovni

Интернет-ресурсы:

Методика преподавания математики http://methmath.chat.ru/

Российская электронная школа https://resh.edu.ru/

Ход урока

Организационный этап:

Мотивационный модуль

Ребята, на этом уроке вы закрепите материал по теме «Тела вращения», выполнив практическую работу.

Основная часть:

Объясняющий модуль

Теоретический материал для практической работы

Соотношение между радиусом сферы, радиусом сечения и расстоянием от центра сферы до плоскости сечения:

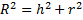
Формула для вычисления площади поверхности сферы и ее элементов:

S=4πR² – площадь сферы.

S = 2πRh – площадь поверхности сегмента сферы радиуса R с высотой h.

– площадь поверхности сектора с высотой h.

Площадь круга вычисляется по формуле: S_кр=πR².

Площадь поверхности шара вычисляется по формуле: S_сф=4πR².

Выполнение практической части работы

2.Оформление работы:

Практическое занятие № 49

Тема: «Решение задач по теме «Тела вращения»»

Цель: корректировать знания, умения и навыки по теме «Тела вращения»

Практическая часть работы:

1. Шар вписан в цилиндр. Площадь поверхности шара равна 111. Найдите площадь полной поверхности цилиндра.

2. В шар, площадь поверхности которого равна 100π, вписан цилиндр. Найти высоту цилиндра, если радиус его основания равен 4.

3. Около конуса описана сфера (сфера содержит окружность основания конуса и его вершину). Центр сферы находится в центре основания конуса. Образующая конуса равна 7√2. Найдите радиус сферы.

4. Цилиндр и конус имеют общие основание и высоту. Высота цилиндра равна радиусу основания. Площадь боковой поверхности цилиндра равна 3√2. Найдите площадь боковой поверхности конуса.

Домашнее задание:

Оформить отчет по практической работе