
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Недетерминированные конечные автоматы-распознаватели
Лекция
Недетерминированные конечные автоматы-распознаватели
1. Определение НДА
Важную роль в теории языков играют недетерминированные распознаватели, которые являются обобщением детерминированных. Недетеменированный конечный автомат-распознаватель отличается от детерменированного следующим:
1) 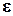 - переход, где
- переход, где 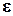 - пустой символ
- пустой символ
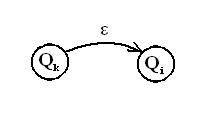
Это означает, что автомат в какой-то момент времени при условии, что он находился в состоянии 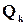 , спонтанно, без подачи на вход какого-либо символа перейти в состояние
, спонтанно, без подачи на вход какого-либо символа перейти в состояние 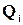 .
.
2)
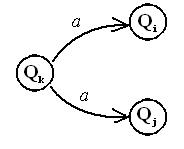
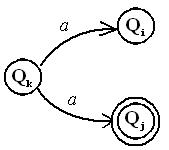
Под действием одного и того же символа автомат может перейти из состояния 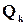 в состояние
в состояние 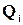 или
или 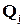 , которые не совпадают. Причем, один из этих переходов во втором примере автомата приводит в заключительное состояние, а другой - нет.
, которые не совпадают. Причем, один из этих переходов во втором примере автомата приводит в заключительное состояние, а другой - нет.
3) наличием несколько начальных состояний,
Недетерминированный автомат (НДА) - это автомат, где значение функции переходов d - не отдельное состояние, как в детерминированном автомате (ДА), а множество состояний. В общем случае у НДА может быть также не одно, а множество начальных состояний (если начальное состояние не единственно, то эти состояния при изображении таблицы переходов будут помечаться стрелкой).
Способ представления конечных распознавателей с помощью таблицы переходов легко распространяется и на представление недетерминированных конечных распознавателей.
Необходимо сделать лишь два изменения:
- во-первых, каждый элемент таблицы может не одно состояние как в детерминированном автомате, а множество состояний. Мы указываем это множество, просто перечисляя его элементы и не заключая их в скобки.
- второе изменение состоит в том, что начальные состояния указываются с помощью стрелок, расположенных перед метками соответствующих строк. Если таких стрелок нет, подразумевается, что есть только одно начальное состояние, соответствующее первой строке.
Пример. 
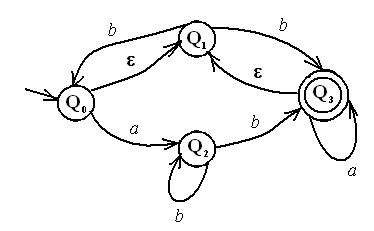
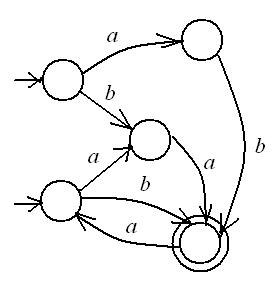
Рис. 1 Недетерминированный конечный автомат-распознаватель с ε-переходами
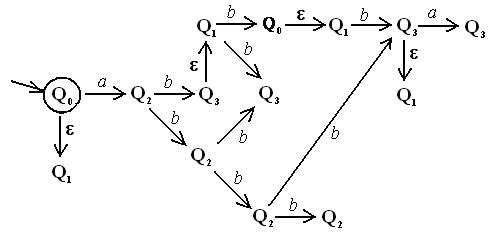
Рис. 2 Возможные поведения этого автомата при подаче входной цепочки abbba
-------------------------------------------------------
Пример.Пусть задан недетерминированный конечный автомат-распознаватель с ε-переходами:

Определить возможные поведения этого автомата при подаче входной цепочки bbab.
Автомат на рисунке а), находясь в начальном состоянии Q0, может без подачи входного сигнала перейти в состояние Q1. Если на его вход подать сигнал b, то из состояния Q0 автомат переходит в состояние Q2, а из состояния Q1 нет возможных путей. При подаче на вход следующего сигнала b, автомат из состояния Q2 может перейти в любое из двух состояний, Q2 и Q3, причем из состояния Q3 он может спонтанно перейти также в состояние Q2.
На рисунке b) показаны возможные поведения этого автомата при подаче входной цепочки bbаb. На этой диаграмме хорошо видно, что автомат спонтанно может выполнить переход, помеченный пустой цепочкой ε (такие переходы определены на диаграмме вертикальными ребрами), а каждый переход, помеченный входным символом, может быть выполнен только при подаче входного символа.
Распознавание входной цепочки недетерминированным автоматом-распознавателем опирается на следующие определение.
Определение. Недетерминированный конечный автомат распознает входную цепочку α, если существует путь, помеченный символами цепочки α, из начального в одно из заключительных состояний автомата, возможно, с учетом спонтанных переходов.
Недетерминированный конечный автомат распознает язык L, если он распознает все цепочки этого языка, и только их.
Рисунок ниже представляет детерминированный автомат, распознающий тот же самый язык, что и автомат на предыдущем рисунке. Иными словами, эти два конечных автомата эквивалентны.
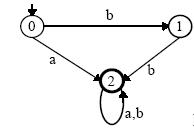
Рисунок. Детерминированный автомат, эквивалентный недетерминированному автомату рисунка 1
Таким образом, в нашем примере для недетерминированного автомата существует эквивалентный ему детерминированный конечный автомат, распознающий тот же самый язык. Оказывается, что это - общее правило:
Теорема 1. Для любого недетерминированного конечного автомата-распознавателя существует эквивалентный ему детерминированный конечный автомат-распознаватель.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|