
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Группа 1К-70/1СР-72. Тема: Преобразование суммы тригонометрических функций в произведение и произведения в сумму.. Преобразование произведения в сумму. Преобразование суммы в произведение
Группа 1К-70/1СР-72
Тема: Преобразование суммы тригонометрических функций в произведение и произведения в сумму.
Задание:
1. Изучить теоретические сведения и законспектировать их.
2. Записать примеры выполнения заданий.
3. Выполнить задания.
4. Выполненные задания сфотографировать и отправлять на электронную почту tryufelka83@mail.ru или в ЛС https://vk.com/tryufelka83 социальной сети VKontakte.
5. Выполненные задания сдать до: 01.12
Учебник: Алимов Ш.А. и др. Математика: алгебра и начала математического анализа, геометрия. Алгебра и начала математического анализа (базовый и углубленный уровни).10—11 классы. — М., 2014.
Ссылка на учебник онлайн:
https://uchebnik-skachatj-besplatno.com/Алгебра/Учебник%20Алгебра%2010-11%20класс%20Алимов%20Колягин/index.html#prettyPhoto
С. 161-163
Преобразование произведения в сумму
Запишем теперь две формулы сложения:
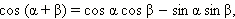
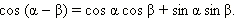
Сложим их:
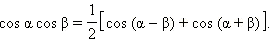
Вычтем их:
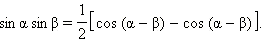
Если рассмотреть две другие формулы сложения:
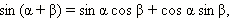
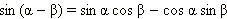 и сложить их, то получится
и сложить их, то получится
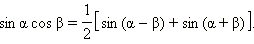
Три полученные формулы называются формулами преобразования произведения в сумму.
Преобразование суммы в произведение
Перепишем первую из полученных формул преобразования произведения в сумму в виде
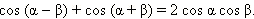
Сделаем замену переменных: x = α – β, y = α + β. Из этой замены следует, что 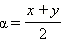 и
и 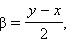 и последняя формула имеет вид
и последняя формула имеет вид
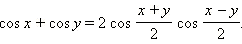
Совершенно аналогично получаются другие формулы преобразования суммы в произведение .
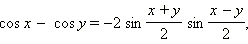
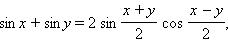
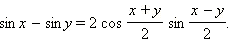
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|