ноября, классы 7 А, Б, В, Г. Геометрия. Тема «Треугольники». Рассмотрим виды треугольников.

10 ноября, классы 7 А, Б, В, Г

Геометрия

Тема «Треугольники»

Уважаемые ребята! Ознакомьтесь с темой, запишите себе в тетрадь материал, выделенный красным цветом.

Вы уже познакомились с основными геометрическими фигурами:

· прямая;

· точка;

· отрезок.

Рассмотрим геометрическую фигуру, которая также является одной из основополагающих– треугольник.

Треугольник – геометрическая фигура, образованная тремя точками, не лежащими на одной прямой, которые соединены между собой отрезками.

Точки, с которых начиналось построение, называются вершинами треугольника.

Отрезки, соединяющие вершины треугольника, называются сторонами треугольника.

А, В, С – вершины треугольника АВС.

АВ, ВС, СА – стороны треугольника АВС.

∠А,∠В,∠С – углы треугольника АВС.

Обозначение:

∆АВС

Периметр треугольника – это сумма длин всех его сторон.

Р = АВ + ВС + СА.

Рассмотрим виды треугольников.

Их можно разделить по виду и соотношению углов, а также по соотношению сторон.

По углам треугольник может быть:

– остроугольным, если все его углы являются острыми, (т.е. меньше 90°).

– тупоугольным, если один из его углов тупой(т.е. больше 90°).

– прямоугольным, если один угол 90° (т.е. прямой).

(Начертить в тетради таблицу)

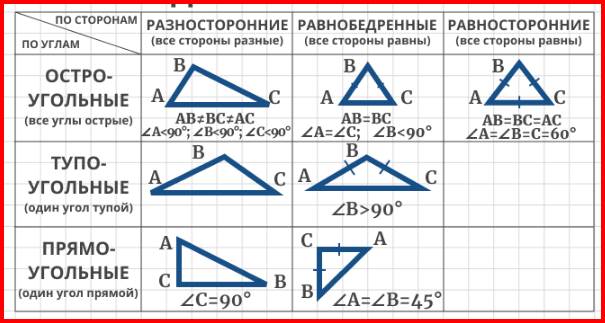
По сторонам треугольник бывает:

– разносторонний, если все его стороны имеют различную длину;

– равнобедренный, если две его стороны равны между собой;

– равносторонний, если у него все три стороны равны между собой.

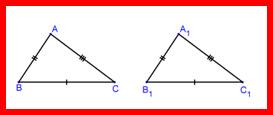
Напомним, что две фигуры, в том числе и треугольник, можно сравнить. ∆ АВС = ∆ А₁В₁С₁

∠А =∠А₁

∠В =∠В₁

∠С =∠С₁

АВ = А₁В₁

АС = А₁С₁

ВС = В₁С₁

Два треугольника называются равными, если их можно совместить наложением. При этом попарно совмещаются вершины, углы и стороны треугольников.

Следует помнить, что если два треугольника равны, то элементы (стороны и углы) одного треугольника соответственно равны элементам (сторонам и углам) другого треугольника.

Свойство равных треугольников.

В равных треугольниках против соответственно равных сторон лежат равные углы. Обратное утверждение тоже верно: против соответственно равных углов лежат равные стороны.

∆АВС=∆А₁В₁С₁

АС=А₁С₁<=>∠В =∠В₁

Равенство треугольников также можно установить, не производя наложения фигур друг на друга, а сравнивая лишь некоторые элементы этих фигур. Это станет возможным при изучении признаков равенства треугольников.

Домашнее задание П.14 №87, 88, 90

Домашнее задание высылать на адрес casanova04@yandex.ru, в графе «тема» указывать свою фамилию и класс.

Класс	Время до которого надо прислать домашние работы	Фамилии учеников, присылающих задание
7А	Вторник-среда с 9:00 до 18:00	Безрядина Яна, Куликов Станислав, Строева Татьяна, Уразова Карина, Щеглеватых Анастасия
7Б	Вторник-среда 9:00 до 18:00	Бахметьева Олеся, Калинин Дмитрий, Ренкез Кирилл, Тюрина Дарина, Урусов Виталий
7В	Вторник-среда 9:00 до 18:00	Косарева Мария, Цепляев Игорь, Чикалюк Семен,Щербатых Виктория
7Г	Вторник-среда 9:00 до 18:00	Меркулова Диана, Целихин Сергей, Беседин Илья,Насонова Ольга, Гайдаржи Кира