
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Практическая работа №25. Тема: Вычисление значений обратных тригонометрических функций. (2 часа). Краткие теоретические сведения. На чертежах красными дугами показано какие значения углов можно брать для различных тригон-х функций.
Практическая работа №25
Тема: Вычисление значений обратных тригонометрических функций. (2 часа)
Написать конспект, разобрать примеры, выполнить самостоятельную работу. Можете использовать тригонометрическую окружность. Важная тема!
Краткие теоретические сведения
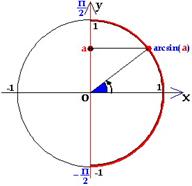
Арксинусом числа аназывается угол из отрезка 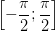 ,
синус которого равен числу а.
Свойство арксинуса от отрицательного угла: ,
синус которого равен числу а.
Свойство арксинуса от отрицательного угла:
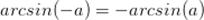
| 
|
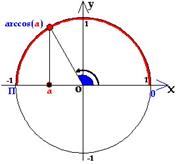
Арккосинусом числа аназывается угол из отрезка 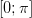 ,
косинус которого равен числу а.
Свойство арккосинуса от отрицательного угла: ,
косинус которого равен числу а.
Свойство арккосинуса от отрицательного угла:
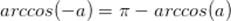
| 
|
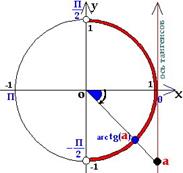
Арктангенсом числа аназывается угол из интервала 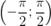 ,тангенс которого равен числу а.
Свойство арктангенса
отрицательного угла: ,тангенс которого равен числу а.
Свойство арктангенса
отрицательного угла:
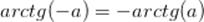
| 
|
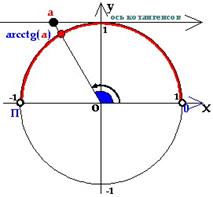
Арккотангенсом числа аназывается угол
из интервала 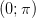 , котангенс которого равен числу а.
Свойство арккотангенса от отрицательного угла , котангенс которого равен числу а.
Свойство арккотангенса от отрицательного угла
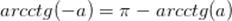
| 
|
На чертежах красными дугами показано какие значения углов можно брать для различных тригон-х функций.
| Значения функции: | Значения аргумента: |
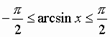
| 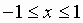
|
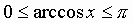
| 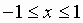
|
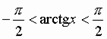
| 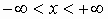
|
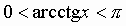
| 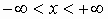
|
|
Ф-ция | Значения | ||||||||
| t =0 | t = 
| t = 
| t = 
| t = 
| t = 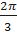
| t = 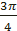
| t = 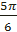
| t = 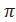
| |
| sin t | 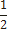
| 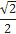
| 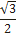
| ||||||
| cos t | 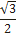
| 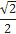
| 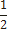
| 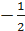
| 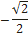
| 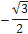
| - 1 | ||
| tg t | 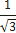
| 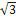
| __ | ||||||
| ctg t | Не сущ | 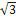
| 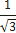
| - 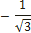
| - 1 | - 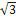
| Не сущ | ||
Рассмотрим решение нескольких примеров:
Пример 1. Найти 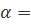 arcsin
arcsin  .
.
Решение. Существует бесчисленное множество аргументов, синус которых равен  . ,
. ,
например: 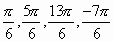 и т.д. Но нас интересует только тот аргумент, который находится на отрезке
и т.д. Но нас интересует только тот аргумент, который находится на отрезке 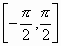 . Таким аргументом будет
. Таким аргументом будет 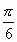 . Итак, arcsin
. Итак, arcsin 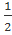 =
=  .
.
Пример 2. Найти arcsin 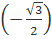 .
.
Решение. Рассуждая так же, как и в примере 1, получим .
Пример 3.Найти arctg 1 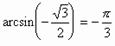
Решение: arctg 1= 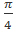 , так как tg
, так как tg 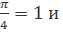
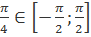
Пример 4. Найти аrcctg 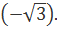
Решение. аrcctg 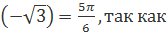 ctg
ctg 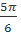 =
= 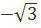 и
и 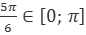 .
.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|