Раздел 3. Прямые и плоскости в пространстве

26.11.20 г.

Раздел 3. Прямые и плоскости в пространстве

Тема 3.3. Геометрические преобразования

Параллельное проектирование. Площадь ортогональной проекции.

Изображение пространственных фигур

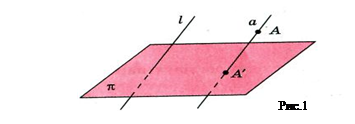
Точка А` является параллельной проекцией точки А на плоскость π в направлении прямой ℓ. Если точка А принадлежит прямой ℓ, то параллельной проекцией А на плоскость π считается точка пересечения прямой ℓ с плоскостью π. Такое соответствие называется параллельным проектированием (рис. 1).

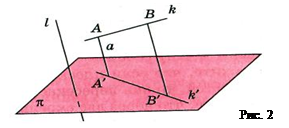
Свойство №1. Если прямая параллельна или совпадает с прямой ℓ, то её проекцией в направлении этой прямой является точка. Если прямая не параллельна и не совпадает с прямой ℓ, то её проекцией является прямая (рис. 2).

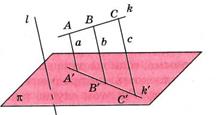
Свойство №2. Проекция отрезка при параллельном проектировании есть точка или отрезок в зависимости от того, лежит он на прямой, параллельной или совпадающей с прямой ℓ, или нет. Отношение длин отрезков, лежащих на одной прямой, сохраняется. В частности, середина отрезка при параллельном проектировании переходит в середину соответствующего отрезка (рис. 3).

Рис. 3

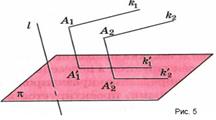
Свойство №3. Если две параллельные прямые не параллельны прямой ℓ, то их проекции в направлении ℓ могут быть или параллельными прямыми, или одной прямой (рис. 4).

Рис. 4

Ортогональное проецирование является частным случаем параллельного проецирования, когда направление проецирования S перпендикулярно плоскости проекции П.

Теорема: Площадь ортогональной проекции многоугольника на плоскость равна произведению его площади на косинус угла между плоскостью многоугольника и плоскостью проекции.

Задача 1. Даны точки (1; 2; 3), (0; -1; 2), (1; 0; -3). Постройте данные точки в пространственной системе координат.

Задача 2. Найдите значения а, b, с в формулах параллельного переноса: х' = х + а, у' = у + b, z' = z + c, если при этом параллельном переносе точка A (1; 0; 2) переходит в точку А' (2; 1; 0).