Практическая работа № 6. Задание 1.

Практическая работа № 6

ТЕМА: Структурные характеристики вариационного ряда распределения

Цель работы – закрепить теоретические знания и приобрести практические навыки в определении структурных характеристик вариационного ряда аналитическим и графическим способами, в анализе полученных результатов.

Литература: В. С. Мхитарян. Статистика, стр. 116-119

Ход работы

Задание 1.

Имеются следующие данные о возрастном составе рабочих цеха (лет):

Группы рабочих по возрасту, лет	18-21	21-24	24-27	27-30	30-33	33-36	36-39
Число рабочих

Определите моду и медиану. Представьте интервальный вариационный ряд графически в виде гистограммы, полигона и кумуляты.

Решение:

1.Определим по наибольшей частоте модальный интервал: 27-30

Рассчитаем моду по формуле: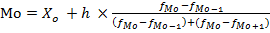

гдех_о – начальная (нижняя) граница модального интервала;

h – величина интервала;

f_Мо – частота модального интервала;

f_Мо-1 – частота интервала, предшествующая модальному;

f_Мо+1– частота интервала следующая за модальным.

Xо = 27 h = 30 - 27 = 3 f_Мо= 10

Мо =27 + 3 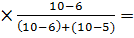28,3 лет

2.В случае интервального вариационного ряда медиану определяют по формуле:

Ме =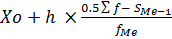

Найдем 0,5∑ƒ= (1+3+6+10+5+3+2) : 2 = 15 – это порядковый номер медианы

По накопленным суммам частот определяем, что медиана находится в интервале: 27-3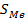0 ( = 20)

Ме = 27 + 3 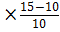= 28,5 лет

Ответ: по моде наибольшее число рабочих имеют возраст 28,3 лет; по медиане – половина рабочих моложе 28,5 лет, другая половина старше.

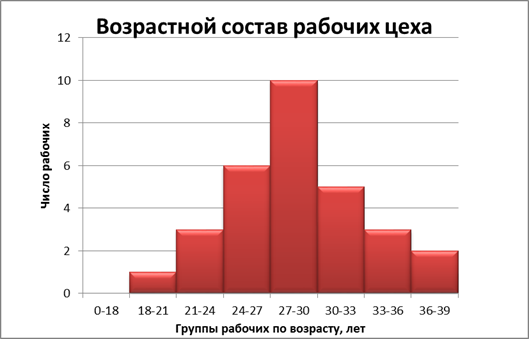
Рисунок 1. Гистограмма вариационного ряда распределения рабочих по возрасту.

Рисунок 2. Гистограмма и полигон вариационного ряда.

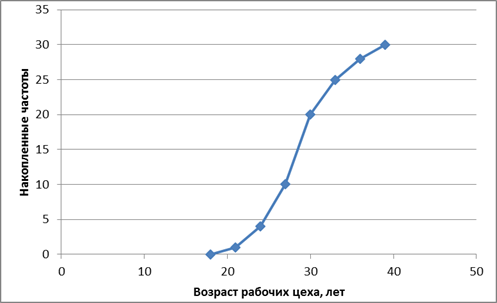
Рисунок 3. Кумулята распределения числа рабочих в зависимости от возраста.

Задание 2.

Распределение семей города по размеру среднедушевого дохода

Группы семей по размеру дохода, руб.	Число семей	Накопленные частоты	Накопленные частоты, % к итогу
До 5000
5000-6000
6000-7000
7000-8000
8000-9000
900-10000
Свыше 10000
Итого:

Рассчитать моду и медиану по данным таблицы.

Решение:

1.Модальный интервал: 7000-8000

h = 8000 – 7000 = 1000

Мо = 7000 + 1000 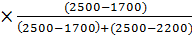= 7727,3 руб.

2. 0,5∑ƒ= 10000 : 2 = 5000

Ме = 7000 + 1000 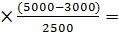7800 руб.

Ответ: по моде наибольшее число семей имеют доход 7727,3 рублей. По медиане половина семей имеют доход менее 7800 рублей, половина более этой суммы.

Задание 3. Ответить на контрольные вопросы:

1. Что такое мода в статистике и зачем она нужна?

2. Могут ли мода, медиана и средняя арифметическая совпадать?

3. Может ли ряд распределения характеризоваться двумя и более модами?

1)Мода – значение признака, наиболее часто встречающееся в исследуемой совокупности.

Используется в статистической практике при анализе покупательского спроса, регистрации цен.

2) Для одномодального симметричного ряда распределения средняя арифметическая, медиана и мода совпадают. Для асимметричных распределений они не совпадают.

3) Может двумя и более.

Вывод: Я приобрела практические навыки в определении структурных характеристик вариационного ряда.