
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Решение.. Решение.. Решение.. Решение.. Решение.. Решение.. Приведём другое решение.. Решение.
1.Найдите значение выражения 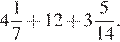
Решение.
Найдем значение выражения:
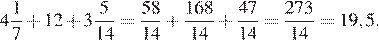
Ответ: 19,5.
2.Найдите значение выражения 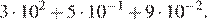
Решение.
Используем свойство степеней:
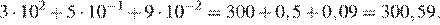
Ответ: 300,59.
3.Товар на распродаже уценили на 50%, при этом он стал стоить 820 рублей. Сколько рублей стоил товар до распродажи?
Решение.
После уценки товар стал стоить 50% или половину начальной стоимости. Следовательно, до уценки стоимость была вдвое больше и составляла 840 · 2 = 1640 руб.
Ответ: 1640.
4.Мощность постоянного тока (в ваттах) вычисляется по формуле 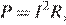 где
где 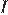 — сила тока (в амперах),
— сила тока (в амперах), 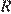 — сопротивление (в омах). Пользуясь этой формулой, найдите сопротивление
— сопротивление (в омах). Пользуясь этой формулой, найдите сопротивление 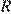 (в омах), если мощность составляет 224 Вт, а сила тока равна 4 А.
(в омах), если мощность составляет 224 Вт, а сила тока равна 4 А.
Решение.
Выразим из исходной формулы сопротивление и найдем его:
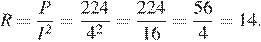
Ответ: 14.
5.Найдите значение выражения 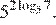
Решение.
Выполним преобразования:
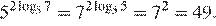
Ответ: 49.
6.В доме, в котором живёт Женя, один подъезд. На каждом этаже по восемь квартир. Женя живёт в квартире 87. На каком этаже живёт Женя?
Решение.
Разделим 87 на 8:
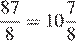 .
.
Значит, Женя живет на 11 этаже.
Ответ: 11.
Приведём другое решение.
Составим таблицу этажей.
| Этаж | Квартиры |
| 1—8 | |
| 9—16 | |
| 17—24 | |
| 25—32 | |
| 33—40 | |
| 41—48 | |
| 49—56 | |
| 57—64 | |
| 65—72 | |
| 73—80 | |
| 81—88 | |
| 89—96 |
Таким образом, Женя живёт на одиннадцатом этаже.
7.Решите уравнение 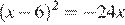 .
.
Решение.
Используем формулы квадрата разности и квадрата суммы:
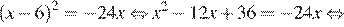
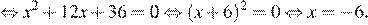
Ответ: −6.
8.  Какой наименьший угол (в градусах) образуют минутная и часовая стрелки часов в 11:00?
Какой наименьший угол (в градусах) образуют минутная и часовая стрелки часов в 11:00?
Решение.
Между 11 и 12 — 5 делений, 1 деление — 6°, поэтому 
Ответ: 30.
9.Установите соответствие между величинами и их возможными значениями: к каждому элементу первого столбца подберите соответствующий элемент из второго столбца.
| ВЕЛИЧИНЫ | ВОЗМОЖНЫЕ ЗНАЧЕНИЯ | |
| А) объём бытового холодильника Б) объём железнодорожного вагона В) объём пакета сока Г) объём воды в Ладожском озере | 1) 120 м3 2) 1,5 л 3) 908 км3 4) 300 л |
Запишите в ответ цифры, расположив их в порядке, соответствующем буквам:
| A | Б | В | Г |
Решение.
А) объём бытового холодильника — соответствует 4.
Б) объём железнодорожного вагона — соответствует 1.
В) объём пакета сока — соответствует 2.
Г) объём воды в Ладожском озере — соответствует 3.
Ответ: 4123.
10.Перед началом футбольного матча судья бросает монетку, чтобы определить, какая из команд начнёт игру с мячом. Команда «Физик» играет три матча с разными командами. Найдите вероятность того, что в этих играх «Физик» выиграет жребий ровно два раза.
Решение.
Обозначим «1» ту сторону монеты, которая отвечает за выигрыш жребия «Физиком», другую сторону монеты обозначим «0». Тогда благоприятных комбинаций три: 110, 101, 011, а всего комбинаций 23 = 8: 000, 001, 010, 011, 100, 101, 110, 111. Тем самым, искомая вероятность равна:
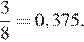
Ответ: 0,375.
11.На рисунке жирными точками показана цена платины, установленная Центробанком РФ во все рабочие дни в октябре 2010 года. По горизонтали указываются числа месяца, по вертикали — цена платины в рублях за грамм. Для наглядности жирные точки на рисунке соединены линией.
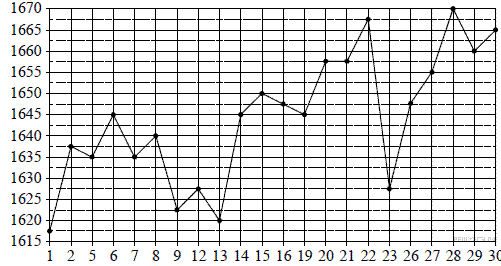
Определите по рисунку наибольшую цену платины в период с 7 по 19 октября. Ответ дайте в рублях за грамм.
Решение.
Из графика видно, что наибольшая цена платины в период с 7 по 19 октября составила 1650 рублей (см. рисунок).
Ответ: 1650.
12.Мебельный салон заключает договоры с производителями мебели. В договорах указывается, какой процент от суммы, вырученной за продажу мебели, поступает в доход мебельного салона.

В прейскуранте приведены цены на четыре софы. Определите, продажа какой софы наиболее выгодна для салона. В ответе запишите, сколько рублей поступит в доход салона от продажи этой софы.

Решение.
Рассмотрим все варианты.
При продаже софы «Анна» по цене 15 000 руб. доход салона составит 15 000  0,07 = 1050 руб.
0,07 = 1050 руб.
При продаже софы «Алевтина» по цене 22 000 руб. доход салона составит 22 000  0,035 = 770 руб.
0,035 = 770 руб.
При продаже софы «Аркадия» по цене 19 000 руб. доход салона составит 19 000  0,04 = 760 руб.
0,04 = 760 руб.
При продаже софы «Анастасия» по цене 16 500 руб. доход салона составит 16 500  0,06 = 990 руб.
0,06 = 990 руб.
Поэтому для салона наиболее выгодна продажа софы «Анна» фирмы «Альфа», доход от которой составит 1050 рублей.
Ответ: 1050.
13. 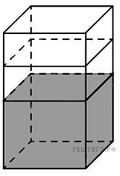 В бак, имеющий форму правильной четырёхугольной призмы со стороной основания, равной 40 см, налита жидкость. Чтобы измерить объём детали сложной формы, её полностью погружают в эту жидкость. Найдите объём детали, если уровень жидкости в баке поднялся на 5 см. Ответ дайте в кубических сантиметрах.
В бак, имеющий форму правильной четырёхугольной призмы со стороной основания, равной 40 см, налита жидкость. Чтобы измерить объём детали сложной формы, её полностью погружают в эту жидкость. Найдите объём детали, если уровень жидкости в баке поднялся на 5 см. Ответ дайте в кубических сантиметрах.
Решение.
Объем вытесненной жидкости равен объему детали (закон Архимеда). Уровень жидкости поднялся на h = 5 см, сторона основания a = 40 см, значит, вытесненный объем будет равен 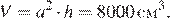 Найденный объём является объёмом детали.
Найденный объём является объёмом детали.
Ответ: 8000.
14.Установите соответствие между графиками линейных функций и графиками их производных.
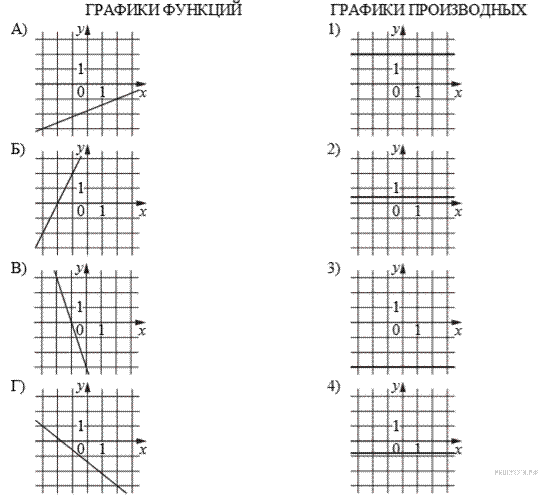
Решение.
Пусть угол, который составляет касательная с положительным направлением оси абсцисс, равен α, а угловой коэффициент касательной равен k. Тогда:
| α | k |

| 
|
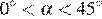
| 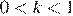
|
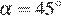
| 
|
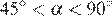
| 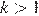
|
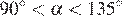
| 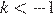
|
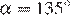
| 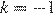
|
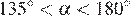
| 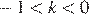
|
Значение производной в точке равно угловому коэффициенту касательной, проведённой в этой точке. Таким образом, получаем соответствие: А — 2, Б — 1, В — 3 и Г — 4.
Ответ: 2134.
15.В треугольнике 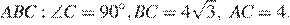 Найдите
Найдите 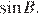
Решение.
Найдем гипотенузу треугольника: 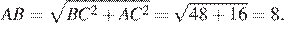 Тогда
Тогда 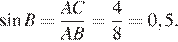
Ответ: 0,5.
16.  Объём конуса равен
Объём конуса равен 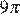 , а его высота равна
, а его высота равна  . Найдите радиус основания конуса.
. Найдите радиус основания конуса.
Решение.
Найдём радиус основания конуса по формуле:
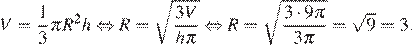
Ответ: 3.
17.На координатной прямой отмечены точки A, B, C, и D.
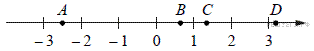
Число 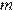 равно
равно 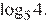
Каждой точке соответствует одно из чисел в правом столбце. Установите соответствие между указанными точками и числами.
| ТОЧКИ | ЧИСЛА | |
| А) A Б) B В) C Г) D | 1) 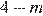 2)
2) 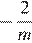 3)
3) 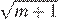 4)
4) 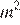
|
В таблице под каждой буквой укажите соответствующий номер.
| А | Б | В | Г |
Решение.
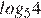 - это число меньше 1 приблизительно. Оценим остальные числа:
- это число меньше 1 приблизительно. Оценим остальные числа:
1) 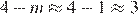 , следовательно, это точка D
, следовательно, это точка D
2) 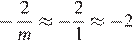 , следовательно, это точка А
, следовательно, это точка А
3) 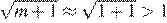 , следовательно, это точка С
, следовательно, это точка С
4) 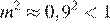 , следовательно, это точка В
, следовательно, это точка В
Ответ: 2431
18.В фирме N работает 60 сотрудников, из них 50 человек знают английский язык, а 15 — французский. Выберите утверждения, которые верны при указанных условиях.
1) Не более 15 сотрудников этой фирмы знают и английский, и французский языки.
2) Если сотрудник этой фирмы знает английский язык, то он знает и французский.
3) Хотя бы три сотрудника этой фирмы знают и английский, и французский языки.
4) В этой фирме нет ни одного человека, знающего и английский, и французский языки.
Решение.
1) Утверждение следует из данного условия, так как в сумме 65 человек, которые знают либо английский, либо французский, следовательно, 5 человек точно знают оба языка, что не противоречит утверждению.
2) Утверждение не следует из данного условия.
3) Утверждение следует из данного условия, так как 5 человек, точно, знают и английский, и французский язык.
4) Утверждение не следует из данного условия.
Ответ: 13 или 31.
19.Найдите трёхзначное число, сумма цифр которого равна 20, а сумма квадратов цифр делится на 3, но не делится на 9. В ответе укажите какое-нибудь одно такое число.
Решение.
Разложим число 20 на слагаемые различными способами:
20 = 9 + 9 + 2 = 9 + 8 + 3 = 9 + 7 + 4 = 9 + 6 + 5 = 8 + 8 + 4 = 8 + 7 + 5 = 8 + 6 + 6 = 7 + 7 + 6.
При разложении способами 1—4, 7 и 8 суммы квадратов чисел не кратны трём. При разложении пятым способом сумма квадратов кратна девяти. Разложение шестым способом удовлетворяет условиям задачи. Таким образом, условию задачи удовлетворяет любое число, записанное цифрами 5, 7 и 8, например, число 578.
20.Про натуральные числа A, B и С известно, что каждое из них больше 4, но меньше 8. Загадали натуральное число, затем его умножили на A, потом прибавили к полученному произведению B и вычли С. Получилось 417. Какое число было загадано?
Решение.
Числа А, В и С могут быть равны 5, 6 или 7.
Пусть загадали натуральное число Х, тогда Х · А + В – С = 417 или Х · А = 417 + (C – B). Рассмотрим различные случаи.
1) С – В = 0 (7 – 7 = 0, 6 – 6 = 0 или 5 – 5 = 0), тогда Х · А = 417. Число 417 не делится нацело на 5, на 6 и на 7, значит, этот случай не подходит.
2) С – В = 1 (7 – 6 = 1 или 6 – 5 = 1), тогда Х · А = 418. Число 418 не делится нацело на 5, на 6 и на 7, значит, этот случай не подходит.
3) С – В = –1 (6 – 7 = –1 или 5 – 6 = –1), тогда Х · А = 416. Число 416 не делится нацело на 5, на 6 и на 7, значит, этот случай не подходит.
4) С – В = 2 (7 – 5 = 2), тогда Х · А = 419. Число 419 не делится нацело на 5, на 6 и на 7, значит, этот случай не подходит.
5) С – В = –2 (5 – 7 = –2), тогда Х·А = 415. Число 415 делится нацело на A = 5, значит, Х = 83.
Ответ: 83.
Ключ
№ п/п
№ задания
Ответ
19,5
300,59
-6
0,375
0,5
13|31
578|587|758|785|857|875
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|