Задание:. Ряды динамики

Задание:

1. Прочитайте лекцию.

2. Выпишите в тетрадь основные понятия и формулы, к формулам запишите пояснения к условным обозначениям.

3. Устно ответьте на контрольные вопросы.

Ряды динамики

Динамические ряды и их виды

Процессы и явления общественной жизни, являющиеся предметом изучения статистики, находятся в постоянном движении и изменении.

Статистические данные, характеризующие изменения явлений во времени, называются динамическими (хронологическими или временными) рядами.Такие ряды строят для выявления и изучения складывающихся закономерностей в развитии явлений экономической, политической и культурной жизни общества.

Правильно построенный динамический ряд состоит из сопоставимых статистических показателей. Для этого необходимо, чтобы состав изучаемой совокупности был один и тот же на всем протяжении ряда, т.е. относился к одной и той же территории, к одному и тому же кругу объектов и был рассчитан по одной и той же методологии. Кроме того, данные динамического ряда должны быть по возможности одинаковыми.

Для преобразования несопоставимых рядов в сопоставимые производят пересчет данных с помощью различных приемов. Рассмотрим некоторые из них.

Прямой пересчет данных производится, например, при изучении движения населения, которые нельзя механически сравнивать без учета изменившихся

Прямой пересчет данных производится, например, при изучении движения населения, которые нельзя механически сравнивать без учета изменившихся территорий проживания. Динамика численности населения СССР в 1980 и 1999 гг. несопоставима, потому что в конце 90-х гг. территория страны изменилась. Чтобы данные стали сравнимы, необходимо численность населения СССР в 1980 г. Уменьшить на число проживающих в этот же период в отделившихся территориях, т. е. провести прямой пересчет данных, лишь тогда они будут сопоставимы и их можно будет сравнивать. Такой же пересчет требуется по другим регионам, у которых в 90-е гг. менялись территориальные границы.

Смыкание рядов используют для сопоставления двух рядов показателей, характеризующих динамику одного и того же явления в новых и старых административных границах. Если имеются данные в новых и старых границах по одному и тому же кругу объектов, то такие динамические ряды можно сомкнуть.

Виды динамических рядов.В зависимости от характера изучаемых величин различают три вида динамических рядов: моментные, интервальные и ряды средних.

Моментными рядами называются статистические ряды, характеризующие размеры изучаемого явления на определенную дату, момент времени. Примером могут служить данные о численности персонала фирмы по состоянию на первое число каждого месяца.

Следует помнить, что моментные ряды нельзя суммировать. Бессмысленно, например, складывать численность работающих по состоянию на 1 января, 1 февраля, 1 марта и т. д. Полученная сумма ничего не выражает, так как в ней многократно повторяются одни и те же показатели.

Интервальными рядами называются статистические ряды, характеризующие размеры изучаемого явления за определенные промежутки (периоды, интервалы) времени.

Вычисление средней динамической ряда.Для общей характеристики какого-либо явления за определенный период рассчитывают средний уровень из всех членов динамического ряда.

Способы его расчета зависят от вида динамического ряда. Для интервальных рядов средняя рассчитывается по формуле средней арифметической, причем при равных интервалах применяется средняя арифметическая простая, а при неравных – средняя арифметическая взвешенная.

Для нахождения средних значений моментного ряда применяют среднюю хронологическую

Средняя хронологическая моментного ряда равна сумме всех уровней ряда, поделенной на число членов ряда без одного, причем первый и последний члены ряда берутся в половинном размере.

Если интервалы между периодами не раны, то применяется средняя арифметическая взвешенная, а в качестве весов берутся отрезки времени между датами, к которым относятся парные средние смежных значений уровня.

9.2. Основные показатели анализа динамических рядов

Динамические ряды анализируются при помощи таких показателей, как уровень ряда, средний уровень, абсолютный прирост, темп роста, коэффициент роста, темп прироста, коэффициент опережения, абсолютное значение одного процента прироста.

Уровнем ряда называется абсолютная величина каждого члена динамического ряда. Понятно, что все уровни ряда характеризуют его динамику. Различают начальный, конечный и средний уровни ряда. Начальный уровень – величина первого члена ряда, конечный – последнего, средний – средняя из всех значений динамического ряда.

Абсолютный прирост характеризует размер увеличения или уменьшения изучаемого явления за определенный период времени. Он определяется как разность между данным уровнем и предыдущим или первоначальным. Уровень, который сравнивается, называется текущим , а уровень, с которым производится сравнение – базисным, так как он является базой для сравнения. Если каждый уровень ряда сравнивается с предыдущим, то получают цепные показатели. Если же все уровни ряда сравниваются с одним и тем же первоначальным уровнем, то полученные показатели называются базисными.

Для динамического ряда у₀^, у₁– у₂ … у_n-1^,у_n^, состоящего из n+1 уровней, абсолютный прирост определяется по формулам:

- цепной ∆¡ = у¡ -у¡_-1;

- базисный ∆ + у¡ - у₀^,

где у¡ - текущий уровень ряда; у¡_-1– уровень, предшествующий у¡ и у₀– начальные уровни ряда.

Средний абсолютный прирост можно рассчитать по формуле

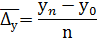
Где _у- средний абсолютный прирост; у_n– конечный уровень ряда; у₀– начальный уровень ряда.

В ряде случаев изучаемое явление растет неравномерно, под воздействием многих факторов, силы и направление влияния которых из года в год меняются. Так, размеры продукции растениеводства зависят от многих факторов, в том числе и от метеорологических условий. Поэтому для определения роста производства зерна или другой продукции растениеводства правильнее сравнивать не ежегодные уровни валового сбора урожая, а средние – за определенные периоды времени.

Для характеристики относительной скорости изменения уровня динамического ряда в единицу времени вычисляют показатели темпов роста и прироста.

Темпом роста называ6ется отношение данного уровня явления к предыдущему или начальному, выраженное в процентах. Темпы роста, вычисленные как отношение данного уровня к предыдущему, называются цепными, а к начальному – базисными.

Темпы роста вычисляются по формулам:

- цепной Т _р= 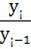* 100;

- базисный Т _р= 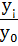* 100,

Где у_¡ - текущий уровень ряда; у_¡-1 - уровень, предшествующий у_¡и у₀– начальные уровни ряда.

Если темпы выражены в виде простых отношений, т. е. база сравнения принимается за 1, а не за 100%, то полученные показатели называются коэффициентами роста.

Темпом прироста называется отношение абсолютного прироста к предыдущему или начальному уровню, выраженное в процентах. Темп прироста можно рассчитать по данным о темпе роста. Для этого нужно от темпа роста отнять 100 или от коэффициента роста – 1, в последнем случае получим коэффициент прироста К _{пр :}

Темпы прироста рассчитываются по формулам:

- цепной Т _пр = Т _{р. ц.}-100 или (К _{р. ц.}-1) *100;

- базисный Т _пр = Т _{р. б.}-100 или (К _{р. б.}-1) * 100.

Для характеристики темпов роста и прироста в среднем за весь период, охватываемый рядом динамики, исчисляют средний темп роста и прироста. Средний темп (коэффициент) роста определяется по формуле средней геометрической. Когда средний темп роста вычисляется по абсолютным данным первого и последнего членов динамического ряда, применяется следующая формула средней геометрической

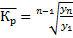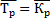*100,

где у₁– начальный уровень; у_n – конечный уровень; n – число членов ряда.

Если абсолютные данные динамического ряда отсутствуют, а имеются цепные коэффициенты роста (по сравнению с предыдущим периодом), средний коэффициент роста определяется по формуле

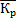
где К₁, К₂, К_{3, …}К_n - коэффициенты роста за каждый период.

При сравнении интенсивности развития явлений по данным двух динамических рядов представляет интерес определение интенсивности изменения во времени одного явления по сравнению с другим. Такое сопоставление проводится как при сравнении двух взаимосвязанных динамических рядов, характеризующих развитие изучаемых явлений, так и при сравнении рядов одних и тех же явлений, но относящихся к разным объектам и странам. Например, сравнение динамики роста производительности труда и заработной платы, сопоставление динамики роста производительности труда и заработной платы, сопоставление рядов динамики, характеризующих производство важнейших видов продукции в России и других странах, и т.д. Для этого сравнивают базисные темпы роста за одинаковые периоды времени.

Отношение базисных темпов роста двух динамических рядов за одинаковые отрезки времени называются коэффициентом опережения.Обозначим коэффициент опережения К_оп, базисные коэффициенты роста первого ряда динамики – К ^ɪ, второго – К ^ɪɪ.

Тогда

Коэффициент опережения показывает, во сколько раз быстрее растет уровень одного ряда динамики по сравнению с другим.

Отношение абсолютного прироста к темпу прироста представляет собой абсолютное значение одного процента по формуле

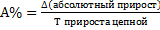Интерполяция и экстраполяция.При решении некоторых вопросов приходится определять неизвестные промежуточные значения динамического ряда. Эта задача решается способом интерполяции. Интерполяция – способ определения неизвестных промежуточных значений динамического ряда.

Интерполяция заключается по существу в приближенном отражении сложившейся закономерности внутри определенного отрезка времени – в отличие от экстраполяции, которая требует выходы за пределы этого времени.

Экстраполяция – метод определения количественных характеристик для совокупностей и явлений, не подвергшихся наблюдению, путем распространения на них результатов, полученных из наблюдения за аналогичными совокупностями за прошедшее время, на будущее т. д.

Контрольные вопросы

1. Какие задачи решаются с помощью анализа рядов динамики?

2. Назовите виды рядов динамики.

3. В каких случаях используются аналитические показатели динамического ряда? Перечислите данные показатели.

4. Дайте общую характеристику средних показателей динамического ряда.

5. Какой метод расчета среднего темпа роста уровней ряда динамики вы знаете?

6. С какой целью рассчитывается средний темп прироста?

7. В чем суть метода скользящей средней?

8. Назовите способы измерения сезонных колебаний. Как рассчитываются индексы сезонности?