
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Вывод: График функции при симметричен графику функции при относительно прямой .
| Класс | |||||||||||
| Предмет | Алгебра | ||||||||||
| Дата | 18.11.20 г. | ||||||||||
| Тема | Функция 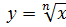 , х≥0 , х≥0
| ||||||||||
| Цель | рассмотреть свойства и графики функции 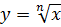 . .
| ||||||||||
| Выполните устно | Напомним основное определение.
Определение:
Корнем n-ой степени из неотрицательного числа а при четном n называют такое неотрицательное число, которое при возведении в степень n дает в результате число a.
Устная работа.
Вычислите: Решите уравнение:

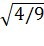 , , 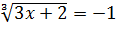
| ||||||||||
| Изучение нового материала |
Из определения следует важный вывод:
На множестве значений 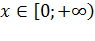 существует функция существует функция 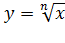 при n=2,3,4,… , т. е. при любом натуральном n, не равном единице.
Тогда как же выглядит график этой функции и, каковы ее свойства? Сегодня мы это узнаем.
Записываем тему урока: Функции при n=2,3,4,… , т. е. при любом натуральном n, не равном единице.
Тогда как же выглядит график этой функции и, каковы ее свойства? Сегодня мы это узнаем.
Записываем тему урока: Функции 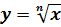 , их свойства и графики.
Начнем с известного вам случая, когда n=2, то есть с функции , их свойства и графики.
Начнем с известного вам случая, когда n=2, то есть с функции 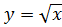 . Так как показатель степени четное число, то . Так как показатель степени четное число, то 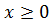 .
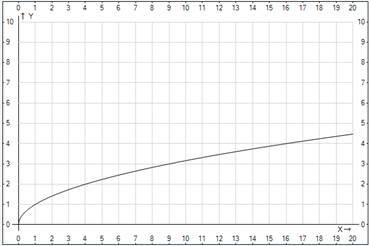
Изобразим график этой функции: .
Изобразим график этой функции:
Построим график функции
Как видно график обеих функций представляет собой ветвь параболы, только по-разному расположенную на координатной плоскости. Данные ветви парабол симметричны относительно прямой Значит график функции График функции |
Вывод: График функции при симметричен графику функции при относительно прямой .
Рассмотрим свойства функции 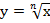 при
при 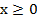 .
.
1. Область определения: 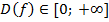 ;
;
2. Функция общего вида (не является четной либо нечетной);
3. Функция возрастает на луче 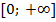 ;
;
4. Не ограничена сверху, но ограничена снизу;
5. Не имеет наибольшего значения, но имеет наименьшее значение 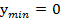 ;
;
6. Непрерывна;
7. Область значений: 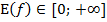 ;
;
8. Выпукла вверх на луче 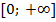 . Это означает, что мы можем взять произвольные точки А и В на графике, соединить их отрезком и содержащийся между этими точками кусок графика будет находиться над отрезком;
. Это означает, что мы можем взять произвольные точки А и В на графике, соединить их отрезком и содержащийся между этими точками кусок графика будет находиться над отрезком;
9. Функция дифференцируема в любой точке x>0. Функция имеет производную при любом х большем нуля; при 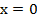 функция не имеет производной, касательной в этой точке является ось у.
функция не имеет производной, касательной в этой точке является ось у.
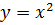 , при
, при 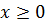 .
.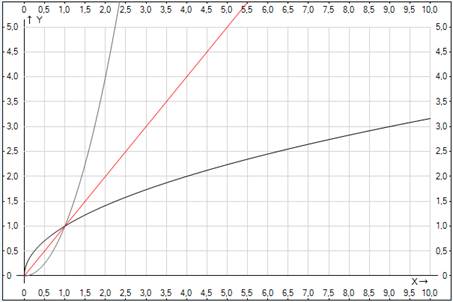
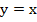 . графики имеют две общие точки: (0;0) и (1;1). На ветви параболы
. графики имеют две общие точки: (0;0) и (1;1). На ветви параболы 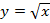 лежат точки с координатами
лежат точки с координатами 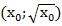 , на ветви параболы
, на ветви параболы 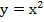 – точки с координатами
– точки с координатами 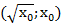 и наоборот. Эти точки симметричны относительно прямой
и наоборот. Эти точки симметричны относительно прямой 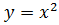 , при
, при 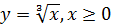 можно получить из графика функции
можно получить из графика функции 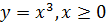 при помощи преобразовании симметрии относительно прямой y=x, и так далее.
при помощи преобразовании симметрии относительно прямой y=x, и так далее.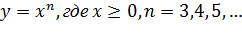 , напоминает по виду ветвь параболы. Чем больше n, тем круче эта ветвь устремляется вверх и тем ближе проходит к оси x в окрестности точки x=0.
, напоминает по виду ветвь параболы. Чем больше n, тем круче эта ветвь устремляется вверх и тем ближе проходит к оси x в окрестности точки x=0.