Контакты

Случайная статья

Контрольная работа № 2 по теме

25.11. Контрольная работа № 2 по теме

«Степень с натуральным показателем. Одночлены. Многочлены. Сложение и вычитание многочленов»

Решаем в течение урока (30-40 минут) и присылаем мне в личные сообщения ВК, кто зарегистрирован, или на почту bonavi69@mail.ru сегодня (25.11.) не позднее 16.00.

Решения записываем подробно: подобные подчеркиваем, действия с показателями степеней прописываем.

Вариант 1

(решают БарановаВ, Диков К, Камилов И, Левашова Я, Малов А, Мельникова А)

1. Представьте в виде степени: а) х² • х¹², б) а¹³: а⁷, в) (с⁵)³, г) y⁵ • (y⁵)², д) .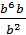

2. Упростите выражение:

а) –7х⁴у³ × 1,5х² × у⁴; б) (–3т⁴п⁷)³.

3. Выполните сложение и вычитание многочленов:

а) (7a – 9b)+( 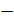4b+3a);

б) (–3x² – 5x+1) – (–4x² +x– 8).

4. Найдите значение выражения:

а) ; б) 1 – 12х² при х = – .

5. Решить уравнение: 7y³ – 5y = (y² – 2) – (8y + y² – 7y³)

Вариант 2

(решают Борягин И, Клюева В, Мельников Н, Мохова П, Нужная А, Пантюкова К)

1. Представьте в виде степени: а) c⁹ • c², б) b⁸: b⁴, в) (a⁵)³, г) x³ • (x⁴)³, д) .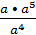

2.Упростите выражение:

а) 6b²с × (–2,5b⁵)∙ с³; б) (–3x¹¹у⁷)⁴.

3. Выполните сложение и вычитание многочленов:

а) (2a – 4b)+( 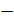5 a +2 b);

б) (–2x² – 4x+5) – (–3x² +7x– 8).

4. Найдите значение выражения:

а) ; б) 12х³ + 2 при х = – .

5. Решить уравнение: 27 – 3c⁴+ (2с² – 7с) = 2с² – (3c⁴+4с – 25)

Вариант 3

(решают ВоробьевА, Давлятов У, Зарубина М, Назеева С, Николаев К, Хапина А)

1. Выполните действия:

а) b⁸ × b¹⁵; б) b¹² : b⁴; в) (3b⁸)²; г)

2. Упростите выражение:

а) 3x⁵y³ × (–3,5xy⁷); б) (–2m⁶n⁹)⁵; в)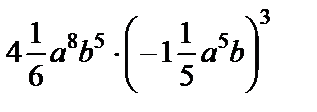

3. Выполните сложение и вычитание многочленов 10ab² + 8a²b+ аb и 8ab²–4аb.

4. Вычислите:

5. Упростите выражение: 12х²y+ y²– (10y²–(3х²y–( y²+2х²y)))

Вариант 4

(решают Баронова В, Батурина С, Коровина В, КуяноваВ, Сазанов Д, Третьяков Н, Шингова В)

1. Выполните действия:

а) с⁶ × с¹⁷; б) с²⁰ : с⁵; в) (2с⁷)⁴ ; г) .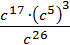

2. Упростите выражение:

а) –7a⁷b⁴ × 0,5ab²; б) (–2c⁸d¹²)³; в) .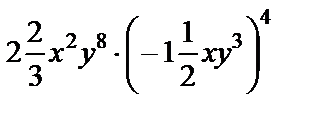

3. Выполните сложение и вычитание многочленов 13m²n + 5m³n²+ mn и 18 m³n²–3mn.

4. Вычислите: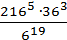

5. Упростите выражение: 2ab³+ a³– (ab³+(5a³–( 12ab³–a³)))

© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.