
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Группа 1БУ-67. Тема: Решение тригонометрических неравенств.. Пример 1
Группа 1БУ-67
Тема: Решение тригонометрических неравенств.
Задание:
1. Изучить теоретические сведения и законспектировать их.
2. Записать примеры выполнения заданий.
3. Выполнить задания.
4. Выполненные задания сфотографировать и отправлять на электронную почту tryufelka83@mail.ru или в ЛС https://vk.com/tryufelka83 социальной сети VKontakte.
5. Выполненные задания сдать до: 03.12.
Учебник: Алимов Ш.А. и др. Математика: алгебра и начала математического анализа, геометрия. Алгебра и начала математического анализа (базовый и углубленный уровни).10—11 классы. — М., 2014.
Ссылка на учебник онлайн:
https://uchebnik-skachatj-besplatno.com/Алгебра/Учебник%20Алгебра%2010-11%20класс%20Алимов%20Колягин/index.html#prettyPhoto
С. 194-196
Вспомним алгоритм решения простейших тригонометрических неравенств.
1) sinx ≥ - 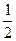 ;
;
 t1 < t2;
t1 < t2;
t1 = arcsin(- 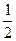 ) = -
) = - 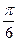 ;
;
t2 = p + 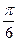 =
= 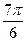 ;
;
- 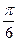 + 2pn ≤ х ≤
+ 2pn ≤ х ≤ 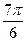 + 2pn, n Î Z.
+ 2pn, n Î Z.
| 2) cosx ≥ -
| t1 > t2; t1 = arccos(- = p - t2 = - -
| ||
| 3) cosx <
| t1 < t2;
t1 = arccos 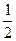 = = 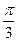 ;
t2 = 2p - ;
t2 = 2p - 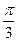 = = 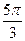 ; ;
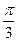 + 2pn < х < + 2pn < х < 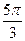 + 2pn, n Î Z. + 2pn, n Î Z.
| ||
4) sinx < 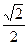 ; ;
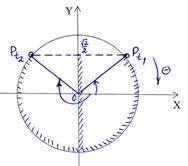
| t1 > t2; t1 = arcsin t2 = -p -
| ||
Теперь более сложные примеры.
Пример 1
Решим неравенство 
Обозначим аргумент косинуса 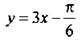 и получим простейшее тригонометрическое неравенство
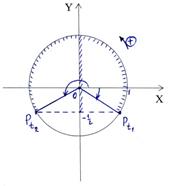
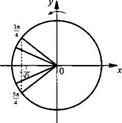
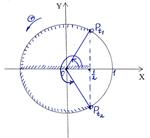
и получим простейшее тригонометрическое неравенство 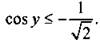 Решим это неравенство. На единичной окружности по оси абсцисс отложим значение
Решим это неравенство. На единичной окружности по оси абсцисс отложим значение 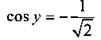 и построим соответствующие углы
и построим соответствующие углы 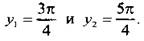 Тогда неравенству
Тогда неравенству 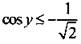 удовлетворяют значения
удовлетворяют значения 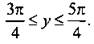 Учтем периодичность функции cos y и получим решения
Учтем периодичность функции cos y и получим решения 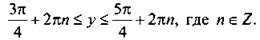
Теперь вернемся к старой неизвестной х и получим двойное линейное неравенство 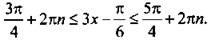 Ко всем частям неравенства прибавим число π/6. Отсюда
Ко всем частям неравенства прибавим число π/6. Отсюда 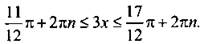 Все части неравенства разделим на положительное число 3. При этом знак неравенства сохраняется. Получим:
Все части неравенства разделим на положительное число 3. При этом знак неравенства сохраняется. Получим: 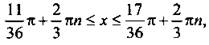 или
или 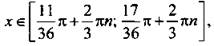 где n ∈ Z.
где n ∈ Z.
Если неравенство не является простейшим, то используя преобразования, аналогичные тем, которые применялись для уравнений, сводим неравенство к простейшему.
Пример 2. cos22x – 2cos2x ≥ 0.
(Вспомним прием решения тригонометрических уравнений вынесениемобщего множителя за скобку).
cos2x(cos2x – 2) ≥ 0.
Замена: cos2x = t, 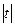 ≤ 1; t(t – 2) ≥ 0;
≤ 1; t(t – 2) ≥ 0; 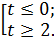 Второе неравенство не удовлетворяет условию
Второе неравенство не удовлетворяет условию 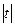 ≤ 1.
≤ 1.
cos2x ≤ 0. (Решить неравенство самостоятельно. Проверить ответ).
Ответ: 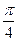 + pn < х <
+ pn < х < 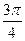 + pn, n Î Z.
+ pn, n Î Z.
Пример 3. 6sin2x – 5sinx + 1 ≥ 0.
(Вспомним прием решения тригонометрических уравнений заменой переменной).
Замена sinx = t, 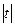 ≤ 1. 6t2 – 5t +1 ≥ 0, 6(t -
≤ 1. 6t2 – 5t +1 ≥ 0, 6(t - 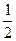 )(t -
)(t - 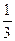 ),
), 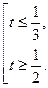
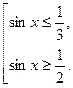
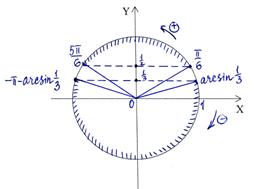
| 
|
Ответ: 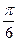 + 2pn ≤ х ≤
+ 2pn ≤ х ≤  + 2pn, -p-arcsin
+ 2pn, -p-arcsin 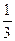 + 2pk ≤ х ≤ arcsin
+ 2pk ≤ х ≤ arcsin 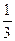 + 2pk,
+ 2pk,
n, k Î Z.
Домашнее задание.
№ 1415
№ 1417 (2)
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|
 ;
;
 ;
; + 2pn < х <
+ 2pn < х <