
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Компланарные векторы. Задание #1. Задание #2. Задание #3. Задание #4
Компланарные векторы
Задание #1
Вопрос: Укажите верные утверждения.
Выберите несколько из 4 вариантов ответа:
1) Векторы называются компланарными, если при откладывании их от одной и той же точки они будут лежать в одной плоскости.
2) Векторы называются компланарными, если имеются равные им векторы, лежащие в одной плоскости.
3) Векторы называются компланарными, если при откладывании их от одной и той же точки они не будут лежать в одной плоскости.
4) Векторы называются компланарными, если имеются равные им векторы, не лежащие в одной плоскости.
Задание #2
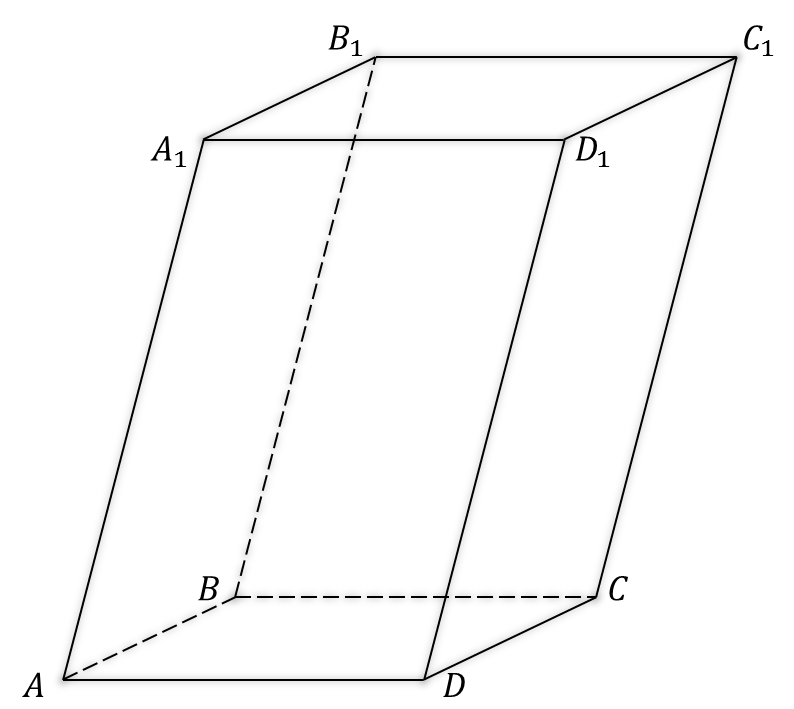
Вопрос: Пользуясь данными рисунка, укажите тройки компланарных векторов.
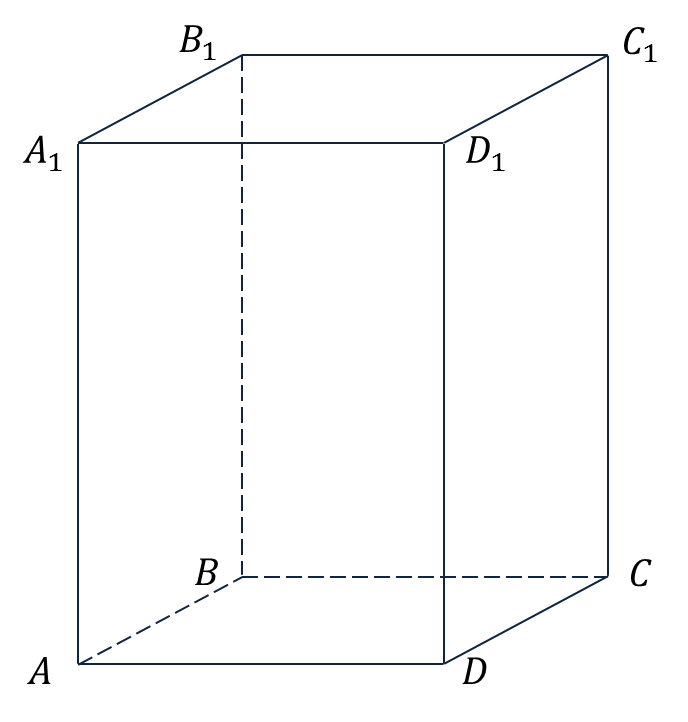 Изображение:
Изображение:
Выберите несколько из 4 вариантов ответа:
1) 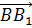 ,
, 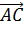 ,
, 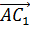 2)
2) 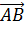 ,
,  ,
, 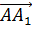
3) 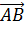 ,
, 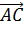 ,
, 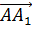 4)
4) 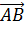 ,
, 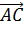 ,
, 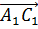
Задание #3
Вопрос: Известно, что векторы 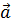 ,
, 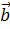 и
и 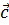 компланарны, а векторы
компланарны, а векторы 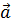 и
и 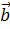 неколлинеарны. Какое из равенств будет тождественным для тройки векторов
неколлинеарны. Какое из равенств будет тождественным для тройки векторов 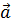 ,
, 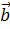 и
и 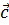 ?
?
Выберите один из 3 вариантов ответа:
1) 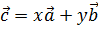 2)
2) 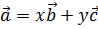 3)
3) 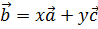
Задание #4
Вопрос: Укажите название теоремы: Если вектор  можно разложить по векторам
можно разложить по векторам 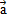 и
и  , то есть представить его в таком виде
, то есть представить его в таком виде  =x
=x 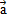 + y
+ y  , где x и y некоторые числа. То векторы
, где x и y некоторые числа. То векторы 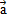 ,
,  и
и  компланарны.
компланарны.
Выберите один из 3 вариантов ответа:
1)признак компланарности трёх векторов
2) свойством трёх компланарных векторов
3) определение компланарных векторов
Задание #5
Вопрос: Укажите название теоремы: Если векторы 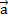 ,
,  и
и  компланарны, а векторы
компланарны, а векторы 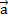 и
и  не коллинеарны, то вектор
не коллинеарны, то вектор  можно разложить по векторам
можно разложить по векторам 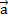 и
и  , причём коэффициенты разложения определяются единственным образом.
, причём коэффициенты разложения определяются единственным образом.
Выберите один из 3 вариантов ответа:
1)признак компланарности трёх векторов
2) свойством трёх компланарных векторов
3) определение компланарных векторов
Задание #6
Вопрос: Пользуясь данными рисунка, укажите тройки не компланарных векторов.
 Изображение:
Изображение:
Выберите несколько из 4 вариантов ответа:
1) 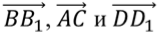 2)
2) 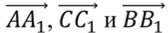
3) 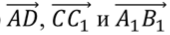 4)
4) 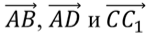
Задание #7
Вопрос:
Известно, что векторы 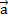 ,
,  и
и  компланарны. Тогда векторы 2
компланарны. Тогда векторы 2 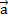 ,
,  +
+ 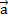 и
и 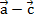 ….
….
Выберите один из 2 вариантов ответа:
1) компланарны 2) не компланарны
Задание #8
Вопрос: Точки А, В и С не лежат на одной прямой, а точка О не лежит в плоскости (АВС). Тогда векторы 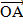 ,
, 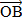 и
и 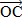 …
…
Выберите один из 2 вариантов ответа:
1) компланарны 2) не компланарны
Задание #9
Вопрос: Пользуясь данными рисунка, укажите являются ли векторы 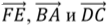 компланарными?
компланарными?
Изображение:
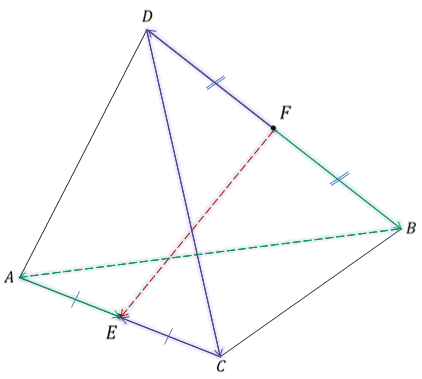
Выберите один из 2 вариантов ответа:
1) да 2) нет
Задание #10
Вопрос: Пользуясь данными рисунка Задания #9 , выразите вектор 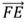 через векторы
через векторы 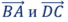 .
.
Выберите один из 3 вариантов ответа:
1) 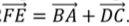 2)
2) 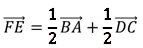 3)
3) 
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|