СОДЕРЖАНИЕ. Приложение

ГОСУДАРСТВЕННОЕ АВТОНОМНОЕ

ПРОФЕССИОНАЛЬНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ

СТЕРЛИТАМАКСКИЙ МНОГОПРОФИЛЬНЫЙ ПРОФЕССИОНАЛЬНЫЙ КОЛЛЕДЖ

(ГАПОУ СМПК)

КУРСОВАЯ РАБОТА

«РАЗРАБОТКА И РЕАЛИЗАЦИЯ ОКОННОГО ПРИЛОЖЕНИЯ «МАТЕМАТИЧЕСКАЯ ФОРМУЛА»»

Оценка: ______________ «___»_________ 2020 г.

Выполнила: студентка III курса группы ИСП-31 специальности 09.02.07 Информационные системы и программирование (программист) Куликова Екатерина Алексеевна. Руководитель: Борсук Артур Игоревич.

Стерлитамак, 2020

СОДЕРЖАНИЕ

АННОТАЦИЯ.. 3

ВВЕДЕНИЕ. 4

ГЛАВА I. ТЕОРЕТИЧЕСКИЕ ОСНОВЫ РЕАЛИЗАЦИИ ОКОНОГО ПРИЛОЖЕНИЯ «Разработка и реализация оконного приложения «Математические формулы». 6

1.1. Основные понятия по объекту и предмету проектирования. 6

1.2. Обзор подобных приложений. 14

ВЫВОДЫ ПО I ГЛАВЕ. 18

ГЛАВА II. ПРАКТИЧЕСКАЯ РАБОТА Разработка и реализация оконного приложения «Математические формулы». 19

2.1. Этапы реализации приложения. 19

2.2. Описание приложения и инструкция пользователя. 19

ВЫВОДЫ ПО II ГЛАВЕ. 19

ЗАКЛЮЧЕНИЕ. 19

СПИСОК ЛИТЕРА.. 20

ПРИЛОЖЕНИЕ

Замечания:

1. Параметры документа не соответствуют рекомендациям: левое поле.

2. Выравнивание по центру глав и пунктов ну никак не TABом делается.

3. В ведении не отражена значимость приложений. Большинство программ разрабатываются в виде приложений, которые направлены на решение различных прикладных задач пользователей. Приложения используются практически во всех сферах деятельности человека, от финансовых (заполнение деклараций) до образования… в этом ключе актуальность развивать нужно в первую очередь. Это как пример, написал коряво, указал только направление (ЭТО я уже писал кому-то, надеюсь у вас будет разными словами)

4. Задача 2 сформулирована не совсем верно: Рассмотреть понятие, виды, классификации, основные элементы приложений. Нужно примерно так поставить, что сможешь раскрыть из этого, то и оставишь, можно что-то свое добавить.

На будущее:

- глава II оформлена неверно

- оформление глав – не соответствует рекомендациям: 1,5 межстрочный интервал, прописные буквы

- вместо тире используешь дефис, проверь весь текст КР

- рисунки и названия рисунко в выравниваются по центру без красной строки

АННОТАЦИЯ

Объем курсовой работы – …стр.

Количество иллюстраций – … шт.

Количество таблиц – … шт.

Количество приложений – … шт.

Количество использованных источников – … шт.

Перечень ключевых слов: …

Полученные результаты: … .

ВВЕДЕНИЕ

Приложение может приниматься, как учебное пособие для учеников среднего и старшего звена, общеобразовательного учреждения и вузов. Для начала изучения учебного материала по алгебре, геометрии. Тема «Разработка и реализация оконного приложения «Математические формулы» может быть полезна для многим людей для расширения человеком познаний в математической и информационной сфере.

Обширная и интересная наука все развивается. Ученые веками изучали закономерности и выводили формулы, доказывали теоремы. Огромные труды, многовековые познания современные студенты должны освоить в короткий промежуток времени. Все осознают, что объять необъятные познания в области науки невозможно, поэтому курс математики и подразделов данной науки дает лишь поверхностное понимание законов и правил, лишь самые востребованные знания.

С первого класса и до конца жизни человек изучает формулы по математике, иногда даже не осознавая того. Их настолько много, что запомнить весь массив не удастся никогда. На выручку идут специальные сборники, классифицированные по различным характеристикам, в которых также нужно уметь ориентироваться. Применение правильной формулы дает простое решение задачи [7].

Современные научные издания математическими методами доказательство. Ученые вводят в текст большое число формул, символов. Отличительные особенности математических формул – большая смысловая концентрация, высокая степень абстрактности заключенного в них материала, специфичность математического языка. Математической формулой называется символическая запись какого-либо утверждения. Формулы помогают заменить в тексте сложные словесные выкладки, различные операции с количественными показателями. Существует мнение, что редактору, в котором много формул, намного проще, чем с текстом без формул. Это неверно, ибо формулы в еще большей степени, чем текст, могут претерпевать преобразования и иметь различные формы записи, причем для каждой конкретной формулы в каждом конкретном издании должен быть выбран оптимальный вид. При этом учитываются круг читателей, на который рассчитана данная книга, и особенности каждой формулы, чтобы избежать ошибок, неясностей или неудобочитаемости [6].

Цель проекта: разработать и реализовать оконное приложение «Математические формулы».

Объект проекта: реализация оконного приложения.

Предмет проекта: оконное приложение как средство изложения материала «Математические формулы».

Задачи проекта:

1. Рассмотреть учебную и учебно-техническую литературу по теме курсовой работы.

2. Описать основные понятия, что такое оконное приложение, математические формулы.

3. Выполнить обзор оконных приложений подобного содержания.

4. Разработать техническое задание по реализации приложения «Математические формулы».

5. Описать этапы проектирования оконного приложения «Математические формулы».

Программные средства: Microsoft Visual Studio.

Область применения: образование.

Целевая аудитория: приложение рассчитано на учеников среднего и старшего звена, учащихся СПО и студентов ВУЗов.

ГЛАВА I. ТЕОРЕТИЧЕСКИЕ ОСНОВЫ РЕАЛИЗАЦИИ ОКОНОГО ПРИЛОЖЕНИЯ «Разработка и реализация оконного приложения «Математические формулы»

1.1. Основные понятия по объекту и предмету проектирования

Оконное приложение - основное понятие оконного интерфейса, интерфейсный контейнер. Кроме дочерних элементов интерфейса, окно также может содержать элементы управления самим окном. Важная особенность окон – возможность перекрываться, то есть располагаться поверх друг друга, полностью или частично закрывая нижнее окно.

Впервые концепцию перекрывающихся окон, как и многие другие концепции пользовательских интерфейсов, разработали в исследовательском центре Xerox PARC для системы Xerox Alto, а точнее для среды разработки языка smalltalk в 1974 году. В этой среде у окон уже были границы и заголовки, но ещё не появилось кнопок управления окнами. Дальнейшее развитие оконный интерфейс получил в среде Xerox Star, но первым коммерчески успешным компьютером, использующим, окна стал вышедший в 1984 году Apple Macintosh [2].

Оконные приложения строятся по принципам событийно-управляемого программирования (event-driven programming) - стиля программирования, при котором поведение компонента системы определяется набором возможных внешних событий и ответных реакций компонента на них. Такими компонентами в Windows являются окна. С каждым окном в Windows связана определенная функция обработки событий - оконная функция. События для окон называются сообщениями. Сообщение относится к тому или иному типу, идентифицируемому определенным кодом, и сопровождается парой 32-битных параметров, интерпретация которых зависит от типа сообщения. Задача любого оконного приложения - создать главное окно и сообщить Windows функцию обработки событий для окна. Все самое интересное для приложения будет происходить именно в функции обработки событий главного окна. В Windows программа пассивная. После запуска она ждет, когда ей уделит внимание операционная система. Операционная система делает это посылкой сообщений. Сообщения могут быть разного типа, они функционируют в системе достаточно хаотично, и приложение не знает, какого типа сообщение придет следующим. Логика построения Windows-приложения должна обеспечивать корректную и предсказуемую работу при поступлении сообщений любого типа.
Классическое оконное приложение, как правило, состоит по крайней мере из двух функций:

1. стартовая функция, создающая главное окно WinMain ();

2. функция обработки сообщений окна (оконная функция).

Существует два вида оконных приложений:

1. Консольное приложение – это программа, которая работает с командной строкой. То есть это обычное окно, где пользователь может вести какую-то команду и получить результат. Пример консольного приложения – это командный интерпретатор, который есть в любой оперативной системе. В Windows 95/98/ME – это программа command.com. В Windows 2020 и выше - это программа cmd.exe;

2. Оконное приложение - это привычная всем программа Windows. То если это окошко кнопочками и полями для ввода-вывода данных. На сегодняшний день это, пожалуй, самый распространенный вид программ. Именно оконного приложения создают большинство программистов [3]. Windows поддерживает два типа приложений: основанные на графическом интерфейсе (graphical user interface, GUI) и консольные (console user interface, CUI). В приложениях первого типа внешний интерфейс чисто графический GUI-приложения создают окна, имеют меню, взаимодействуют с пользователем через диалоговые окна и вообще пользуются всей стандартной «Windows'oвской» начинкой. Почти все стандартные программы Windows — Notepad, Calculator, Wordpad и другие - являются GUI-приложениями. Приложения консольного типа работают в текстовом режиме: они не формируют окна, не обрабатывают сообщения и не требуют GUI. И хотя консольные приложения на экране тоже размещаются в окне, в нем содержится только текст. Командные процессоры вроде Cmd.exe (в Windows 2000) или Command.com (в Windows 98) - типичные образцы подобных приложений [4].

Математика – наука, которая кажется незаметной, но она сопровождает нас всю сознательную жизнь. С числами и формулами нас знакомят в школе, а жизнь находит применение базовым знаниям.

Математические формулы - в математике, а также физике и прикладных науках, символическая запись высказывания, либо формы высказывания. Формула, наряду с термами, является разновидностью выражения формализованного языка. В более широком смысле формула - всякая чисто символьная запись, противопоставляемая в математике различным выразительным способам, имеющим геометрическую коннотацию: чертежам, графикам, диаграммам, графам.

История математических обозначений - история разработки символов, используемых для компактной записи математических уравнений и формул. Помимо индо - арабских цифр и букв различных алфавитов, математический язык использует множество специальных символов, изобретённых за последние несколько столетий.

Хорошо продуманные обозначения, отражающие свойства изучаемых объектов, помогают избежать ошибок или неправильной трактовки, переносят часть исследования на технический уровень, нередко «подсказывают» правильный путь к решению задачи. По словам Альфреда Уайтхеда, удачное обозначение освобождает мозг от ненужной работы, тем самым позволяя ему сосредоточиться на более важных задачах.

Первоначально математические утверждения формулировались словесно. Такая запись была громоздкой, часто неоднозначной, а алгебраические обрела собственный язык, не требующий перевода, язык с чётко определённым смыслом «слов» и строгой грамматикой, позволяющий выводить из истинных утверждений другие, столь же истинные.

Уравнение - формула, внешняя (верхняя) связка которого представляет собой бинарное отношение равенства. Однако важная особенность уравнения заключается также в том, что входящие в него символы делятся на переменные и параметры.

Тождество - суждение, верное при любых значениях переменных. Под тождеством подразумевают тождественно верное равенство, хотя снаружи тождества может стоять и неравенство или какое-либо другое отношение. Во многих случаях тождество можно понимать, как некое свойство используемых в нём операций, тождество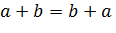

Утверждает коммутативность сложения.

Сложение и вычитание - используются знаки «+» и «−» (последний на письме довольно слабо отличим от дефиса). Унарный минус чаще используется лишь при первом (левом) слагаемом, поскольку другие случаи, типа «a + (−b)» и «a − (−b)», ничем не отличаются по смыслу от более простых «a − b» и «a + b» соответственно [1].

Типы математических формул:

1. Формулы сокращенного умножения:

I. квадрат суммы: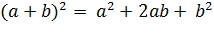

II. разность квадратов: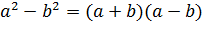

2. Свойства степеней и корней:

I. основные свойства степеней: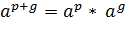

II. Основные свойства математических корней: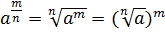

3. Арифметическая прогрессия:

I. Формула n-го члена арифметической прогрессии: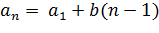

II. Соотношение между тремя соседними членами арифметической прогрессии: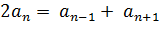

4. Геометрическая прогрессия:

I. Формула n-го члена геометрической прогрессии: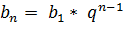

II. Свойства геометрической прогрессии: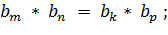

при: m + n = k + p.

5. Тригонометрия:

I. Определение синуса: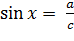

II. Определение косинуса: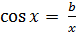

6. Формула двойного угла:

I. Синус двойного угла: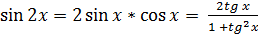

7. Тригонометрические формулы сложения:

I. Синус суммы/разности: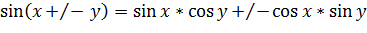

II. Тангенс суммы/разности: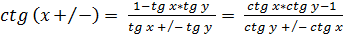

8. Тригонометрические формулы преобразования в сумму:

I. Произведение синусов: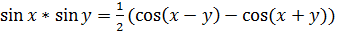

II. Произведение синусов и косинусов: 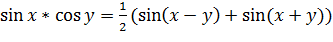[5].

Математические формулы в процессе эволюции своего назначения претерпевали изменения, и связано это было с изменением понимания назначения самих формул. Числа давно уже перестали быть просто числами, а стали делиться на элиту в виде простых чисел, и на все остальные цифры. Когда любое число стало возможным представить в виде двух простых, а их, в свою очередь, представить кодированными символами, то и методы действий над ними тоже немного изменились. Не секрет, что каждый человек, работающий в сфере чисел, имеет свои наработки и взгляды на алгебраические формулировки. Суть в том, что как раз из этого и возникают предпосылки к возникновению новых формул и трактовок к их пониманию. Как бы ни были нам в прошлом дики массивы чисел, и массивы массивов только помогают в развитии других аспектов математических формул.

Современные научные издания насыщены математическими методами доказательств. Ученые вводят в текст большое число формул, символов. Отличительные особенности математических формул – большая смысловая концентрация, высокая степень абстрактности заключенного в них материала, специфичность математического языка. Это в известной степени осложняет восприятие читателем текста и ставит перед редактором немало проблем.

Математической формулой называется символическая запись какого-либо утверждения (предложения, суждения). Формулы помогают заменить в тексте сложные словесные выкладки, различные операции с количественными показателями. Для этого используют специальные обозначения – символы, которые можно разделить на три группы:

– условные буквенные обозначения математических и физико-технических величин;

– условные обозначения единиц измерения величин;

– математические знаки.

Существует мнение, что редактору работать с текстом, в котором много формул, намного проще, чем с текстом без формул. Это неверно, ибо формулы в еще большей степени, чем текст, могут претерпевать преобразования и иметь различные формы записи, причем для каждой конкретной формулы в каждом конкретном издании должен быть выбран оптимальный вид. При этом учитываются круг читателей, на который рассчитана данная книга, и особенности каждой формулы, чтобы избежать ошибок, неясностей или неудобочитаемости. В учебнике для школьников, учащихся ПТУ эта формула должна иметь другой вид.

Эксплуатационная скорость, которую принято обозначать характеризует условную среднюю скорость подвижного состава за все время пребывания его в наряде (на работе) и определяется отношением пробега ко времени в наряде.

При прочих равных условиях предпочтение следует отдавать таким символам в формулах, которые легко и однозначно воспроизводятся на письме (от руки). В первую очередь это относится к учебникам, формулы из которых преподаватель пишет на доске, учащийся – в конспекте и т.д. Трудности здесь возникают обычно в связи со сходным начертанием букв разных алфавитов и из-за неоправданной усложненности индексов. Так, Rг.ц легко и записать, и потом прочитать. А теперь попытаемся прочитать запись? e.g. Для этой, казалось бы, выразительной записи существуют свыше 100 (!) вариантов прочтения, ибо есть шесть вариантов для с («ро» строчная и прописная; «пэ» строчная и прописная; «эр» строчная и прописная); четыре варианта для е («е» и «эль», на строке и в индексе); шесть вариантов для g («дэ» и «жэ»; на строке, в индексах первой и второй ступени). Кроме того, всю запись можно прочитать и как «? логарифмическое».

Формула должна иметь хороший графический рисунок. Плохо воспринимаются, например, цифры в середине сомножителей (их лучше ставить спереди), сложные показатели степени и индексы, многоступенчатые индексы, сложные формулы, приведенные к компактному виду.

Особой разновидностью искажений графики, еще больше ухудшающих «внешний вид» формулы, являются нарушения правил набора. Желая упростить его, иногда смещают верхние индексы относительно нижних (K^ав_ткм). Точки в индексах часто оказываются не на месте и выглядят знаком умножения (Д_Б_.П). Запятые после формул неопытные наборщики набирают в индексах (А =ВС_к). Не соблюдаются правила выбора кегля для подключек, в результате чего формула и экспликация становятся не похожими друг на друга. Если в индексах встречаются буквы разных алфавитов, часто они плохо выравниваются («пляшут»). Знак деления «косая черта» по высоте часто ниже (меньше кегль) делимого и делителя. Из сказанного можно сформулировать рекомендации по улучшению воспроизводимости и графики формул.

Что касается главного условия хорошей воспринимаемости формул – облегчения их понимания и запоминания, – необходимо учитывать следующие рекомендации:

– при прочих равных условиях русские символы, являющиеся первой буквой зашифрованного слова, воспринимаются, т.е. понимаются и запоминаются, лучше, чем латинские или греческие;

– в качестве символов нежелательно использовать аббревиатуры, так как они воспринимаются как произведение;

– индекс по возможности должен яснее отражать зашифрованное в нем слово или словосочетание;

—легко понимается и запоминается формула, в которой наглядно отражена зависимость результата вычисления от характера изменения параметров.

Единицы физических величин следует помещать только после подстановки в формулу числовых значений величин и проведения промежуточных вычислений – при получении конечного результата.

Чтобы сделать трудоемкость редактирования минимальной, надо добиться того, чтобы авторы представляли материал, в кото–ром соблюдены следующие требования:

– формулы вписаны от руки печатными буквами, аккуратно и ясно (если автор не смог осуществить компьютерный набор);

– знаки деления в сложных формулах имеют вид горизонталь–ной черты. Такие формулы легко проверить, проанализировать и принять решение, согласовав, естественно, с автором целесо–образность придания формуле более компактного вида;

– сделаны необходимые уточнения на полях («е» – не «эль» и т.д.);

– число букв и знаков, требующих дополнительного разъясне–ния на полях, сведено в формулах к минимуму [6].

1.2. Обзор подобных приложений

Рисунок 1. Логотип Geogebra Classic

Приложение Geogebra Classic - это кроссплатформенная динамическая математическая программа для всех уровней образования, включающая в себя геометрию, алгебру, таблицы, графы, статистику и арифметику.

Программа написана Маркусом Хохенвартером на языке JAVA и работает на большом числе операционных систем. Переведена на 39 языков.

Программа позволяет создавать Java-апплеты динамических чертежей для их включения в Веб-страницы.

Положительные стороны программы «Geogebra Classic»:

1) Оптимизировать учебный процесс, более рационально используя время на различных этапах урока.

2) Способствует развитию познавательной активности учащихся.

3) Позволяет быстрее и эффективнее освоить школьный курс по математике, повышает запоминаемость материала. [8].

Отрицательные стороны программы:

1) Большинство проектов выкладываются на английском языке.

Программа не подходит для школьной программы, так как может создавать достаточно продвинутые графики функций. GeoGebra больше подходит для преподавателей ВУЗов, в качестве программы для наглядной демонстрации. [9].

Рисунок 2. Логотип MathType

Приложение MathType – это проприетарное прикладное программное обеспечение, созданное Design Science представляющее собой интерактивный редактор формул для Microsoft Windows и Macintosh, который позволяет создавать математические записи для текстовых процессоров.

Однако, существуют значительные проблемы с совместимостью с Adobe Acrobat и созданием PDF файлов из документов, содержащих элементы MathType. [10].

Строка меню имеет следующие компоненты: File (Файл); Edit (Правка); View (Вид); Forma (Формат); Style (Стиль); Size (Размер); Preferences (Настройки); Help (Помощь); Window (для системы Mac).

Строка состояния выполняет две функции:
1) Показывает настройки, сделанные с использованием команд различных меню – Format (Формат), Style (Стиль), Size (Размер).
2) Позволяет непосредственно сделать необходимые настройки.

Style - Выбор и настройка стилей; Size - Настройки размеров; Zoom - Выбор масштаба; Color - Выбор цвета.

Вы можете использовать линейку при создании формул.
Для этого в меню View (Вид) выберите Ruler (Линейка) - Ctrl + Alt+R / ⌘ + ⌥ + R Флажок рядом с этим пунктом меню указывает, что линейка отображается в данный момент.

Toolbar size - Размер панели инструментов

Ruler units - Единицы измерения линейки - единицы измерения интервалов для знаков градации, отображаемых на линейке, в дюймах, сантиметрах, точках или picas.

User interface language - Язык пользовательского интерфейса.

Spaces - Пробелы. Цвет по умолчанию серый. Кнопка "Change", чтобы изменить цвет фона.

Custom Speech text Пользовательский текст речи (только для Windows).
Снова показать все учебные сообщения, иногда появляется одноразовое сообщение, объясняющее различные функции MathType Desktop. Их можно отключить в диалоговом окне сообщения. [11].

Положительные и отрицательные стороны приложения инсталлировать данный софт можно абсолютно на все операционные системы Windows. утилита может совместно работать с большим количеством приложений и сайтов. Помимо этого, после окончания пробного периода можно работать в режиме Lite.

Из негативных моментов стоит выделить работоспособность пробной версии всего один месяц. Кроме того, иногда могут возникать проблемы с совместимостью с Adobe Acrobat.

Установив это приложение, пользователь может комфортно работать с математическими выражениями. При этом рекомендуется запустить защитные средства ПК, которые будут блокировать попадание вирусов и вредоносов в операционную систему. [12].

Рисунок 3. Логотип Mathcad

Приложение Mathcad система компьютерной алгебры из класса систем автоматизированного проектирования, ориентированная на подготовку интерактивных документов с вычислениями и визуальным сопровождением, отличается лёгкостью использования и применения для коллективной работы.

Mathcad был задуман и первоначально написан Алленом Раздовом [2] из Массачусетского технологического института (MIT), соучредителем компании Mathsoft, которая с 2006 года является частью корпорации PTC (Parametric Technology Corporation).

Mathcad также используется в сложных проектах, чтобы визуализировать результаты математического моделирования путём использования распределённых вычислений и традиционных языков программирования [3].

Открытая архитектура приложения в сочетании с поддержкой технологий .NET и XML позволяют легко интегрировать Mathcad практически в любые ИТ-структуры и инженерные приложения.

Программа позволяет выполнять численные и символьные вычисления, производить операции со скалярными величинами, векторами и матрицами, автоматически переводить одни единицы измерения в другие.

Среди возможностей Mathcad можно выделить:

1. Решение дифференциальных уравнений, в том числе и численными методами

2. Построение двумерных и трёхмерных графиков функций (в разных системах координат, контурные, векторные и т. д.)

Основное отличие Mathcad графический, а не текстовый режим ввода выражений. Для набора команд, функций, формул можно использовать как клавиатуру, так и кнопки на многочисленных специальных панелях инструментов. Пользователя: или мгновенно, одновременно с набором, либо по команде. Любые переменные, формулы, параметры можно изменять, наблюдая воочию соответствующие изменения результата.

Mathcad имеет недостатки невозможность построения поверхностей, заданных параметрически, с непрямоугольной областью определения двух параметров; создание и форматирование графиков только через меню, что ограничивает возможности программного управления параметрами графики. Расширение функциональности возможно дополнение Mathcad новыми возможностями с помощью специализированных пакетов расширений и библиотек, которые пополняют систему дополнительными функциями [13].

ВЫВОДЫ ПО I ГЛАВЕ

В данной главе рассмотрены такие основные определения, как математика и математические формулы. Также была приведен обзор приложений, которые могут приниматься, как учебное пособие для учеников среднего и старшего звена, общеобразовательного учреждения и вузов.

Математика, математические формулы – наука, которая кажется незаметной, но она сопровождает нас всю сознательную жизнь. В более широком смысле формула - всякая чисто символьная запись, противопоставляемая в математике различным выразительным способам, имеющим геометрическую коннотацию: чертежам, графикам, диаграммам, графам.

Исходя из рассмотренной литературы, математики можно классифицировать по таким типам как математические формулы, откуда они берутся и к чему и где их можно принимать. У каждого типа есть свои определенные задачи, влияющие состояние программы.

Рассмотрено понятие «математические формулы», в более широком смысле формула - всякая чисто символьная запись, противопоставляемая в математике различным выразительным способам, имеющим геометрическую коннотацию: чертежам, графикам, диаграммам, графам.

Такие программы стремятся к максимальному удобству для пользователя, что делает доступным для использования программы в любом месте и в любое время на любых устройствах.

Был проведен сравнительный анализ информационных приложений, используя критерии WorldSkills. Критерии состояли из модулей. Модуль посвящен описанию и понятиям о математике, математических формул, и что такое оконное приложение. По данным критериям был произведен анализ трех прилжений: «Geogebra Classic», «MathType» и «Mathcad». При анализе каждого сайта были представлены скриншоты сайтов, с целью подтверждения выполнения критерия.

ГЛАВА II. ПРАКТИЧЕСКАЯ РАБОТА Разработка и реализация оконного приложения «Математические формулы»

2.1. Этапы реализации приложения

Раскрыть содержание основных этапов проектирования/ разработки/ реализации приложения в соответствии с техническим заданием.

2.2. Описание приложения и инструкция пользователя

Содержит описание и назначение основных компонентов приложения, сопровождаемые комментариями и «скриншотами».

Приводится описание инструкции по работе пользователя с приложением.

ВЫВОДЫ ПО II ГЛАВЕ

Перечисляются основные, ключевые моменты, рассмотренные в практической части.

ЗАКЛЮЧЕНИЕ

Должно содержать краткие выводы по результатам выполнения КР, оценку полноты реализации поставленных задач.

Все задачи, поставленные во введении должны найти отражение в заключении.

Объем заключения не должен превышать 2-3 страниц.

СПИСОК ЛИТЕРА

Приложение